
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи математической статистики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия математической статистики. При проведении медико-биологических экспериментов исследователя обычно интересует какой-либо количественный или качественный признак у ряда особей, составляющих данную популяцию. В результате таких опытов исследователь получает ряд отличающихся друг от друга и в то же время сходных в некоторых существенных отношениях объектов. Этот ряд, лучше назвать его множеством, есть совокупность. Серия наблюдений или измерений есть совокупность. Объем совокупности – это число единиц совокупности. Его принято обозначать N. Следует заметить, что в некоторых программах, например, в EXCEL, вместо объема используется понятие размер. Отдельные члены совокупности называются вариантами (от латинского variance, variantis – различимый, изменяющийся). Совокупность всех объектов, для которой имеется типичная характеристика или признак, называется генеральной совокупностью. Это теоретически бесконечно большая (N аҐ) совокупность. Ясно, что генеральную совокупность изучить невозможно. На практике исследователь имеет дело с выборочными совокупностями или просто выборками. Можно сказать, что множество объектов – это генеральная совокупность, его подмножество – выборочная совокупность. Статистические показатели выборочной совокупности. Графики вариационных рядов (гистограммы) - это как бы «сгущение исходного материала», его наглядная картина. Но для сравнения разных выборок нужны количественные показатели. Существует два таких показателя (на самом деле две группы), но для простоты мы рассмотрим только основные. Вариационные ряды (выборки) могут различаться: ¨ по значению признака, вокруг которого концентрируется большинство вариант, то есть среднее арифметическое; ¨ по степени отклонения от среднего показателя, то есть вариационный размах, среднеквадратичное отклонение, или дисперсия. Остановимся подробнее на обсуждении этих величин. Среднее арифметическое
О величине среднего арифметического уже много было сказано в предыдущих главах. Что нового можно добавить с точки зрения биологической статистики? Среднее арифметическое является обобщающей величиной, которая как бы впитывает в себя все особенности данной совокупности или ряда. Величина
Математическое ожидание В биологических исследованиях может представлять известный интерес среднее геометрическое:
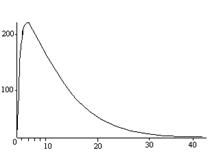
Пример. Пусть, например, необходимо вычислить средний за год ежемесячный темп прибавки веса грудного ребенка по результатам измерения относительного увеличения веса за каждый месяц. · за 1-й месяц - в 1,23 раза; · за 2-й месяц - в 1,19 раза; · за 3-й месяц - в 1,2 раза и т.д. В этом случае более адекватным выражением среднемесячного темпа привеса будет не среднее арифметическое, а среднее геометрическое значение. Для характеристики абсолютного увеличения веса более адекватным будет среднее арифметическое. Мода -это еще одна характеристика положения распределения. В тех выборочных совокупностях, где может быть произведена только классификация вариант по какому-нибудь качественному признаку, наиболее типичную группу, в которую входит больше всего вариант, называют модой. Можно использовать эту характеристику и для количественных оценок. На рисунке изображено распределение по возрасту заболевших дифтерией. Очевидно, что знание среднего возраста заболевших менее интересно, чем знание возраста, в котором чаще всего происходит заболевание (от 2 до 4 лет). В частности, при решении вопроса о том, где должны быть сосредоточены главные профилактические усилия: в школах или в дошкольных учреждениях.
Если же распределение более или менее симметрично, то мода и среднее арифметическое значение близки друг к другу. Дисперсия Однако, знания только среднего арифметического еще недостаточно для характеристики совокупности, так как главной особенностью совокупности является наличие разнообразия между ее членами, то есть вариации. Характеристикой вариации является средний квадрат отклонений
Для генеральной совокупности
а среднеквадратичное отклонение s, соответственно:
Для выборочной совокупности формулы отличаются. Обратите внимание, в знаменателе вместо
Чем объяснить такое различие формул? Для ответа на этот вопрос нужно познакомиться с таким понятием как число степеней свободы. Числом степеней свободы называется число независимых переменных (вариант) минус число наложенных связей (ограничений). Число степеней свободы принято обозначать либо df (degrees of freedom), либо n (греческая буква ню). Если изучаемая совокупность состоит из трех вариант, то при расчете среднего арифметического А теперь рассмотрим ситуацию, когда по какой-то причине эти три числа (варианты) должны быть такими, чтобы их сумма была равна заданному числу, например, 300. Тогда из исходных трех вариант только 2 могут быть любыми по величине. Что же до третьей варианты, она выбирается равной
Распределение Стьюдента.
Нормальное распределение достаточно хорошо описывает поведение непрерывной случайной величины не только при Для таких ситуаций было предложено распределение случайной величины
Результат был указан в 1908 году английским исследователем Вильямом Госсетом, опубликовавшим свою работу под псевдонимом Стьюдент, но строго был получен З.Фишером в 1925 году. По виду эта формула напоминает выражение для нормированной случайной величины
Однако, между ними весьма существенная разница. В числителе вместо индивидуальных значений Х стоит выборочное среднее арифметическое, а в знаменателе вместо среднеквадратичного отклонения генеральной совокупности s стоит ошибка среднего арифметического для выборки. Плотность вероятности случайной величины
где BN зависит от объема выборки. При малых значениях N кривая плотности вероятности Практическим следствием открытия закона распределения Стьюдента явилось изменение формул, определяющих границы доверительного интервала для математического ожидания случайной величины при заданной доверительной вероятности РD. Доверительный интервал должен вычисляться по формуле:
Сравним значения доверительных интервалов в случае распределения Гаусса и распределения Стьюдента для одной и той же доверительной вероятности:
Через Исследования Стьюдента сыграли громадную роль, так как дали возможность работать с малыми выборками. Обратим еще раз ваше внимание на то, что главная задача, которую решает математическая статистика (ради чего, собственно говоря, эта наука и существует), заключается в том, чтобы на основании изучения выборки делать выводы о свойствах генеральной совокупности. Выборка - это лишь часть генеральной совокупности. Типы ошибок. Ошибки измерения принято подразделять на систематические и случайные. Систематические ошибки вызываются факторами, действующими одинаковым образом при многократном повторении измерений, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов, и поэтому они сохраняют свою величину и знак от измерения к измерению. Случайные ошибки обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. То есть даже для измерений, выполненных одинаковым образом, величина и знак случайной ошибки изменяются от измерения к измерению. Встречается еще один тип ошибок - это грубые ошибки, или промахи. Источником их является недостаток внимания экспериментатора. Для устранения промахов нужно соблюдать аккуратность и тщательность в работе и записях результатов.
Основные понятия математической статистики. При проведении медико-биологических экспериментов исследователя обычно интересует какой-либо количественный или качественный признак у ряда особей, составляющих данную популяцию. В результате таких опытов исследователь получает ряд отличающихся друг от друга и в то же время сходных в некоторых существенных отношениях объектов. Этот ряд, лучше назвать его множеством, есть совокупность. Серия наблюдений или измерений есть совокупность. Объем совокупности – это число единиц совокупности. Его принято обозначать N. Следует заметить, что в некоторых программах, например, в EXCEL, вместо объема используется понятие размер. Отдельные члены совокупности называются вариантами (от латинского variance, variantis – различимый, изменяющийся). Совокупность всех объектов, для которой имеется типичная характеристика или признак, называется генеральной совокупностью. Это теоретически бесконечно большая (N аҐ) совокупность. Ясно, что генеральную совокупность изучить невозможно. На практике исследователь имеет дело с выборочными совокупностями или просто выборками. Можно сказать, что множество объектов – это генеральная совокупность, его подмножество – выборочная совокупность.
Основные задачи математической статистики. Статистику можно рассматривать как: · учение о совокупностях; · учение о вариациях; · учение о методах приведения данных к компактной форме. Задачи, возникающие в связи с анализом результатов наблюдений, можно подразделить на три типа: 1) Проблема спецификации, которая состоит в выборе математической формы генеральной совокупности. 2) После того, как задача спецификации решена, возникает проблема оценки. Она заключается в том, что следует установить способ вычисления по данной выборке статистики, пригодной для оценки неизвестного параметра генеральной совокупности. 3) Проблема распределения состоит в выводе точной математической формы распределения наших оценок в случайных выборках и в определении других статистик, предназначенных для проверки пригодности приведенной ранее спецификации (критерии согласия). Таким образом, статистическая обработка некоторой массы наблюдений логически содержит в себе то же чередование индуктивного и дедуктивного методов, которые вообще свойственны науке. Сначала со всей тщательностью формулируется некоторая гипотеза; из нее дедуктивным путем выводятся логические следствия; эти следствия сравниваются с надлежащими наблюдениями. Если эти последние находятся в полном соответствии с дедуктивными выводами, то гипотеза считается подтвержденной, по крайней мере до тех пор, пока не будут получены новые и более точные данные.Наличие в приведенной выше общей схеме статистического исследования дедуктивных выводов, относящихся к выборкам и покоящихся на допущении существования генеральной совокупности, из которой эти выборки взяты, определяет собой то особое положение, которое занимает в статистике классическая теория вероятностей. Если дана некоторая генеральная совокупность, то мы имеем возможность определить вероятность появления данной выборки и вместе с этим вероятность (если эта задача имеет более или менее простое математическое решение) появления данного значения статистики, исчисленной по этой выборке. Указанная выше проблема распределения может рассматриваться как приложение и соответствующее развитие теории вероятностей. 4.3 Схема предварительной обработки экспериментальных данных. Исходный числовой материал или совокупность полученных на опыте значений случайной величины
Для определения значения · · · Длина малого интервала рассчитывается по формуле:
Затем составляется таблица распределения, точнее закон распределения случайной величины
Здесь Dxk - На базе интервальной таблицы может быть построена гистограмма, то есть закон распределения может быть представлен в виде графика. Примечание: При группировке вариант следует обратить внимание на следующее: 1. начало первого интервала не обязательно должно быть равно 2. длина интервала должна оставаться постоянной; 3. одна и та же величина не должна встречаться дважды, то есть, если некоторое значение попадает на границу интервала, то учитывать его следует только для одного интервала, либо для i-того, либо для (i+1)-го интервала. При анализе графиков вариационных рядов (гистограмм) выявляются следующие закономерности: · большинство вариант располагается около середины вариационной кривой, образуя максимум; · распределение вариант в обе стороны от максимума кривой более или менее симметрично; · частота вариант постепенно убывает к краям вариационного ряда. Перечисленные закономерности есть не что иное, как закономерности случайной величины, рассмотренной в предыдущей главе (см., например, нормальное распределение). Далее следует переходить к оценке количественных характеристик выборочной совокупности, а именно статистических показателей.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 801; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.131 (0.013 с.) |

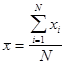 .
. дает сводную обощенную характеристику данного изучаемого признака.
дает сводную обощенную характеристику данного изучаемого признака. - есть характеристика генеральной совокупности (
- есть характеристика генеральной совокупности (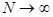 ), то есть то значение случайной величины, которое близко к истинному. Выборочное значение
), то есть то значение случайной величины, которое близко к истинному. Выборочное значение 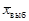 , то есть полученное по результатам выборки не равно математическому ожиданию, но чем больше объем выборки (
, то есть полученное по результатам выборки не равно математическому ожиданию, но чем больше объем выборки ( ), тем меньше отклонение
), тем меньше отклонение 
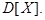
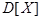 (или дисперсия),
(или дисперсия),  .
.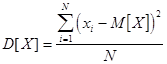 ,
,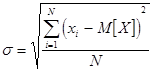 .
.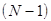 , вместо математического ожидания
, вместо математического ожидания 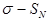 (оценка среднеквадратичного отклонения для выборки).
(оценка среднеквадратичного отклонения для выборки).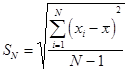
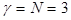 , так как никаких ограничений в данной ситуации не налагается.
, так как никаких ограничений в данной ситуации не налагается. . То есть в данном опыте накладывается одно ограничение и число степеней свободы будет
. То есть в данном опыте накладывается одно ограничение и число степеней свободы будет 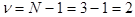 . С похожим ограничением мы сталкиваемся при расчете дисперсии или среднеквадратичного отклонения, когда подсчитывается сумма квадратов отклонений от среднего арифметического
. С похожим ограничением мы сталкиваемся при расчете дисперсии или среднеквадратичного отклонения, когда подсчитывается сумма квадратов отклонений от среднего арифметического 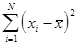 . Фиксированное значение
. Фиксированное значение 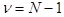 вместо
вместо 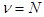 .
.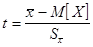 .
.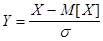 .
.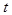 , подчиняющейся распределению Стьюдента, выражается формулой:
, подчиняющейся распределению Стьюдента, выражается формулой: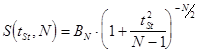 ,
, значительно отличается от нормальной кривой. По мере увеличения числа наблюдений N распределение Стьюдента довольно быстро приближается к нормальному распределению и уже при N= 20 практически не отличается от него. Оно отражает специфику изменения малой выборки (N <30), распределяющейся по нормальному закону в зависимости от N.
значительно отличается от нормальной кривой. По мере увеличения числа наблюдений N распределение Стьюдента довольно быстро приближается к нормальному распределению и уже при N= 20 практически не отличается от него. Оно отражает специфику изменения малой выборки (N <30), распределяющейся по нормальному закону в зависимости от N.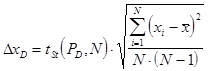 .
.
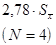
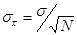 обозначена ошибка среднего для генеральной совокупности.
обозначена ошибка среднего для генеральной совокупности.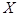 называют статистическим рядом. Например,
называют статистическим рядом. Например, 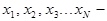 есть статистический ряд. Первый этап обработки этого экспериментального материала – составление вариационного ряда. Для этого из всей имеющейся выборочной совокупности находят наименьшее
есть статистический ряд. Первый этап обработки этого экспериментального материала – составление вариационного ряда. Для этого из всей имеющейся выборочной совокупности находят наименьшее 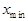 и наибольшее
и наибольшее 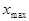 значения, фактически границы интервала, в котором лежат все вышеперечисленные значения
значения, фактически границы интервала, в котором лежат все вышеперечисленные значения 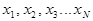 . Весь диапазон значений разбивается на классы (малые интервалы). Если совокупность имеет
. Весь диапазон значений разбивается на классы (малые интервалы). Если совокупность имеет 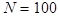 , то число классов можно взять равным
, то число классов можно взять равным 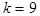 или
или 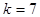 , где
, где 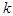 – число классов (малых интервалов).
– число классов (малых интервалов).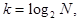 берется целая часть получившегося числа;
берется целая часть получившегося числа;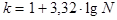 (формула Стерджеса, Sturges, 1926 г.);
(формула Стерджеса, Sturges, 1926 г.);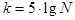 (формула К.Брукса и Н.Краузерса, 1963 г.).
(формула К.Брукса и Н.Краузерса, 1963 г.).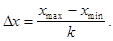
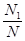
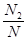
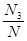
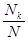
 - частота попадания в заданный интервал.
- частота попадания в заданный интервал.


