
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ошибка среднего арифметического или ошибка выборочности.Содержание книги
Поиск на нашем сайте
Пусть изучается некоторая достаточно большая совокупность. Методика измерений построена таким образом, что вся эта большая совокупность разделена на несколько малых выборок. Найдены средние арифметические значения исследуемого параметра для каждой выборки Распределение выборочных средних арифметических
где Тогда ошибка среднего арифметического:
Ошибку среднего арифметического часто называют ошибкой выборочности или ошибкой репрезентативности (representative). Чем больше объем выборки, тем меньше ошибка среднего арифметического, так как
то есть тем меньше расхождение между значениями признаков в выборочной совокупности и генеральной, характеристикой которого является истинное значение признака или математическое ожидание При увеличении объема
Распределение Стьюдента.
Нормальное распределение достаточно хорошо описывает поведение непрерывной случайной величины не только при Для таких ситуаций было предложено распределение случайной величины
Результат был указан в 1908 году английским исследователем Вильямом Госсетом, опубликовавшим свою работу под псевдонимом Стьюдент, но строго был получен З.Фишером в 1925 году. По виду эта формула напоминает выражение для нормированной случайной величины
Однако, между ними весьма существенная разница. В числителе вместо индивидуальных значений Х стоит выборочное среднее арифметическое, а в знаменателе вместо среднеквадратичного отклонения генеральной совокупности s стоит ошибка среднего арифметического для выборки. Плотность вероятности случайной величины
где BN зависит от объема выборки. При малых значениях N кривая плотности вероятности Практическим следствием открытия закона распределения Стьюдента явилось изменение формул, определяющих границы доверительного интервала для математического ожидания случайной величины при заданной доверительной вероятности РD. Доверительный интервал должен вычисляться по формуле:
Сравним значения доверительных интервалов в случае распределения Гаусса и распределения Стьюдента для одной и той же доверительной вероятности:
Через Исследования Стьюдента сыграли громадную роль, так как дали возможность работать с малыми выборками. Обратим еще раз ваше внимание на то, что главная задача, которую решает математическая статистика (ради чего, собственно говоря, эта наука и существует), заключается в том, чтобы на основании изучения выборки делать выводы о свойствах генеральной совокупности. Выборка - это лишь часть генеральной совокупности.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 и среднее арифметическое значение для всей большой совокупности (почти генеральной)
и среднее арифметическое значение для всей большой совокупности (почти генеральной)  . Если сравнить отклонения отдельных вариант
. Если сравнить отклонения отдельных вариант 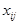 от общего среднего
от общего среднего  от общего среднего
от общего среднего  будет близко к нормальному, поэтому к нему относятся все закономерности нормального распределения. Тогда вариацию случайной величины
будет близко к нормальному, поэтому к нему относятся все закономерности нормального распределения. Тогда вариацию случайной величины  можно измерять своим среднеквадратичным отклонением
можно измерять своим среднеквадратичным отклонением  , которое называют ошибкой среднего арифметического. Исходя из того, что
, которое называют ошибкой среднего арифметического. Исходя из того, что  , можно утверждать, опираясь на строгое математическое доказательство, что
, можно утверждать, опираясь на строгое математическое доказательство, что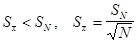 ,
, - по-прежнему объем выборки,
- по-прежнему объем выборки,  - оценка среднеквадратичного отклонения выборки.
- оценка среднеквадратичного отклонения выборки. .
. ,
,
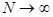 , но и при конечных, но достаточно больших объемах выборок (N >30). Что касается малых выборок (N <30), здесь распределение непрерывной случайной величины может заметно отличаться от нормального.
, но и при конечных, но достаточно больших объемах выборок (N >30). Что касается малых выборок (N <30), здесь распределение непрерывной случайной величины может заметно отличаться от нормального.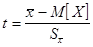 .
.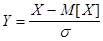 .
.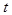 , подчиняющейся распределению Стьюдента, выражается формулой:
, подчиняющейся распределению Стьюдента, выражается формулой: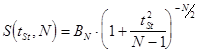 ,
, значительно отличается от нормальной кривой. По мере увеличения числа наблюдений N распределение Стьюдента довольно быстро приближается к нормальному распределению и уже при N= 20 практически не отличается от него. Оно отражает специфику изменения малой выборки (N <30), распределяющейся по нормальному закону в зависимости от N.
значительно отличается от нормальной кривой. По мере увеличения числа наблюдений N распределение Стьюдента довольно быстро приближается к нормальному распределению и уже при N= 20 практически не отличается от него. Оно отражает специфику изменения малой выборки (N <30), распределяющейся по нормальному закону в зависимости от N.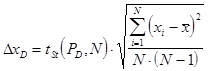 .
.
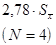
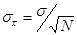 обозначена ошибка среднего для генеральной совокупности.
обозначена ошибка среднего для генеральной совокупности.


