
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полученную систему сил совместим с системой координат Х0Y.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(1) – сумма проекций всех сил на ось 0Х должна быть равна нулю (2) – сумма проекций всех сил на ось 0Х должна быть равна нулю. 7.1 Найдем углы между силами и осями координат (для этого введем дополнительные буквенные обозначения для удобства вычисления углов)
а) б) в) г) д) е) ж)
7.2 Рассмотрим уравнение (1) условия равновесия:
Вычислим проекцию каждой силы на ось 0Х.
а)
б)
в)
г)
Подставим значение проекций в уравнение (1)
7.3 Рассмотрим уравнение (2) условия равновесия:
Вычисляем проекцию каждой силы на ось 0Y:
а)
б)
в)
г)
Подставим значение проекций в уравнение (1)
Решим систему уравнений (1) и (2)
Получили систему двух линейных уравнений с двумя неизвестными (1)
(2)
Знак минус перед значением реакции
9. Проверка. Выполняется графическим способом: все силы ( 9.1 Вычислим масштаб для построения силового многоугольника с помощью выражения
(сила прямопропорциональна ее длине), где
Для вычисления масштаба длину первого вектора
Если то 9.2 Вычислим длины остальных векторов с помощью выражения
9.3 Построим правильную систему сил (с учетом направления вектора и рассчитанной длины): а) направление активных сил б) значение реакции связи в) значение реакции связи
Построим силовой многоугольник, для этого графически сложим все вектора данной системы. Вектора в силовом многоугольнике можно складывать в любой последовательности.
Ответ: Стержень АВ растягивается – реакция связи стержень ВС сжимается – реакция связи Пример 2 (задачи №11-№20). Определить реакции связей двухопорной балки.
Если q = 2 Оформление.
 Решение: Решение:
1. Введем следующее обозначение: Расстояния между опорами обозначим АВ.
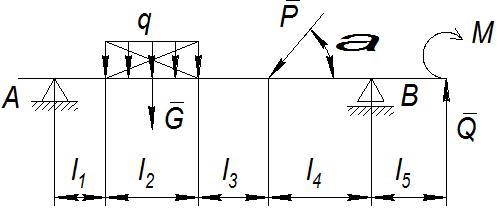
Рассмотрим равновесие балки АВ. Определим активные силы (нагрузки), действующие на балку АВ.
а) равномерно-распределенная нагрузка, которая задана интенсивностью q и длиной действия l; Ее действие заменяем равнодействующей силой G, которая приложена посередине нагруженного участка и равна:
В данном случае q = 2
б) сосредоточенная сила P, которая действует под углом 20º к оси балки; в) сосредоточенная сила г) пара сил с моментом М.
4. Определим виды связей, участвующих в задаче: а) связь в точке А: шарнирно-неподвижная опора, величина и направление реакции которой неизвестны; б) связь в точке В: шарнирно-подвижная, ее реакция направлена перпендикулярно к плоскости катания. 5. при действии активных сил (нагрузок) на балку в связях возникают реакции связей 6. Для удобства решения связи отбрасываем и заменяем их реакциями связей: а) в точке А направление реакции б) в точке В реакция
Итак, на балку АВ действуют: а) активные силы: равномерно-распределенная нагрузка б) реактивные силы (реакции связей): реакция связи Это является системой сил для данной балки.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.121.42 (0.008 с.) |


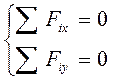 7. Составим условие равновесия и вычислим реакции стержней
7. Составим условие равновесия и вычислим реакции стержней  и
и  .
.
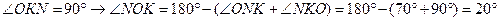
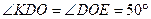 (внутренние накрест лежащие углы)
(внутренние накрест лежащие углы)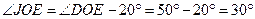
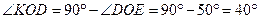
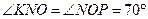

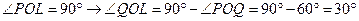




 - действует под углом 30° к оси 0Х:
- действует под углом 30° к оси 0Х: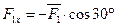
 - действует под углом 60° к оси 0Х:
- действует под углом 60° к оси 0Х:
 - действует под углом 20° к оси 0Х:
- действует под углом 20° к оси 0Х:
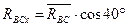


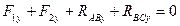

 (или
(или 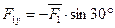 )
) (или
(или  )
) (или
(или 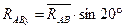 )
) (или
(или 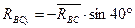 )
)
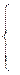

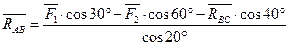
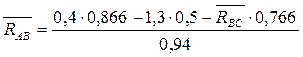
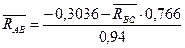






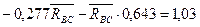
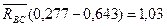


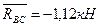
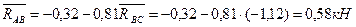
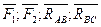 ) пересекаются в точке В и находятся в равновесии, значит силовой многоугольник, построенный на этих силах должен быть замкнутым.
) пересекаются в точке В и находятся в равновесии, значит силовой многоугольник, построенный на этих силах должен быть замкнутым.
 -сила;
-сила; - коэффициент пропорциональности (масштаб);
- коэффициент пропорциональности (масштаб);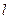 - длина вектора;
- длина вектора;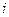 - порядковый номер вектора.
- порядковый номер вектора.
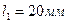 ,
, .
.
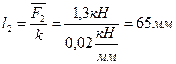
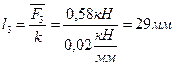
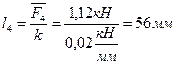


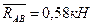 ;
;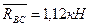 .
.
 ;
;  = 10
= 10 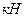 ; М = 8
; М = 8  ;
;  = 15
= 15 

 -?
-?
 -?
-?
 .
.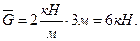
 и
и  ;
;
 , сосредоточенные силы
, сосредоточенные силы 


