
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6: Использование элементарных функций (часть 1)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Функции – это специальные, заранее созданные формулы, которые позволяют легко и быстро выполнять сложные вычисления. Функции позволяют: § Упрощать формулы; § Осуществлять с помощью формул такие вычисления, которые невозможно выполнить по-другому; § Ускорять выполнение некоторых задач редактирования; § Выполнять «условное» вычисление по формулам, позволяющее реализовать простые алгоритмы принятия решений. В поставку Excel входит более 300 функций, которые выполняют широкий спектр различных вычислений. Некоторые функции, такие как СУММ, SIN и ФАКТР, являются эквивалентными длинных математических формул, которые вы можете создать сами. Другие функции, такие как ЕСЛИ и ВПР, в виде формул реализовать невозможно. Если ни одна из встроенных функций не подходит для решения вашей задачи, можно создать пользовательские функции. Excel делит все функции на следующие категории: § Финансовые – функции для расчёта амортизации имущества, стоимости основных фондов, нормы прибыли, величины выплат на основной капитал и других финансовых показателей; § Дата и время – операции прямого и обратного преобразования даты и времени в текстовые строки; § Математические – математические и тригонометрические функции, некоторые из них приведены в таблице 1; § Статистические – функции для расчёта среднего значения, дисперсии, статистических распределений и других вероятностных характеристик; § Ссылки и массивы – операции преобразования ссылки на ячейку в число, расчёта ссылок на основе числовых аргументов, вычисления числа строк и столбцов диапазона и других параметров, связанных с адресацией ячеек листа Excel; § Работа с базой данных - функции формирования выборки из базы данных и расчёта статистических параметров величин, расположенных в базе данных; § Текстовые – функции для работы с текстовыми строками;
Пример функции Ниже приведён пример того, как встроенные функции позволяют упростить формулу. Среднее значение чисел, находящихся в десяти ячейках А1:А10, можно вычислить по следующей формуле: = (А1 + А2 + А3 + А4 + А5 + А6 + А7 + А8 + А9 + А10) / 10 Согласитесь, что это не самая удобная формула. Если в данную формулу потребуется добавить новые ячейки, сделать это будет нелегко. Но вы можете заменить эту формулу очень простой в употреблении встроенной Excel: = СРЗНАЧ (А1:А10) Аргументы функций Вы, вероятно, заметили в предыдущем примере, что в функции используются круглые скобки. Они есть у всех функций. Данные внутри круглых скобок называются аргументами. Функции различаются по тому, как они используют аргументы. В зависимости от этого, определяются следующие типы функций: § Функции без аргументов; § Функции с одним аргументом; § Функции с фиксированным числом аргументов; § Функции с неопределённым числом аргументов; § Функции с необязательными аргументами. Примером функции, не использующей аргумент, может служить функция СЛЧИС, которая генерирует случайное число в интервале между 0 и 1. Даже если функция не использует аргумент, вы всё равно должны набрать пустые круглые скобки следующем образом: =СЛЧИС () Если в функции используется несколько аргументов, то каждый из них отделяется точкой с запятой. В примере, приведенном в начале, в качестве аргументов использовались адреса ячеек. Однако Excel — очень гибкая система в плане использования аргументов функции. В формуле достаточно указать только адрес ячейки (независимо от того, что конкретно находится в самой ячейке: литерал, текстовая строка или выражение).
Использование имен в качестве аргументов Как вы ужезнаете, в качестве аргументов функции могут использоваться ссылки на ячейку или диапазон. При вычислениях Excel использует текущее содержимое ячейки или диапазона. Например, функция СУММ вычисляет сумму своих аргументов. Для вычисления суммы величин,находящихся в диапазоне ячеек Al:D20, можно использовать следующую формулу: = CУMM (A1:D20) Однако если вы определите имя для диапазона Al:D20, например Продажи, его можно использовать вместо ссылки: = СУММ (Продажи) В некоторых случаях нужно использовать в качестве аргумента функции весь столбец или строку. Например, следующая формула суммирует все значения, находящиеся в столбце В: =СУММ (В: В) Этот метод особенно эффективен, если диапазон суммирования изменяется (например, если вы постоянно добавляете новые суммы продаж).
Аргументы – литералы Литералом называют число или строку текста, которые непосредственно заданы в качестве аргументов функции. Например, функция КОРЕНЬ содержит один аргумент-литерал. Ниже приведен пример формулы, в которой в качестве аргумента использован литерал: = КОРЕНЬ (225) Использование аргументов-литералов в простых функциях, подобных приведенной выше, лишено всякого смысла, ведь эта формула всегда возвращает одно и то же значение 15, которое можно ввести вручную. Использование литералов имеет смысл только в формулах, в которых употребляется несколько аргументов. Для примера возьмем функцию ЛЕВСИМВ, которая имеет два аргумента. Она возвращает строку символов, начиная с первого аргумента, длина которой определяется вторым аргументом. Так, если в ячейке A1 находится текст Бюджет, то следующая формула выделит первую букву этого слова, т.е. Б: = ЛЕВСИМВ (А1;1) Аргументы – выражения В Excel в качестве аргументов функции можно также использовать выражения. Выражения можно считать формулой внутри формулы. Когда Excel сталкивается с выражением в качестве аргумента функции, программа вначале вычисляет его, а затем использует полученный результат в качестве значения аргумента функции, например: = КОРЕНЬ ((А1 ^ 2) + (А2 ^ 2)) В этой формуле используется функция КОРЕНЬ, единственным аргументом которой является выражение (A1 ^ 2) + (А2 ^ 2). Когда программа приступает к вычислению такой функции, вначале определяется значение аргумента, а затем из него извлекается квадратный корень.
Функции в качестве аргументов Поскольку в качестве аргументов функций в Excel могут использоваться выражения, нет ничего удивительного в том, что в эти выражения могут включаться другие функции. Функции, которые используются в формуле в качестве аргументов других функций, называют вложенными. Сначала Excel вычислит значение самого глубоко вложенного выражения. Вот пример вложенной функции: = SIN (РАДИАНЫ (В9)) Функция РАДИАНЫ преобразует значение аргумента, заданное в градусах, в радианы, поскольку во всех тригонометрических функциях Excel аргументы задаются именно в радианах. Поэтому, если в ячейке В9 значение величины угла измеряется в градусах, сначала функция РАДИАНЫ преобразует его в радианы, а затем функция SIN вычисляет синус угла. Вложенность функций ограничивается только общей длиной строки формулы — 1024 символа. Способы ввода функций Есть два пути ввода функции в формулу: вручную или с использованием средства Мастер функций.
Ввод функций вручную Если вы уже знакомы с функциями, то наверняка знаете о том, какое количество аргументов разнообразных типов они используют. Один из методов ввода функций заключается в том, что нужно ввести с помощью клавиатуры имя функции и список ее аргументов. Очень часто этот метод оказывается самым эффективным. Если вы забыли закрыть скобки, Excel сделает это автоматически. Например, если вы ввели = СУММ (А1: С12 и нажали клавишу <Enter>, то Excel исправит формулу, добавив правую скобку.
Вставка функции в формулу Для того чтобы вставить функцию, сначала выделите ее в диалоговом окне Мастер функций – шаг 1 из 2 (Рис. 5.2). Открыть это окно можно одним из следующих способов. § Перейдите на вкладку «Формулы». § Щелкните на кнопке «Вставить функцию» (рис.5.1), которая находится на стандартной панели инструментов.
Диалоговое окно Мастер функций помогает выбрать нужную функцию, даже если вы не знаете точно, какую функцию следует применить. В этом окне сначала выберите категорию (или Полный алфавитный перечень) в списке Категория и затем в алфавитном списке Функция укажите нужную функцию. В качестве альтернативы после выбора категории можно щелкнуть на имени любой функции в списке Функция и нажать клавишу, соответствующую первой букве нужного имени. Чтобы ввести функцию, нажмите кнопку ОК или клавишу Enter. Excel введет знак равенства (если вы вставляете функцию в начале формулы), имя функции и пару круглых скобок. Затем Excel откроет второе окно диалога мастера функций (без строки заголовка), показанное на Рис.5.3.
Второе окно диалога мастера функций содержит по одному полю для каждого аргумента выбранной функции. Если функция имеет переменное число аргументов, это окно диалога при вводе дополнительных аргументов расширяется. Описание аргумента, поле которого содержит точку вставки (курсор), выводится в нижней части окна диалога. Справа от каждого поля аргумента отображается его текущее значение. Это очень удобно, когда вы используете ссылки или имена. Текущее значение функции отображается внизу окна диалога. Нажмите кнопку ОК или клавишу Enter, и созданная функция появится в строке формул.
Математические функции В Excel включено около 50 функций этой категории, чего вполне достаточно для выполнения сложных математических расчётов. В этой категории представлены как обычные функции типа СУММ или ЦЕЛОЕ, так и множество «экзотических» функций, одна из которых может оказаться именно той, которую вы так давно искали. Основные функции представлены в таблице 5.1.
Таблица 5.1
Функция ЦЕЛОЕ Эта функция возвращает целую часть числа, отбрасывая все дробные цифры после десятичной, запятой. Ниже приведен пример использования этой функции, которая возвращает результат 412:
= ЦЕЛОЕ (412, 98)
Функция ОКРУГЛ Эта функция округляет значение числа до указанного количества десятичных разрядов. Функция ОКРУГЛ обычно используется для контроля точности вычислений. Она имеет два аргумента: первый — значениедля округления, второй — количество цифр после запятой. Если второй аргумент отрицательный, округление смещается влево от запятой на заданноеколичество цифр. В табл. 5.2 приведены некоторые примеры использования этой функции. Таблица 5.2
Если при вычислениях вам нужно что-то округлить, попробуйте воспользоваться функциями ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ. Кроме того, существуют функции ОКРВНИЗ и ОКРВВЕРХ, которые позволяют округлить значение до указанного кратного. Например, вы можете использовать функцию ОКРВНИЗ для округления значения до ближайшего числа, кратного десяти (128,5 будет округлено до 120).
Функция ПИ Эта функция возвращает значение числа π с 14 знаками после запятой. Функция ПИ не требует аргумента и является сокращенным обозначением числа 3,14159265358979. В следующем примере подсчитывается площадь круга, радиус которого хранится в ячейке под именем Радиус:
= ПИ () * (Радиус ^ 2)
Функция SIN Эта функция возвращает синус угла, определяемый как отношение противолежащего катета к гипотенузе прямоугольного треугольника. Функция SIN имеет один аргумент — значение угла, выраженное в радианах. Для перевода градусов в радианы используйте функцию РАДИАНЫ. Существует также функция ГРАДУСЫ, выполняющая обратную операцию. Например, если в ячейке F21 находится значение угла, выраженное в градусах, то формула для вычисления синуса будет иметь следующий вид:
= SIN (РАДИАНЫ(F 21))
В Excel включен полный набор тригонометрических функций. Чтобы получить более подробную информацию о них, прочитайте соответствующие разделы справки Excel.
Функция КОРЕНЬ Эта функция возвращает значение квадратного корня из аргумента. Если аргумент отрицательный, функция воспринимает его как ошибку. В результате выполнения следующего примера будет возвращено число 32:
= КОРЕНЬ (1024)
Для вычисления других корней используйте функцию СТЕПЕНЬ. Например, для получения кубического корня из числа 327 можно применить формул:
= СТЕПЕНЬ(327;1/3)
Округление с помощью функций ЧЁТН и НЕЧЁТ Для выполнения операций округления можно использовать функции ЧЕТН и НЕЧЕТ. Функция ЧЕТН округляет число вверх до ближайшего четного целого числа. Функция НЕЧЕТ округляет число вверх до ближайшего нечетного целого числа. Отрицательные числа округляются не вверх, а вниз. Эти функции имеют следующий синтаксис: = ЧЕТН (число) = HEЧЕT (число)
Функции ЦЕЛОЕ и ОТБР
Функция ЦЕЛОЕ округляет число вниз до ближайшего целого и имеет следующий синтаксис:
= ЦЕЛОЕ (число) Аргумент число — это число, для которого вы хотите найти следующее наименьшее целое. Например, рассмотрим формулу:
= ЦЕЛОЕ (100, 01)
Эта формула возвратит значение 100, как и следующая формула, несмотря на то, что число 100,99999999 уже практически равно 101:
= ЦЕЛОЕ (100, 99999999)
Если число отрицательное, функция ЦЕЛОЕ также округляет это число вниз до ближайшего целого. Например, следующая формула возвращает значение — 101:
= ЦЕЛОЕ (-100,99999999)
Функция ОТБР отбрасывает все цифры справа от десятичной запятой независимо от знака числа. Необязательный аргумент количество_цифр задает позицию, после которой производится усечение (описание этого аргумента см. в функции ОКРУГЛ). Эта функция имеет следующий синтаксис:
= ОТБР (число; количество цифр)
Если второй аргумент опущен, он принимается равным нулю. Например, следующая формула возвращает значение 13: = OTБP (13, 978)
Функция ОСТАТ Функция ОСТАТ возвращает остаток от деления и имеет следующий синтаксис:
= ОСТАТ (число; делитель)
Значение функции ОСТАТ — это остаток, получаемый при делении аргумента число на делитель. Например, следующая функция возвратит значение 1, то есть остаток, получаемый при делении 9 на 4:
= OCTAT (9; 4)
Если число меньше, чем делитель, то значение функции равное аргументу число. Например, следующая функция возвратит значение 5:
= ОСТАТ (5;11)
Если число точно делится на делитель, функция возвращает 0. Если делитель равен 0, функция ОСТАТ возвращает ошибочное значение #ДЕЛ/0! (#DIV/0!). Функция СУММ Если взять наугад несколько рабочих книг, то можно смело поспорить, что чаще всего в них будет использоваться функция СУММ. Эта функция — одна из самых простых. Она может иметь от 1 до 30 аргументов. Для того чтобы подсчитать сумму значений ячеек трех диапазонов (А1:А10, С1:С10 и Е1:Е10), можно использовать три аргумента:
= СУММ (А1:А10;С1:С10;Е1:Е10)
Аргументы не обязательно должны быть заданы только в таком виде. Например, вы можете использовать адреса отдельных ячеек, ссылки на диапазоны и литералы следующим образом:
= СУММ (А1;С1:С10;125)
В связи с такой популярностью функции СУММ разработчики Excel очень упростили ее использование и практически автоматизировали его. Чтобы вставить формулу, в которой используется функция СУММ, щелкните на кнопке Автосумма, находящейся на стандартной панели инструментов.
Функция СУММЕСЛИ Эта функция полезна при подсчете условных сумм. Функция СУММЕСЛИ имеет три аргумента. Первый — это диапазон ячеек, содержимое которых должно быть отобрано по определенному критерию. Второй аргумент — критерий отбора, в примере это название региона. Третий аргумент — диапазон ячеек, значение которых нужно просуммировать в случае, если выполняется данный критерий.
Упражнения ПРИМЕР 1
Вычислить log 32 + 1.
Решение 1. Присвоим ячейкам А1 и В1 имена x и y. Поместим в А1 число 4, а в В1 число 3. 2. Выделим ячейку А4. 3. Вызываем Мастера функций. 4. Получаем окно первого шага Мастера функций: «Мастер функций – шаг 1 из 2». 5. Логарифм относится к математическим функциям, поэтому выбираем в списке Категория «Математические» (если Вы не можете отнести функцию к какой–либо категории, то обратитесь к пункту «Полный алфавитный перечень»). 6. Теперь в правом окне, в списке Функция, выбираем LOG. В нижней части окна появляется краткое описание функции: LOG(число;основание_логарифма) Возвращает логарифм числа по заданному основанию Из описания ясно, что эта функция нам подходит.
7. Щёлкаем ОК и переходим к следующему диалоговому окну. В этом окне поля ввода аргументов функции: Число и Основание_логарифма. 8. В первом поле вводим число 2. 9. Если мы не укажем во втором поле (необязательный) аргумент, то будет подразумеваться основание 10. Обратите внимание: ниже и правее полей ввода появился результат 0.301029996 – это lg 2, т.е. десятичный логарифм двух. Вводим число 3. Ниже и правее полей ввода появляется результат 0.630929754. 10. Если мы сейчас нажмём ОК, то ввод формулы завершится и придётся её корректировать, чтобы добавить слагаемое +1. Поэтому поступим так: находясь во втором окне Мастера функций, щёлкаем мышью в поле ввода сразу вслед за сформированной частью формулы =LOG(2,3) и введём недостающее слагаемое +1. 11. Окончательный вид формулы =LOG(2,3)+1. Нажмём клавишу Enter. 12. Результат: 1.63093.
ПРИМЕР 2
ВЛОЖЕННЫЕ ФУНКЦИИ
Введём в ячейку A5 формулу для вычисления функции. Эта функция представляет собой композицию двух функций: w =
Решение Выделяем ячейку А5. Щёлкаем кнопку со значением равенства слева от строки ввода. Выбираем КОРЕНЬ. Находясь в поле ввода аргумента функции КОРЕНЬ, в панели функций выбираем TAN и в поле ввода аргумента этой функции вводим имя х. А теперь внимание! Мы не щелкаем кнопку ОК, как следовало бы ожидать, — это досрочно завершит ввод формулы (испытайте это). Вместо этого устанавливаем в поле ввода курсор на функции КОРЕНЬ (т.е. на внешней функции). Тот- час второе окно Мастера функций для TAN заменяется на второе окно Мастера функций для функции КОРЕНЬ. В поле ввода аргумента отображается TAN(x). Добавляем к этой функции +1 и щелкаем ОК. Результат: 1.468952. Обратите внимание, когда Вы находились во втором окне Мастера функций для функции TAN() и ввели в качестве аргумента X, то справа от поля ввода аргумента Вы видите =4, ниже Вы видите =1.157821282 (это значение tg 4), а в самом низу окна Вы видите: Значение: 1.076021042. Это вычисленное значение формулы =KOPEHЬ(TAN(x)), которая присутствует сейчас в строке ввода. Еще заметим, что в диалоговом окне второго шага Мастера функций справа от каждого поля ввода для аргументов функции имеется кнопка свертывания/развертывания. Ее назначение нам уже известно. Если нужно ввести адрес ячейки или блока, то следует щелкнуть по этой кнопке, тогда диалоговое окно свернется в поле ввода и можно без помех сделать нужное выделение на рабочем листе. В прежних версиях Excel приходилось таскать мышью по экрану диалоговое окно, ухватив его за заголовок.
Практические задания: 1. Присвойте ячейкам А1 и В1 имена X и Y соответственно. 2. Поместите в эти ячейки числа, указанные в вашем варианте (см. таблицу). 3. В А4 вычислите sin(0,8721356864) 4. В В4 вычислите 5. В ячейке А5 вычислите: 6. Скопируйте полученное значение в ячейку А6 и округлите результат вычисления до сотых (используя необходимую функцию). 7. В ячейке С5 вычислите: 8. В С6 округлите результат вычисления до ближайшего чётного целого (используя необходимую функцию). 9. В ячейке Е5 вычислите:
10. В Е6 округлите результат вычисления до ближайшего нечётного целого (используя необходимую функцию).
11. В ячейке D4 вычислите:
12. В ячейках A8 и В8 вычислите значения 13. В ячейку С1 запишите любую десятичную дробь. Получите в ячейке D1 первую цифру из дробной части числа (используя необходимую функцию).
14. В B5 вычислите: сумму всех полученных результатов вычислений.
ЛАБОРАТОРНАЯ РАБОТА № 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.014 с.) |

 Рис. 5.1
Рис. 5.1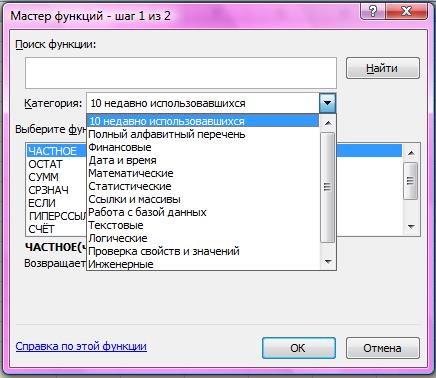 Рис. 5.2
Рис. 5.2 Рис. 5.3
Рис. 5.3 и z = tgx + 1. Соответствующие функции Excel: КОРЕНЬ(z) и TAN(х) + 1.
и z = tgx + 1. Соответствующие функции Excel: КОРЕНЬ(z) и TAN(х) + 1.
 .
. .
.

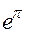 и
и  , соответственно (используя функции EXP() и ПИ(), которые не имеют аргументов).
, соответственно (используя функции EXP() и ПИ(), которые не имеют аргументов).


