
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы выявления тенденций в развитии явлений (метод укрупнения интервалов, метод скользящей средней).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития. При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы. Одним из приемов выявления основной тенденции является метод укрупнения интервалов. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т. д. Другой прием — метод скользящей средней. Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени: где
Выявление основной тенденции развития с помощью аналитического выравнивания динамического ряда. Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени: Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции производится на основе анализа характера закономерностей динамики данного явления. Для выравнивания ряда динамики по прямой используется уравнение:
Изучение сезонных колебаний в рядах динамики. При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или за несколько лет. При изучении сезонных колебаний используются специальные показатели — индексы сезонности (Is). Способы определения индексов сезонности различны; они зависят от характера основной сезонности ряда динамики.
Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна (или она не наблюдается совсем), изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Определение индексов сезонности в таких рядах производится по формуле: Прогнозирование рядов динамики(РД) и определение доверительных интервалов прогноза. Экстраполяция -метод прогнозирования, при кот. обнаруженная тенденция переносится в будущее. При этом предполаг-ся, что размер признака, хар-щего явл-ие формир-ся под воздействием мн-ва факторов, причём не представляется возможным выделить порознь их влияний.В связи с этим ход разв-я связыв-ся не с конкретным фактором, а с течением времени. Экстраполяция возможна если выполн-ся 2 усл-я: 1) разв-е явл-я с достаточным основанием м б охар-но плавной траектории, т.е трендом; 2 ) общие усл-я, определ-щие разв-е явл-я в прошлом, не претерпят существенных измен-й в будущем. Механически экстраполяция осущ-ся подстановкой соот-щего зн-я t в урав-е, опис-щее тренд. Т обр, получают точечную оценку прогноза Поскольку экон. переменные,как правило, непрерывны, то указание только их точечных знач-й лишено содержания. Исходя из этого определяют доверит-ные интервалы прогноза
SE-cр квадр ошибка модели te-номер прогнозир-го периода
n-число наблюдений
m-число параметров
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.138.113 (0.011 с.) |

 При этом каждый фактический уровень yi рассматривается как сумма двух составляющих:
При этом каждый фактический уровень yi рассматривается как сумма двух составляющих: 
 — систематическая составляющая, отражающая тренд и выраженная определенным уравнением, а
— систематическая составляющая, отражающая тренд и выраженная определенным уравнением, а  — случайная величина, вызывающая колебания уровней вокруг тренда.
— случайная величина, вызывающая колебания уровней вокруг тренда. При этом каждый фактический уровень yi рассматривается как сумма двух составляющих:
При этом каждый фактический уровень yi рассматривается как сумма двух составляющих:  — систематическая составляющая, отражающая тренд и выраженная определенным уравнением, а
— систематическая составляющая, отражающая тренд и выраженная определенным уравнением, а 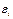 — случайная величина, вызывающая колебания уровней вокруг тренда.
— случайная величина, вызывающая колебания уровней вокруг тренда.
 где
где  — осредненные эмпирические уровни ряда по одноименным периодам;
— осредненные эмпирические уровни ряда по одноименным периодам;  — общий средний уровень ряда. В ряду динамики с ярко выраженной тенденцией развития формула расчета индекса сезонности имеет следующий вид:
— общий средний уровень ряда. В ряду динамики с ярко выраженной тенденцией развития формула расчета индекса сезонности имеет следующий вид:  где
где  — исходные (эмпирические) уровни ряда;
— исходные (эмпирические) уровни ряда;  — выровненные (теоретические) уровни ряда; n — число годовых периодов.
— выровненные (теоретические) уровни ряда; n — число годовых периодов. , где l-период упреждения числа, на кот осущ-ся прогноз; Sp – ср.квадратич. ошибка прогноза;
, где l-период упреждения числа, на кот осущ-ся прогноз; Sp – ср.квадратич. ошибка прогноза;
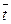 -номер периода, стоящего в середине ряда
-номер периода, стоящего в середине ряда



