
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы отбора единиц в выборочную совокупность.Содержание книги
Поиск на нашем сайте Для того чтобы по выборке можно было сделать вывод о св-вах генеральной сов-сти, выборка д б репрезентативной. Т.е. она должна наиболее полно и адекватно представлять св-ва генер сов-сти. Репрезентативность выборки м б обеспечена только при объективности отбора данных. Возможны 3 способа отбора: 1)Случайный отбор; 2)Отбор по определенной схеме; 3)Сочетание первого и второго способов. Если отбор в соотв-вии с принятой схемой произв-ся из генер сов-сти, предварительно разделенной на типы, то выборка наз-ся типической или стратифицированной. Другое деление выборки по видам опред-ся тем, что явл-ся единицей отбора: либо это единица наблюдения, либо серия единиц (серийная выборка). В мат ст-ке обяз-но вводят деление выборки на повторную и бесповторную. Первая осущ-ся по схеме возвратного шара; вторая – безвозвратного шара (шар вынимается из корзины и обратно туда не возвращ-ся). В соц-экон ст-ке нет смысла применять повторную выборку, поэтому как правило имеется в виду бесповторный отбор. Поскольку соц-эк объекты имеют сложную стр-ру, то выборку бывает довольно трудно орг-ть, поэтому применяют многоступенчатую выборку, в которой на каждой ступени исп-ся разные единицы отбора: более крупные – на нач ступенях, на последней ступени – единица отбора совпадает с единицей наблюдения. Исп-ся многофазовая выборка, включающая определенное кол-во фаз, каждая из кот отличается подробностью программы наблюдения.
Ошибки выборочного наблюдения. Ошибка выборки или ошибка репрезентативности – это разница между знач-ем пок-ля, получ-го на выборке, и генеральным параметромом. Расчет ошибок позволяет решить одну из главных проблем орг-ции выборочного наблюдения — оценить репрезентативность (представительность) выборочной сов-сти. Различают среднюю и предельную ошибки выборки. Эти 2 вида связаны след соотношением:
Где Δ-предельная ошибка выборки;t-коэф-т доверия. Определяемый в завсим-ти от ур-ня вероятности;Sx-средняя ошибка выборки Величина средней ошибки выборки рассчитывается дифференцированно в завис-ти от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка опред-ся по формуле:
При бесповторном: где σ2— выборочная (или генеральная) дисперсия; σ— выборочное (или генеральное) среднее квадратическое отклонение; n- объем выборочной совокупности; N — объем генеральной сов-сти. Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в кот будут нах-ся хар-ки генер сов-ти.Н-р, для выьор средней такие пределы устан-ся на основе след соотношений:
Где μ и х¯-генер и выборочная средние соответственно,Δх — предельная ошибка выборочной средней. Для типической выборки средняя ошибка вычисл-ся по формулам: -при отборе, пропорциональном объёму типических групп
-при отборе, пропорциональном вариации признака(не пропорцион-ных объёму групп)
При серийной выборке ср ошибка опр-ся след обр:
Где R-число серий в генер сов-ти;r-число серий в выборочной сов-ти; σ2- межгруп дисперсия
Определение необходимой численности выборочного наблюдения. Прежде чем приступить к проведению выборочного наблюдения, надо установить необходимую численность выборки, т.е. объем выборки, необходимый для того, чтобы обеспечить результаты выборочного наблюдения с заранее установленной точностью. Необходимая численность выборки (n) определяется на основе формул предельной выборки. Так, если выборка повторная, то n определяется из формулы
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |





 (повторный отбор)
(повторный отбор) (бесповторный отбор)
(бесповторный отбор)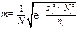 (повторный отбор)
(повторный отбор) (бесповт отбор)
(бесповт отбор) (повт отбор)
(повт отбор) (бесповт отбор)
(бесповт отбор) , где t-коэфф. доверия. Чтобы найти необход. числ-ть выборки (n), нужно выразить ее из предыд-ей фор-лы, т.е. n = =(t2*б2)/r2. Для бесповторного отбора численность выборки опред-ся из фор-лы:
, где t-коэфф. доверия. Чтобы найти необход. числ-ть выборки (n), нужно выразить ее из предыд-ей фор-лы, т.е. n = =(t2*б2)/r2. Для бесповторного отбора численность выборки опред-ся из фор-лы:  . Необходимая численность выборки находится путем выражения n из пред-щей фор-лы: n = (t2 * б2 * N) / (r2* N + t2 * б2), где n – объем выборки, N – объем генер. сов-ти.
. Необходимая численность выборки находится путем выражения n из пред-щей фор-лы: n = (t2 * б2 * N) / (r2* N + t2 * б2), где n – объем выборки, N – объем генер. сов-ти.


