Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регулирование частоты вращения двигателя постоянного токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ДПТ имеют две обмотки: обмотку возбуждения и обмотку управления. При этом напряжение управления может подаваться либо на обмотку якоря, либо на обмотку возбуждения. Поэтому различают якорное и полюсное управление.
Напряжение возбуждения подается на обмотку полюсов, напряжение управления - на обмотку якоря. Коэффициент сигнала a здесь равен a = Uу/Uв. Для двигателей с постоянными магнитами a = Uу/Uу.ном. Регулирование частоты вращения осуществляется изменением напряжения управления. При отсутствии насыщения Фв= kфUв, а поскольку Uв = const, магнитный поток возбуждения также остается постоянным, т.е. Фв = const. Ток якоря:
где Е = сеФвn = сеkфUвn – ЭДС якоря; rа- сопротивление якорной цепи. Вращающий момент двигателя
Выразим момент в относительных единицах, приняв за базовый момент пусковой момент, развиваемый двигателем при n = 0 и a = 1
Тогда относительное значение момента m = M/Mб
Частота вращения при холостом ходе (m = 0 и a = 1)
Откуда находим cеkф= 1/nо. Подставляя это значение в (1.1), получим
где n = n/nо- относительная частота вращения двигателя.
Уравнение (1.3) есть уравнение механической характеристики исполнительного двигателя при якорном управлении. Решив его относительно n, получим уравнение регулировочной характеристики Механическая мощность в относительных единицах рмх = mn = n(a - n). Угловую скорость, при которой наступает максимум мощности, найдем известным приемом (dpмх/dn = 0), откуда nм= a/2, а максимальное значение механической мощности будет
Мощность управления Приняв за базовую единицу мощность управления при коротком замыкании Ру.к (n = О, a = 1)
получим мощность управления в относительных единицах Мощность возбуждения
На рис. 1.2,а представлены механические, на рис. 1.2,б - регулировочные характеристики, а на рис. 1.3 показана зависимость рмх = f(n) исполнительного двигателя. Проанализируем свойства двигателя при якорном способе управления. Механические характеристики линейные и параллельные, что означает независимость быстродействия от коэффициента сигнала. Пусковой момент и угловая скорость холостого хода пропорциональны коэффициенту сигнала.
Рис.1.2. Механические (а) и регулировочные (б) характеристики исполнительного двигателя постоянного тока при якорном управлении
Рис. 1.3. Зависимость механической мощности от скорости вращения при якорном управлении
Мощность управления резко возрастает с увеличением коэффициента сигнала. Кроме того, она доходит до 95 % полной потребляемой мощности двигателя, поскольку является мощностью якорной цепи, что характерно для двигателей постоянного тока. В данном случае это является существенным недостатком якорного управления, ибо предполагает наличие мощных и дорогих усилителей. Мощность возбуждения остается величиной постоянной, независящей ни от коэффициента сигнала, ни от частоты вращения. К тому же - она небольшая по величине, что также характерно для машин постоянного тока. Максимум механической мощности в сильной степени зависит от коэффициента сигнала и даже при a = 1 не превышает 1/4 базовой мощности. 2. Полюсное управление исполнительным двигателем
Рис. 1.4. Схема включения исполнительного двигателя при полюсном управлении
Если пренебречь насыщением магнитной цепь, можно считать Ф = kфUу = kфaUв. Тогда ток якоря
Вращающий момент
Принимая за базовый момент пусковой (n = 0, a =1))
получим относительное значение момента
Решив его относительно n, получим уравнение регулировочной характеристики
Механическая мощность в относительных единицах рмх= mn = an - a2n2. Скорость, при которой наступает максимум мощности nм = 0,5/a. Тогда максимальная механическая мощность будет
Мощность управления
На рис. 1.5,а представлены механические, на рис. 1.5,б - регулировочные характеристики, двигателя при полюсном управлении.
Рис.2.5. Механические (а) и регулировочные (б) характеристики двигателя постоянного тока при полюсном управлении Проанализируем эти графики. Механические характеристики линейные, но непараллельные, к тому же и неоднозначные (одну и ту же частоту вращения можно получить при разных значениях a). Пусковой момент прямо-, а частота вращения холостого хода обратно пропорциональны коэффициенту сигнала и при малых a может существенно превышать номинальную, что безусловно опасно для двигателя. Регулировочные характеристики нелинейные, а при m < 0,5 неоднозначные. По этой причине полюсное управление используют лишь при m > 0,5. Мощность управления пропорциональна квадрату коэффициента сигнала и не зависит от частоты вращения. Она значительно меньше, чем при якорном управлении, что является достоинством данного способа. Мощность возбуждения с увеличением частоты вращения уменьшается и тем быстрее, чем больше a. Максимум механической мощности не зависит от коэффициента сигнала, что также можно отнести к достоинствам полюсного управления. Несмотря на отмеченные достоинства полюсного управления, предпочтение все-таки следует отдать якорному потому, что оно обеспечивает линейные и однозначные характеристики, в принципе исключает самоход (при полюсном он возможен из-за взаимодействия тока якоря с потоком остаточной намагниченности полюсов), обладает более высоким быстродействием, поскольку индуктивность якоря меньше индуктивности обмотки возбуждения.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.116.245 (0.01 с.) |

 1 Якорное управление двигателем
1 Якорное управление двигателем
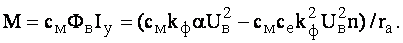

 (1.1)
(1.1) (1.2)
(1.2)
 (1.4)
(1.4)
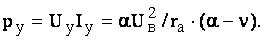

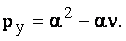
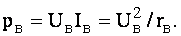





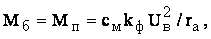

 С учетом (1.2) уравнение механической характеристики примет вид
С учетом (1.2) уравнение механической характеристики примет вид