
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели сезонности: аддитивная и мультипликативнаяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Учет сезонности при построении модели регрессии
· z1 = 1 – для первого квартала, · 0 – для остальных; · z2 = 1 – для второго квартала, · 0 – для остальных; · z3 = 1 – для третьего квартала, · 0 – для остальных. Аддитивная модель yt = T+S+E модель, в которую факторы входят в виде алгебраической суммы Мультипликативная модель yt = T*S*E модель, в которую факторы входят в виде произведения Приблизительно равная сезонная вариация указывает на существование аддитивной модели. Усиление сезонной вариации с возрастанием тренда указывает на существование мультипликативной модели. Построение аддитивной модели 1. Нахождение сглаж ур-ней динамич ряда методои скользящих средних 2. Оценка сезонной компоненты и ее корректировка 3. Элиминирование сезонной компоненты из исходных данных временного ряда 4. Построение уравнения линейного тренда по уровням ряда с элиминированием сезонности 5. расчет выровненных значений трендовой составляющей 6. расчет теоретич уровней ряда с учетом сезонности 7. расчет случайной компоненты, позволяющей оценить качество построенной модели
Исключение тенденции на основе метода отклонений от тренда
- прогноз у по тренду при t=p
- прогноз х исходя из уравнения тренда при t=p
yp прогнозное значение уровня ряда yn конечный уровень динамического ряда yt; xp и xp - то же по ряду xt
Автокорреляция в остатках. Критерий Дарбина-Уотсона в оценке качества уравнений, построенных по временным рядам
алгоритм выявления автокорреляции остатков на основе критерия Дарбина — Уотсона таков: 1) выдвигается гипотеза об отсутствии автокорреляции остатков; 2) альтернативные гипотезы состоят в наличии положительной или отрицательной автокорреляции в остатках; 3) затем по специальным таблицам определяются критические значения критерия Дарбина — Уотсона для заданного числа наблюдений, числа независимых переменных модели и уровня значимости; 4) по этим значениям числовой промежуток разбивают на пять отрезков. (2 из этих отрезков образуют зону неопределенности. 3 - нет оснований отклонять гипотезу об отсутствии автокорреляции, есть положительная автокорреляция, есть отрицательная автокорреляция. При попадании в зону неопределенности практически считают, что имеется автокорреляция остатков, и поэтому отклоняют гипотезу о ее отсутствии)
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 562; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.97.59 (0.01 с.) |



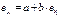
 - прогнозное значение у
- прогнозное значение у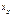
 - прогнозное значение х
- прогнозное значение х
 39. Исключение тенденции на основе метода последовательных разностей
39. Исключение тенденции на основе метода последовательных разностей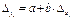


 40. Исключение тенденции на основе включения в модель регрессии по временным рядам фактора времени
40. Исключение тенденции на основе включения в модель регрессии по временным рядам фактора времени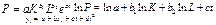

 Важной проблемой, естественно примыкающей к рассмотренным темам, является автокорреляция в остатках. Дело в том, что последовательность остатков может рассматриваться как временной ряд. Тогда возникает возможность построения зависимости этой последовательности остатков от времени. Согласно предпосылкам адекватности применения МНК, сами остатки должны быть случайными. В моделировании рядов динамики весьма распространена ситуация, когда остатки содержат циклические колебания. В этом случае каждое следующее значение остатков зависит от предшествующих, что и свидетельствует об автокорреляции остатков.Такая автокорреляция остатков бывает связана с исходными данными и вызвана ошибками измерения в значениях результативного признака. В других случаях автокорреляция остатков происходит из-за недостатков формулировки модели. Например, может отсутствовать фактор, оказывающий существенное воздействие на результат, влияние которого отражается в остатках. Тем самым остатки вполне могут оказаться автокоррелированными. Помимо фактора времени в качестве таких существенных факторов могут выступать лаговые значения переменных, включенных в модель. Может иметь место и такая ситуация, когда модель не учитывает несколько второстепенных по отдельности факторов, совместное влияние которых на результат уже оказывается существенным. Эта значимость проистекает в силу совпадения тенденций их изменения или фаз циклических колебаний.
Важной проблемой, естественно примыкающей к рассмотренным темам, является автокорреляция в остатках. Дело в том, что последовательность остатков может рассматриваться как временной ряд. Тогда возникает возможность построения зависимости этой последовательности остатков от времени. Согласно предпосылкам адекватности применения МНК, сами остатки должны быть случайными. В моделировании рядов динамики весьма распространена ситуация, когда остатки содержат циклические колебания. В этом случае каждое следующее значение остатков зависит от предшествующих, что и свидетельствует об автокорреляции остатков.Такая автокорреляция остатков бывает связана с исходными данными и вызвана ошибками измерения в значениях результативного признака. В других случаях автокорреляция остатков происходит из-за недостатков формулировки модели. Например, может отсутствовать фактор, оказывающий существенное воздействие на результат, влияние которого отражается в остатках. Тем самым остатки вполне могут оказаться автокоррелированными. Помимо фактора времени в качестве таких существенных факторов могут выступать лаговые значения переменных, включенных в модель. Может иметь место и такая ситуация, когда модель не учитывает несколько второстепенных по отдельности факторов, совместное влияние которых на результат уже оказывается существенным. Эта значимость проистекает в силу совпадения тенденций их изменения или фаз циклических колебаний.




