
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование модели парной регрессии для прогнозированияСодержание книги
Поиск на нашем сайте
Точечный прогноз осуществляется путем подстановки в найденной уравнение регрессии прогнозного значения Интервальный прогноз Определяется средняя ошибка прогнозного индивидуального значения y:
Строится доверительный интервал прогноза:
Визуальный анализ остатков Свойства остатков · Отсутствие связи между остатками и объясняющей переменной. · Отсутствие связи между остатками и предсказанными значениями. · Математическое ожидание остатков равно нулю. В выборке. · Остатки имеют постоянную дисперсию. Дисперсия остатков равна единице. Постоянство дисперсии остатков называют гомоскедастичностью остатков. Если же дисперсия остатков непостоянна, то имеет место гетероскедастичность остатков. · Остатки не коррелированны между собой. · Остатки распределены по нормальному закону распределения
Смысл и значение множественной регрессии в эконометрических исследованиях. Выбор Формы уравнения множественной регрессии Осн. цель – построение модели с неск. факторами, определив при этом влияние каждого из них в отдельности совокупности их воздействия на результативные признаки. М. p. — метод многомерного анализа, посредством к-рого зависимая переменная (или критерий) Y связывается с совокупностью независимых переменных (или предикторов) X посредством линейного уравнения: Y' = а + b1Х1 + b2Х2 +... + bkXk. 1. Получение наилучшего линейного ур-я прогноза. 2. Контроль за смешиванием перемен (факторов). 3. Оценка вклада определенной совокупности переменных. 4. Объяснение сложного на вид многомерного комплекса взаимосвязей. 5. Проведение дисперсионного и ковариационного анализов посредством кодирования уровней независимых переменных. Наиболее часто используются следующие функции: линейная степенная функция показательная функция экспонента гипербола Отбор факторов в уравнение множественной регрессии · в модель нужно включать только существенные факторы, непосредственно формирующее результат · факторы должны быть количественно измерены · факторы не должны находиться в тесной взаимосвязи друг с другом (значение коэффициента корреляции между факторами, входящими в модель должно быть менее 0,7) Отбор факторов основан на: · теоретическом анализе взаимосвязи результата с кругом факторов · количественном анализе (на основе матрицы парных коэффициентов корреляции, матрицы частных коэффициентов корреляции, с помощью стандартизованных коэффициентов регрессии, на основе F, t- критериев Оценка параметров уравнения множественной регрессии Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). При этом нелинейные функции приводятся к линейному виду по параметрам.
Абсолютные и относительные показатели силы связи в модели множественной регрессии Абсолютные - показывают, на сколько единиц в среднем изменяется результативный признак при изменении рассматриваемого факторного признака на одну единицу при условии, что остальные факторы зафиксированы на среднем уровне и не меняются Относительны е · частные коэф эластичности; показывают, на сколько процентов в среднем меняется результативный признак при изменении рассматриваемого факторного признака на один процент при условии, что остальные факторы зафиксированы на среднем уровне и не меняются. Параметры · стандартизованные коэффициенты регрессии Множественный коэффициент корреляции и коэффициент детерминации Коэффициент множественной детерминации (R2) показывает долю вариации результативного признака, за счет вариации включенных в модель факторов:
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.38.67 (0.007 с.) |

 :
: 


 ;
; ;
; ;
; ;
; .
.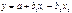

 19. Построение уравнения регрессии в стандартизованном масштабе
19. Построение уравнения регрессии в стандартизованном масштабе

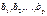 в степенной модели являются частными коэффициентами эластичности.
в степенной модели являются частными коэффициентами эластичности. ,
,

 Коэффициент (индекс) множественной корреляции (R) – корень квадратный из коэффициента множественной детерминации
Коэффициент (индекс) множественной корреляции (R) – корень квадратный из коэффициента множественной детерминации  :
:


