
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гетероскедастичность - понятие, проявление и меры устраненияСодержание книги
Поиск на нашем сайте
Г -означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК Основные предпосылки МНК: n случайный характер остатков n нулевая средняя остатков, не зависящая от фактора x n гомоскедастичность (дисперсия каждого отклонения одинакова для всех значений x) n отсутствие автокорреляции остатков n остатки должны подчиняться нормальному распределению Меры по устранению гетероскедастичности · Увеличение числа наблюдений · Изменение функциональной формы модели · Разделение исходной совокупности на качественно-однородные группы и проведение анализа в каждой группе · Использование фиктивных переменных, учитывающих неоднородность · Исключение из совокупности единиц, дающих неоднородность Оценка гетероскедастичности с помощью метода Гольдфельда Квандта · Все наблюдения упорядочивают по мере возрастания какого-либо фактора, который, как предполагается, оказывает влияние на возрастание дисперсии остатков. · Упорядоченную совокупность делят на три группы, причем первая и последняя должны быть равного объема с числом единиц, больших, чем число параметров модели регрессии. Число отобранных единиц обозначим k · По первой и третьей группе находят параметры уравнений регрессии и остатки по ним. · df 1= df 2= k-m-1 Использование коэффициента корреляции рангов Спирмэна для проверки наличия гетероскедастичности в остатках Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента. Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле:.
Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции. Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных, но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности Использование тестов Уайта, Парка, Глейзера при анализе гетероскедастичности в остатках
k – какое-либо число, например, k = – 1; – 0,5; 0,5; 1 Уайта: Содержательный смысл теста в том, что часто гетероскедастичность модели вызвана зависимостью (возможно довольно сложной) дисперсий ошибок от признаков. Реализуя эту идею, Уайт предложил метод тестирования гипотезы H0 без каких-либо предположений о структуре гетероскедастичности. Сначала к исходной модели применяется обычный метод наименьших квадратов и находятся остатки регрессии e(t), t=1,…n. Затем осуществляется регрессия квадратов этих остатков e(t)2 на все признаки, их квадраты, попарные произведения и константу. Тогда при гипотезе H0 величина nR2 асимптотически имеет распределение x2(N-1), где R2 — коэффициент детерминации, а N — число регрессоров второй регрессии. Плюс данного теста — его универсальность. Минусы: 1) если гипотеза H0отвергается, то никаких указаний на функциональную форму гетероскедастичности мы не получаем; 2) несомненным минусом является поиск вслепую вида регрессии
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.135 (0.01 с.) |

 Используя данные об остатках моделей первой и третьей группы, рассчитывают фактическое значение F -критерия
Используя данные об остатках моделей первой и третьей группы, рассчитывают фактическое значение F -критерия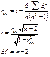
 Парка:
Парка: Глейзера:
Глейзера:



