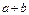Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение обобщенного метода наименьших квадратов (ОМНК) для случая гетероскедастичности остатков.Содержание книги
Поиск на нашем сайте
В этом плане невозможность или нецелесообразность использования традиционного МНК по причине проявляющейся в той или иной степени гетероскедастичности привели к разработке ОМНК Выдвигается гипотеза, что дисперсия остатков пропорциональна x2
Оценка параметров полученного т.о. нового уравнения с гомоскедастичными остатками будет сводиться к взвешенному МНК (по существу это и есть ОМНК). новые переменные уже получают иное экономическое содержание.
Мультиколлинеарность факторов – понятие, проявление и меры устранения Симптомы мультиколлинеарности · Завышенное значение коэф детерминации · Высокие стандартные ошибки для коэффициентов регрессии · Широкие доверительные интервалы · Низкое значение t-критерия · Появление при коэффициентах регрессии знаков, противоположных ожидаемым Меры по устранению мультиколлинеарности · Удаление из модели переменных с высоким коэффициентом парной корреляции между факторами, если это не противоречит теории, положенной в основу построения модели · Увеличение числа наблюдений · Изменение функциональной формы модели · Использование априорной информации · Построение моделей по отклонениям от средней величины · Использование специальных методов обработки временных рядов Специфика временного ряда как источника данных в эконометрическом моделировании Временной (динамический) ряд – это ряд последовательно расположенных во времени числовых значений соответствующего показателя Элементы временного ряда: · уровни ряда (yt)- числовые значения того или иного показателя; · время (t). Виды временных рядов: · моментные, если время задано моментами; · интервальные, если время задано интервалами. · Модели на основе рядов динамики · Модели изолированного динамического ряда. · Модели системы взаимосвязанных рядов динамики. · Модели автрегрессии. · Модели с распределенным лагом Компоненты временного ряда · Тенденция (T) · Периодические колебания (P) · Случайные колебания (E) yt = f (T,P,E) Автокорреляция уровней временного ряда и ее последствия
Последствия: · Оценки параметров, оставаясь линейными не смещенными, перестают быть эффективными, они перестают обладать свойствам наилучших линейных несмещенных оценок · Дисперсии оценок являются смещенными. · Зачастую дисперсии являются заниженными, что привод к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые могут ими и не являться. · Коэф. регрессии и детерминации м.б. не верными, следовательно ухудшаются прогнозные качества модели.
Моделирование тенденции временных рядов Метод аналитического выравнивания сводится к замене фактических данных сглаженными, определенными по выбранной математической функции. При этом, уровни временного ряда рассматриваются как функция от времени: yt = f(t) Этапы построения модели тенденции (уравнения тренда) · Выбор математической функции, описывающей тенденцию · Оценка параметров модели · Проверка адекватности выбранной функции и оценка точности модели · Расчет точечного и интервального прогнозов Виды математических функций, описывающих тенденцию · Функции с монотонным характером возрастания (убывания) и отсутствием пределов роста (сниж-я) · Кривые с насыщением, т. е. устанавливается нижняя или верхняя граница изменения уровней ряда · S -образные кривые, т. е. кривые с насыщением, имеющие точку перегиба Оценивание параметров в уравнениях тренда Уравнения трендов: · линейная: · параболическая: · степенная: · гипербола: · показательная: ·
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.38.184 (0.007 с.) |


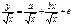 новое уравнение в преобразованных переменных, в котором уже остатки будут гомоскедастичны. Сами новые переменные — это взвешенные старые (исходные) переменные
новое уравнение в преобразованных переменных, в котором уже остатки будут гомоскедастичны. Сами новые переменные — это взвешенные старые (исходные) переменные


 Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда
Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда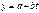


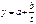
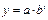
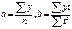
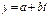 экспонента:
экспонента: