
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные показатели динамики экономических явленийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
20. Сглаживание временных рядов с помощью скользящих средних Методы «механического» сглаживания. Метод скользящей средней. Данный метод применяется для характеристики тенденции развития исследуемой статистической совокупности и основан на расчете средних уровней ряда за определенный период. Последовательность определения скользящей средней: - устанавливается интервал сглаживания или число входящих в него уровней. Если при расчете средней учитываются три уровня, скользящая средняя называется трехчленной, пять уровней – пятичленной и т.д. Если сглаживаются мелкие, беспорядочные колебания уровней в ряду динамики, то интервал (число скользящей средней) увеличивают. Если волны следует сохранить, число членов уменьшают. - Исчисляют первый средний уровень по арифметической простой: y1 = Sy1/m, где y1 – I-ый уровень ряда; m – членность скользящей средней. - первый уровень отбрасывают, а в исчисление средней включают уровень, следующий за последним уровнем, участвующем в первом расчете. Процесс продолжается до тех пор, пока в расчет y будет включен последний уровень исследуемого ряда динамики yn.
- по ряду динамики, построенному из средних уровней, выявляют общую тенденцию развития явления.
Отрицательной стороной использования метода скользящей средней является образование сдвигов в колебаниях уровней ряда, обусловленных «скольжением» интервалов укрупнения. Сглаживание с помощью скользящей средней может привести к появлению «обратных» колебаний, когда выпуклая «волна» заменяется на вогнутую. В последнее время стала рассчитываться адаптивная скользящая средняя. Ее отличие состоит в том, что среднее значение признака, рассчитываемое также как описано выше, относится не к середине ряда, а к последнему промежутку времени в интервале укрупнения. Причем предполагается, что адаптивная средняя зависит от предыдущего уровня в меньшей степени, чем от текущего. То есть., чем больше промежутков времени между уровнем ряда и средним значением, тем меньшее влияние оказывает значение этого уровня ряда на величину средней.
21. Применение простых скользящих средних Распространенным приемом при выявлении и анализе тенденции развития явля- ется сглаживание временного ряда. Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые в мень- шей степени подвержены колебаниям. Это способствует более четкому проявлению тенденции развития. Методы сглаживания можно условно разделить на два класса, опирающиесяна раз- личные подходы: • аналитический подход; • алгоритмический подход. Аналитический подход основан на допущении, что исследователь может задать общий вид функции, описывающей регулярную, неслучайную составляющую. Например, на основе визуального и содержательного экономического анализа динамики временного ряда предполагается, что трендовая составляющая может быть описана с помощью пока- зательной функции: t yt = a ⋅b. Тогда на следующем этапе будет произведена статистическая оценка неизвестных коэффициентов модели, а затем определены сглаженные значения уровней временного ряда путем подстановки соответствующего значения временного параметра t в получен- ное уравнение (заданное в явном аналитическом виде). Процедуры моделирования, опи- рающиеся на этот подход, рассматриваются в следующей главе. При использовании алгоритмического подхода отказываются от ограничительного допущения, свойственного аналитическому. Процедуры этого класса не предполагают описания динамики неслучайной составляющей с помощью единой функции, они предос- тавляют исследователю лишь алгоритм расчета неслучайной составляющей в любой за- данный момент времени t. Методы сглаживания временных рядов с помощью скользящих средних относятся к этому подходу. Иногда скользящие средние применяют как предварительный этап перед модели- рованием тренда с помощью процедур, относящихся к аналитическому подходу. Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса, и поэтому служат важным инструментом при фильтрации компонент временного ряда. Алгоритм сглаживания по простой скользящей средней может быть представлен в виде следующей последовательности шагов: 1. Определяют длину интервала сглаживания l, включающего в себя l последователь- ных уровней ряда (l < n). При этом надо иметь в виду, что чем шире интервал сглажи- вания, тем в большей степени взаимопогашаются колебания, и тенденция развития но- сит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания. 2. Разбивают весь период наблюдения на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1. 3. Рассчитывают средние арифметические из уровней ряда, образующих каждый участок. 4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.
Процедура сглаживания приводит к к устранению периодических колебаний во временном ряду, если длина интервалов берется равной (или кратной) периоду колебаний. Для устранения сезонных колебаний часто требуется 4-х или 12-ти членные скользящие средние.
22. Использование взвешенных скользящих средних Иногда, при построении скользящей средней, некоторые значение исходной функции целесообразно сделать более значимым. Например, если предполагается, что внутри интервала сглаживания имеет место нелинейная тенденция, или в случае временных рядов, последние — более актуальные данные могут быть весомее предыдущих. Бывает, что исходная функция многомерна, то есть представлена сразу несколькими связанными рядами. В этом случае, может возникнуть необходимость объединить в итоговой функции скользящей средней все полученные данные. Например, временные ряды биржевых цен, обычно, для каждого момента времени представлены как минимум двумя значениями — ценой сделки и её объёмом. Необходим инструмент для вычисления скользящей средней цены, взвешенной по объёму. В этих и подобных случаях применяются взвешенные скользящие средние.
23. Применение моделей кривых роста в экономическом прогнозировании На практике для описания тенденции развития явления широко используются мо- дели кривых роста, представляющие собой различные функции времени y = f(t). При та- ком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени. Правильно выбранная модель кривой роста должна соответствовать характеру из- менения тенденции исследуемого явления. Кривая роста позволяет получить выровнен- ные или теоретические значения уровней динамического ряда. Это те уровни, которые на- блюдались бы в случае полного совпадения динамики явления с кривой. Прогнозирование на основе модели кривой роста базируется на экстраполяции, т. е. на продлении в будущее тенденции, наблюдавшейся в прошлом. При этом предполагается, что во временном ряду присутствует тренд, характер развития показателя обладает свойством инерционности, сложившаяся тенденция не должна претерпевать существенных изменений в течение периода упреждения. Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы: 1) выбор одной или нескольких кривых, форма которых соответствует характеру изменения временного ряда; 2) оценка параметров выбранных кривых; 3) проверка адекватности выбранных кривых прогнозируемому процессу, оценка точности моделей и окончательный выбор кривой роста; 4) расчет точечного и интервального прогнозов. В настоящее время в литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания экономических временных рядов. Кривые роста условно могут быть разделены на три класса в зависимости от того, какой тип динамики развития они хорошо описывают. К I типу относятся функции, используемые для описания процессов с монотонным характером тенденции развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей, например, для большинства натуральных показа- телей промышленного производства. Ко II классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. С такими процессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при ис- следовании эффективности использования ресурсов и т.д. Примерами показателей, для которых могут быть указаны пределы роста, являются среднедушевое потребление оп- ределенных продуктов питания, расход удобрений на единицу площади и т.п. Функции, относящиеся ко II классу, называются кривыми насыщения. Если кривые насыщения имеют точки перегиба, то они относятся к III типу кривых роста — к S-образным кривым. Эти кривые описывают как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, другой — с замедлением. S-образные кривые находят применение в демографических исследованиях, в стра- ховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции. Вопрос о выборе кривой является основным при выравнивании ряда.
24. Оценка параметров в модели кривых роста. МНК
25. Методы выбора кривых роста Существует несколько практических подходов, облегчающих процесс выбора фор- мы кривой роста. Наиболее простой путь — визуальный анализ, опирающийся на изучение графиче- ского изображения временного ряда. Подбирают такую кривую роста, форма которой со- ответствует фактическому развитию процесса. Если на графике исходного ряда тенденция развития недостаточно четко просматривается, то можно провести некоторые стандарт- ные преобразования ряда (например, сглаживание), а потом подобрать функцию, отве- чающую графику преобразованного ряда. В современных пакетах статистической обра- ботки имеется богатый арсенал стандартных преобразований данных и широкие возмож- ности для графического изображения, в том числе в различных масштабах. Все это позво- ляет существенно упростить для исследователя проведение данного этапа. В статистической литературе описан метод последовательных разностей, помо- гающий при выборе кривых полиномиального типа. Этот метод применим при выполне- нии следующих предположений: уровни временного ряда могут быть представлены в виде суммы систематической составляющей и случайной компоненты, подчиненной нормаль- ному закону распределения с математическим ожиданием, равным 0, и постоянной дис- персией. Метод предполагает вычисление первых, вторых и т. д. разностей уровней ряда.
Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома. Существенную помощь при выборе кривых роста из более широкого класса функ- ций может оказать метод характеристик прироста. Процедура выбора кривых с использованием этого метода включает следующие шаги: 1) выравнивание ряда с помощью скользящей средней; 2) определение средних приростов; 3) вычисление производных характеристик прироста. Для многих видов кривых были найдены такие преобразования приростов, которые линейно изменялись относительно t или были постоянны. В связи с этим исследование рядов характеристик приростов часто оказывает существенную помощь при определении законов развития исходных временных рядов. Данный метод является более универсальным по сравнению с методом последова- тельных разностей. Однако чаще всего на практике к выбору формы кривой подходят исходя из значе- ний критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровней от расчетных, получаемых выравниванием. Из рассматриваемых кри- вых предпочтение будет отдано той, которой соответствует минимальное значение крите- рия, т.к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений. Используя этот подход, следует иметь в виду ряд моментов. Во-первых, к ряду, состоящему из m точек можно подобрать многочлен (полином) степени (m – 1), проходящий через все m точек. Во-вторых, существует множество многочленов более высоких степеней, также проходящих через все эти точки. Для этих многочленов значение критерия будет равно 0, однако очевидно, что такая кривая не слишком пригодна как для выделения тенденции, так и для целей прогнозирования. Также следует учитывать, что за счет роста сложности кривой можно увеличить точность описания тренда в прошлом, однако доверительные интервалы при прогнозиро- вании будут существенно шире, чем у более простых кривых при одинаковом периоде уп- реждения, например, за счет большего числа параметров.
26. Этапы прогнозирования экономических явлений и процессов: 1. Постановка задачи и сбор необходимой информации 2. Первичная обработка исходных данных 3. Определение круга возможных моделей прогнозирования 4. Оценка параметров моделей. 5. Исследование качества выбранных моделей, адекватности их реальному процессу и выбор лучшей из моделей 6. Построение прогноза 7. Содержательный анализ полученного прогноза
|
|||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.32.6 (0.015 с.) |

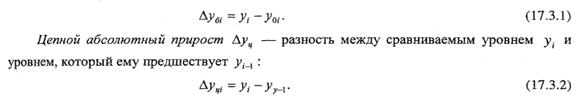 Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень показателя изучаемого периода ниже базисного.
Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов ^Д^,,, равна базисному абсолютному приросту последнего периода ряда динамики A^g„:
Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень показателя изучаемого периода ниже базисного.
Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов ^Д^,,, равна базисному абсолютному приросту последнего периода ряда динамики A^g„:
 Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Базисные темпы роста Tpg исчисляются делением сравниваемого уровня у, на уровень, принятый за постоянную базу сравнения уо,:
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Базисные темпы роста Tpg исчисляются делением сравниваемого уровня у, на уровень, принятый за постоянную базу сравнения уо,:
 Цепные темпы роста Трб исчисляются делением сравниваемого уровняв, на предыдущий уровень y0i:
Цепные темпы роста Трб исчисляются делением сравниваемого уровняв, на предыдущий уровень y0i:
 Если темп роста больше единицы (или 100%), то это указывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) указывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился изучаемый уровень по сравнению с уровнем, принятым за базу сравнения.
Базисный темп прироста Tg вычисляется делением сравниваемого базисного абсолютного прироста Ауд на уровень, принятый за постоянную базу сравнения уoi:
Если темп роста больше единицы (или 100%), то это указывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) указывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился изучаемый уровень по сравнению с уровнем, принятым за базу сравнения.
Базисный темп прироста Tg вычисляется делением сравниваемого базисного абсолютного прироста Ауд на уровень, принятый за постоянную базу сравнения уoi:
 Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня ряда динамики.
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала.
Вычисляются темпы наращивания Тн делением цепных абсолютных приростов Av,
на уровень, принятый за постоянную базу сравнения уц,:
Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня ряда динамики.
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала.
Вычисляются темпы наращивания Тн делением цепных абсолютных приростов Av,
на уровень, принятый за постоянную базу сравнения уц,:
 Из преобразований в формуле (17.3.10) следует, что темпы наращивания можно непосредственно определять по базисным темпам роста:
Из преобразований в формуле (17.3.10) следует, что темпы наращивания можно непосредственно определять по базисным темпам роста:










