
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя арифметическая и ее свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной. Средняя арифметическая простая (невзвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным.
Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по нескольку раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. Свойства средней арифметической. Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчетах: 1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты. 2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю. 3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С. 4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину. 5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз. 6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится.
Другие виды средних величин Средняя гармоническая взвешенная:
где Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид:
Для иллюстрации области ее применения воспользуемся упрощенным условным примером. Предположим, в автохозяйстве эксплуатируются два электромобиля разных моделей, работающих на однотипных подзаряжаемых за ночь аккумуляторных батареях. Первый электромобиль расходует на 1 км пути 1,0 кВт ч электроэнергии, второй - 0,6 кВт- ч. Каков средний расход электроэнергии на 1 пройденный километр?
На первый взгляд решение этой задачи заключается в осреднении индивидуальных значений потребления электроэнергии по двум электромобилям, т.е. (1,0 + 0,6): 2 = 0,8 кВт ч. Проверим обоснованность такого подхода на примере одного дня работы машин, в течение которого они расходуют один заряд аккумулятора, предположим, 60,0 кВт ч (как будет показано ниже, конкретная цифра значения не имеет). За этот день первая машинам пройдет 60 км (60,0/1,0), пробег отарой составит 100 км (60,0/0,6), т.е. в сумме- 160 км. Если же заменить индивидуальные значения признака их предполагаемым средним значением, то общий пробег, выступающий в данном случае в качестве определяющего показателя, сократится до 150 км (60,0/0,8 + 60,0/0,8). Следовательно, полученная средняя рассчитана неверно. Средняя геометрическая. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая:
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста. Средняя квадратическая. Воснове вычислений ряда сводных расчетных показателей лежит средняя квадратическая:
Наиболее широко этот вид средней используется при расчете показателей вариации.
Структурные средние(мода и медиана). В отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, структурные средние выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач. Модой ( Медианой ( Ранжированный ряд — ряд, расположенный в порядке возрастания или убывания значений признака. Для определения медианы сначала определяют ее местов ряду, используя формулу:
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую из двух срединных значений. Мода применяется при экспертных оценках, при определении наиболее ходовых размеров обуви, одежды, что учитывается при планировании их производства. Медиана используется при статистическом контроле качества продукции и технологического процесса на промышленных предприятиях; при изучении распределения семей по величине дохода и др. Мода и медиана имеют преимущество перед средней арифметической для ряда распределения с открытыми интервалами.
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 3112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.185.58 (0.01 с.) |

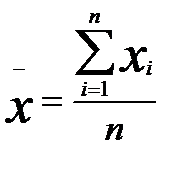

 ,
,

 .
.
 - взвешенная.
- взвешенная. - невзвешенная;
- невзвешенная; - взвешенная.
- взвешенная. ) называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
) называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду). ) называется значение признака, которое лежитв середине ранжированного ряда и делит этот ряд на две равныепо численности части.
) называется значение признака, которое лежитв середине ранжированного ряда и делит этот ряд на две равныепо численности части.



