
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод расчета «устойчивой прочности» гибких сжатых железобетонных элементов с использованием понятия условной критической силы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод «устойчивой прочности» относится к методам второй группы. Если принять, что упругая линия внецентренно сжатого элемента с шарнирными закреплениями по концам имеет вид синусоиды, т.е.
где f – прогиб элемента в середине пролета, то дополнительный изгибающий момент, вызванный действием продольного изгиба, составит:
Тогда полный прогиб а в общем случае можно определить из уравнения:
где: а0 – начальный прогиб, вызванный действием поперечной нагрузки; Полный момент в середине пролета составит: где MSd,0 – момент в середине пролета от поперечной нагрузки. где: Принимая во внимание, что Значение критической силы Ncrit для железобетонного элемента можно рассматривать как сумму критических сил для бетонного сечения Ncrit,c и арматуры Ncrit,s. На основании экспериментальных исследований с учетом специфики железобетона (неупругой работы, особенно в стадиях, близких к разрушению) для определения критической силы Ncrit нормы используют формулу, предложенную Е.А. Чистяковым и К.Э. Талем: где: Jc и Js – соответственно моменты инерции бетонного сечения площадью Ас и арматуры As; При применении данной формулы значения e0/h должны приниматься не менее граничных значений: Ползучесть бетона учитывается коэффициентом klt, равным: где: NSd,lt – продольная сила от длительно действующей части нагрузки; j(¥, t0) – предельное значение коэффициента ползучести для бетона. Влияние гибкости сжатого элемента несмещаемого каркаса на его несущую способность учитывают путем расчета его прочности как внецентренно сжатого элемента с учетом увеличения изгибающих моментов для сечений у концов рассматриваемого элемента и в середине трети его длины соответственно по формулам: , где М1 – момент у рассматриваемого конца элемента; М2 – максимальный момент в пределах средней трети длины элемента. Для ступенчатых колонн за отдельный элемент принимают часть колонны с постоянными размерам поперечного сечения. где Mmax – наибольший из изгибающих моментов в опорных сечениях колонн (всегда положительный); Mmin – меньший момент (может быть обоих знаков). Полный расчетный эксцентриситет продольной силы NSd, определенный с учетом продольного изгиба, составит: где: ea – случайный эксцентриситет, принимаемый в зависимости от типа конструкции, длины элемента lcol и высоты сечения (по большему значению): ea = 10 мм – для монолитных конструкций стен, оболочек, а также 20 мм – для сборных элементов, за исключением стен и оболочек; здесь MSd – полный расчетный момент в сечении, вычисленный по деформационному расчету или с приближенным учетом продольного изгиба. Расчетная длина колонн смещаемых каркасов определяется в соответствии с ранее изложенными положениями. При гибкости l≤22 влияние продольного изгиба можно не учитывать. Расчетный изгибающий момент M1,sd по концам колонны определяют по формуле:
где:
Изгибающие моменты от смещения рамы с учетом продольного изгиба Величину коэффициента
где:
32.Полный расчетный эксцентриситет продольной силы (с учетом продольного изгиба и случайного эксцентриситета). Полный расчетный эксцентриситет при применении методов первой группы определяют по формуле:
где: e0 – начальный эксцентриситет продольной силы, определяемый по формуле: ea – дополнительный незамеренный эксцентриситет, обусловленный несовершенствами изготовления и возведения конструкции, определяемый по формуле: здесь: l0 – расчетная длина элемента; e2 – дополнительный эксцентриситет, обусловленный продольным изгибом элемента. Для сжатых элементов прямоугольного или круглого сечения, удовлетворяющих условиям l < 140 и l0 ³ 0,1h, максимальный прогиб e2 допускается определять по упрощенной формуле, полученной по т.н. методу «модельной стойки»: где: k1 = 1для l > 35. Кривизну сжатого элемента в расчетном сечении допускается определять по упрощенной формуле, полученной в предположении, что сжатая и растянутая арматура получают деформации e sy, соответствующие пределу текучести Тогда кривизна сечения: где: k2 – коэффициент, учитывающий изменение кривизны (1/r) с возрастанием продольной силы NSd, определяемый по формуле: здесь: Nud – усилие, воспринимаемое сечением при осевом приложении продольного усилия
Nbal – продольная сила, соответствующая наибольшему изгибающему моменту. Для прямоугольных симметрично армированных сечений:
При расчетах можно принимать k2 = 1, что обеспечивает большую безопасность конструкции; k j – коэффициент, учитывающий влияние ползучести бетона. Для бетонов классов по прочности выше С40/50 а для бетонов меньших классов допускается принимать k j = 1,0.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.63 (0.008 с.) |

 (10.17)
(10.17)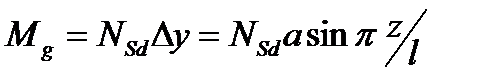 . (10.18)
. (10.18) , (10.19)
, (10.19) – момент от единичной силы, приложенной в середине пролета по направлению искомого перемещения.
– момент от единичной силы, приложенной в середине пролета по направлению искомого перемещения. , (10.20)
, (10.20) , (10.21)
, (10.21) . (10.22)
. (10.22) – это, по существу, Эйлерова критическая сила Ncrit, указанная формула может быть записана в виде:
– это, по существу, Эйлерова критическая сила Ncrit, указанная формула может быть записана в виде: . (10.23)
. (10.23) , (10.24)
, (10.24) . (10.25)
. (10.25) и
и  . (10.26)
. (10.26)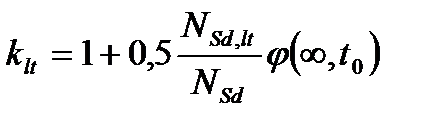 , (10.27)
, (10.27) , но не менее М1, (10.28)
, но не менее М1, (10.28) , (10.29)
, (10.29) ,
,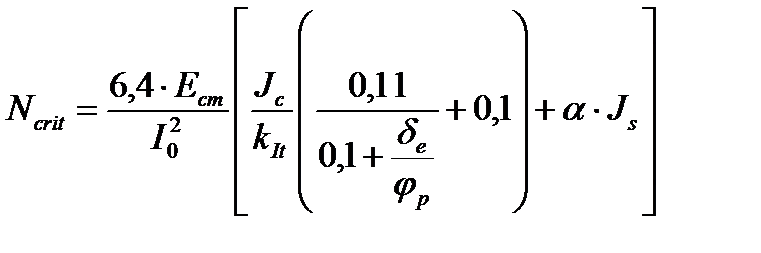
 , (10.32)
, (10.32) ,
, 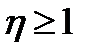 , (10.33)
, (10.33) – в плосконапряженных (балках-стенках) и каркасных системах с несмещаемыми узлами; lcol – расстояние между точками закрепления элемента; для консольных элементов lcol = l0;
– в плосконапряженных (балках-стенках) и каркасных системах с несмещаемыми узлами; lcol – расстояние между точками закрепления элемента; для консольных элементов lcol = l0; – в каркасных системах со смещаемыми узлами; для элементов «n»-го этажа считая от верхнего;
– в каркасных системах со смещаемыми узлами; для элементов «n»-го этажа считая от верхнего; , здесь h – высота сечения элемента в плоскости действия расчетного момента;
, здесь h – высота сечения элемента в плоскости действия расчетного момента; – эксцентриситет, определяемый из статического расчета:
– эксцентриситет, определяемый из статического расчета: (10.34)
(10.34) - расчетный изгибающий момент у рассматриваемой опоры, определенный из линейно-упругого расчета от действия нагрузок, не вызывающих смещение каркаса;
- расчетный изгибающий момент у рассматриваемой опоры, определенный из линейно-упругого расчета от действия нагрузок, не вызывающих смещение каркаса; - то же, но от действия нагрузок, вызывающих смещение каркаса;
- то же, но от действия нагрузок, вызывающих смещение каркаса; - коэффициент увеличения момента в гибких сжатых элементах смещаемых каркасов.
- коэффициент увеличения момента в гибких сжатых элементах смещаемых каркасов. предпочтительно определять, рассматривая упругую стержневую систему и принимая во внимание влияние продольных сил на реакции от единичных перемещений конечных элементов.
предпочтительно определять, рассматривая упругую стержневую систему и принимая во внимание влияние продольных сил на реакции от единичных перемещений конечных элементов. (10.35)
(10.35) - сумма условных критических сил во всех колоннах, сопротивляющихся смещению;
- сумма условных критических сил во всех колоннах, сопротивляющихся смещению; - сумма всех расчетных вертикальных сил в колоннах рассматриваемого этажа.
- сумма всех расчетных вертикальных сил в колоннах рассматриваемого этажа. , (10.36)
, (10.36) ; (10.37)
; (10.37) , (10.38)
, (10.38) – угол отклонения (рад) сжатого элемента от вертикали, принимаемый не менее n min = 1/200;
– угол отклонения (рад) сжатого элемента от вертикали, принимаемый не менее n min = 1/200; , (10.39)
, (10.39)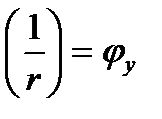 – кривизна сжатого элемента в расчетном сечении, определяемая из расчета по деформационной модели;
– кривизна сжатого элемента в расчетном сечении, определяемая из расчета по деформационной модели; для 15 £ l £ 35;
для 15 £ l £ 35; .
. , (10.40)
, (10.40) , (10.41)
, (10.41) (10.42)
(10.42) (10.43)
(10.43) , (10.44)
, (10.44)


