
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии исчерпания прочности железобетонной конструкции по нормальному сечению в общем деформационном методеСодержание книги
Поиск на нашем сайте
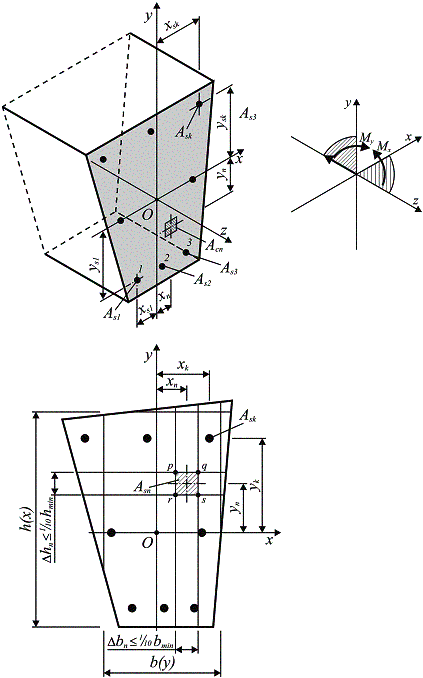
При использовании деформационной расчетной модели критерием исчерпания прочности железобетонной конструкции по нормальному сечению принято условие достижения сжатым бетоном и (или) растянутой арматурой предельных значений относительных деформаций, установленных нормативными документами. При решении указанных уравнений используют либо правила точного интегрирования, либо прибегают к численному интегрированию (суммированию) напряжений, действующих по элементарным площадкам, выделенным в пределах расчетного сечения. Наиболее распространенным считается метод численного интегрирования (суммирования), в котором бетонное сечение мысленно разбивают на отдельные малые участки площадью Acn, как правило, прямоугольной формы, дополненные по необходимости треугольными или трапециевидными участками. В упрощенных моделях принимают допущение о том, что напряжения scn в пределах каждого выделенного элементарного участка бетона постоянны и равны напряжениям на уровне его центра тяжести (рис. 9.1). Поэтому относительные деформации ecn рассчитывают на уровне центра тяжести каждого элементарного участка. Считается, что допущение о постоянстве напряжений в пределах элементарного участка не вносит существенной погрешности в расчеты, если его размеры не превышают 1/10 соответствующего размера сечения. Для каждого «n»-го элементарного участка бетона фиксируют его площадь Acn и координаты центра тяжести xn, yn (расстояния до соответствующих осей, рис. 9.1). Каждому арматурному стержню присваивают свой номер, а также фиксируют его площадь Ask и положение центра тяжести xk, yk. Тогда обозначив Mx = (MSd,x + NSdex), My = (MSd,y + NSdey) и переходя к численному интегрированию условия равновесия могут быть записаны:
Учитывая то обстоятельство, что напряжения и относительные деформации на рассматриваемом уровне нагружения конструкции связаны секущим модулем деформаций, определяемым из диаграммы деформирования, можно записать:
Разбиение поперечного сечения на элементарные участки при расчете на действие изгибающих моментов и продольных сил
где Условия равновесия с учетом этого запишутся в виде:
Подставив в условия равновесия сечения уравнения, описывающие распределение относительных деформаций в бетоне и арматуре, получаем:
Выполняя преобразования уравнений, получаем систему расчетных уравнений относительно неизвестных ez, jx, jy:
где - осевая жесткость, зависящая от уровня нагружения и геометрических характеристик сечения;
- изгибно-осевая жесткость, отражающая взаимное влияние продольного сжатия (растяжения) и изгиба по направлению оси х;
- изгибная жесткость в направлении оси х; - изгибно-осевая жесткость по направлению оси у; - жесткость, отражающая взаимное влияние изгиба в направлении осей х и у; - изгибная жесткость в направлении оси у. Систему уравнений удобно решать в матричной форме:
ez – относительная продольная деформация (по линии продольной оси z элемента); jx, jy – кривизны продольной оси элемента в плоскостях, совпадающих с осями х и у. Систему уравнений решают итерационным методом. 27.Расчетная схема и расчетные уравнения для упрощенного деформационного метода определения прочности сечений прямоугольного профиля с двойным армированием. Для таврового (двутаврового) сечения с двойным армированием:
Если условие выполняется, это означает, что нейтральная ось располагается в пределах полки и сечение рассчитывают как прямоугольное. Если условие не выполняется, производят расчет таврового сечения, для которого равнодействующая усилий в сжатом бетоне определяется по формулам:
Тогда уравнение моментов относительно центра тяжести площади растянутой арматуры в общем случае можно записать в виде:
При подборе продольной арматуры положение нейтральной оси определяется из условия Момент, воспринимаемый полкой определяется из уравнений:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.136 (0.008 с.) |

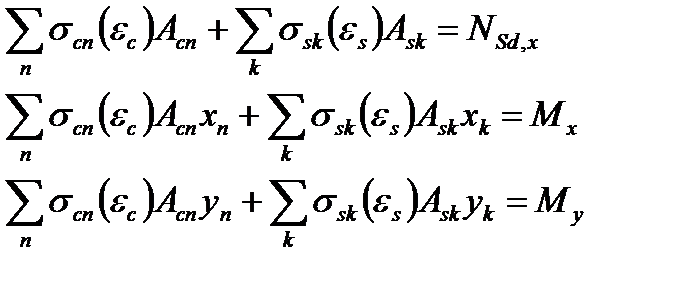
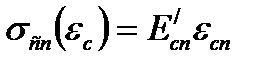
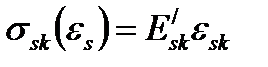
 ,
, 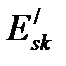 – численные значения модуля деформаций соответственно для бетона и арматуры, определяемые из диаграммы деформирования на соответствующем уровне нагружения.
– численные значения модуля деформаций соответственно для бетона и арматуры, определяемые из диаграммы деформирования на соответствующем уровне нагружения.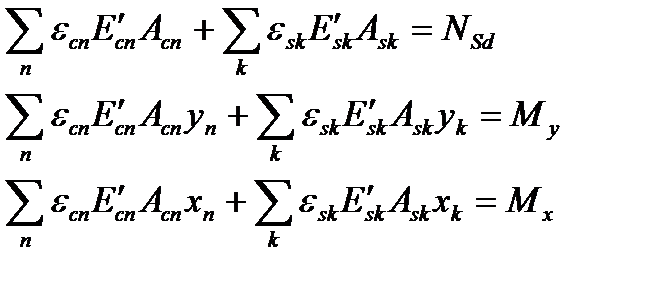
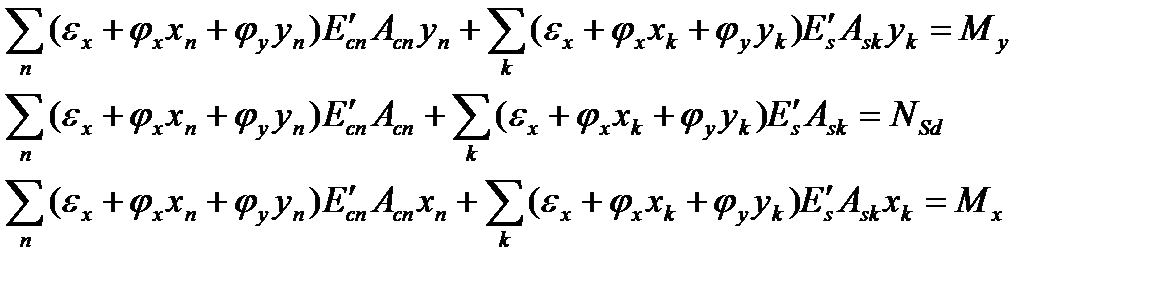
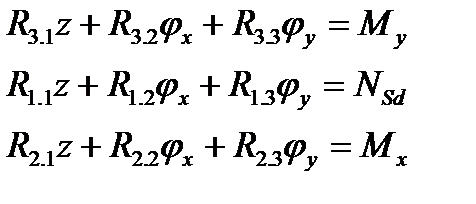
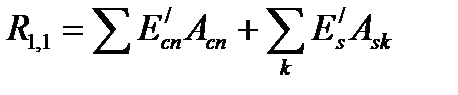
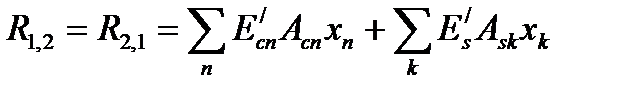
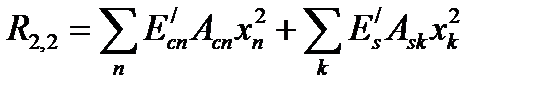


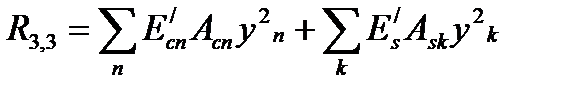
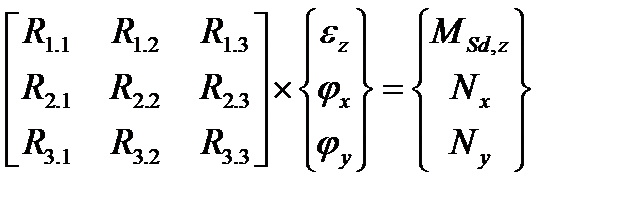
 –вектор-столбец усилий, вызванных действием расчетных воздействий в рассматриваемом сечении конструкции;
–вектор-столбец усилий, вызванных действием расчетных воздействий в рассматриваемом сечении конструкции; – вектор-столбец относительных деформаций, являющихся функцией от уровня нагружения и геометрических характеристик сечения S;
– вектор-столбец относительных деформаций, являющихся функцией от уровня нагружения и геометрических характеристик сечения S;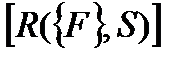 – матрица жесткостей для рассматриваемого сечения, компоненты которой, являются функцией внешних сил, геометрических характеристик сечения и корректируются в зависимости от уровня нагружения;
– матрица жесткостей для рассматриваемого сечения, компоненты которой, являются функцией внешних сил, геометрических характеристик сечения и корректируются в зависимости от уровня нагружения;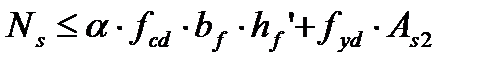 метод предельных усилий
метод предельных усилий - упрощенный деформационный метод.
- упрощенный деформационный метод. - метод предельных усилий,
- метод предельных усилий,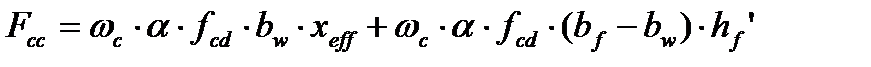 - упрощенный деформационный метод.
- упрощенный деформационный метод.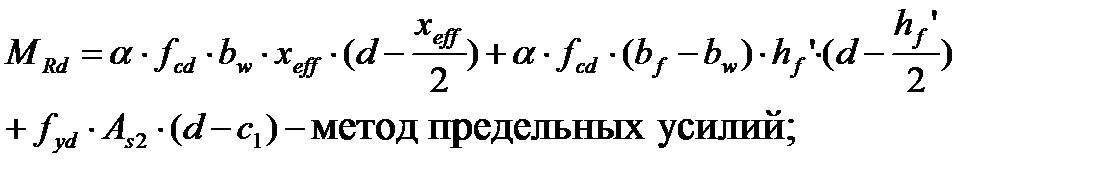
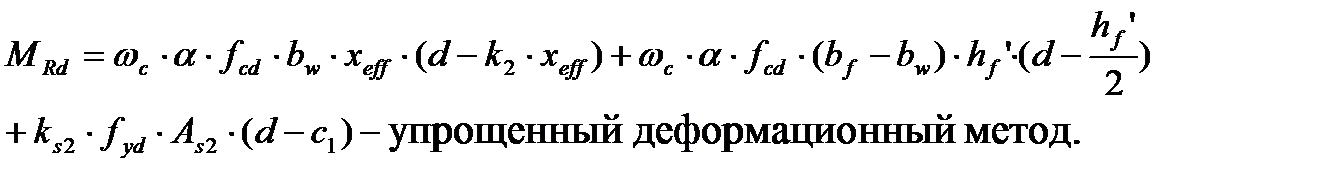 -
-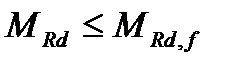 . Если условие соблюдается – граница сжатой зоны пересекает полку, если не соблюдается –ребро.
. Если условие соблюдается – граница сжатой зоны пересекает полку, если не соблюдается –ребро.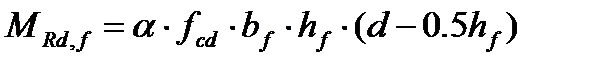 - метод предельных усилий,
- метод предельных усилий, -упрощенный деформационный метод.
-упрощенный деформационный метод.


