
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение поправки компасаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основы астрономического определения поправки компаса Единственным способом определения поправки компаса D К в открытом море является астрономический. Кроме того этот способ обеспечивает наибольшую точность получения D К при условии использования точных координат судна, например при стоянке в порту. D К = ИП св – КП св (98) В отличии от навигационных способов истинный пеленг на светило вычисляется как азимуту светила в круговом счете при решении параллактического треугольника. В зависимости от заданных аргументов в настоящее время используют три метода вычисления азимута на светило (см. разд. 1.2.1.). Метод моментов. В этом методе заданы аргументы jм, dсв и t свм, т. е. А = f (j, d, t) и азимут вычисляется по формуле (4) ctg A =tg cosφ cosec t м – sinφ ctg t м (99) Этот метод универсален – его применяют при любых условиях и он является основой общего способа определения поправки компаса. Метод высот. В этом методе заданы аргументы jм, dсв и h св т. е. А= f (j, d, t) и азимут вычисляется по формуле (5)
(100)
Этот метод применяется в основном в частых случаях, когда известна высота светила, например при восходе (заходе) Солнца. Метод высот и моментов. В этом методе заданы аргументы jм, h св и t свм т. е. А= f (j, h, t) и азимут вычисляется по формуле (6) sin A = sind cos t м sес h (101) Этот метод применяется при одновременном определении места судна (при измерении высот) и поправки компаса, а так же в частном случае при определении D К по Полярной звезде. Постоянная поправка гирокомпаса определяется как средняя по серии отдельных (мгновенных) поправок по формуле
где D ГК i = ИП свi – ГКП свi – мгновенная поправка гирокомпаса; N – число поправок.
Влияние погрешности в счислимых координатах судна на Истинный пеленг светила Так как в формулах (99¸101) в основном используются счислимые координаты судна – jс и lс, то и азимут светила получают счислимый А с, а не истинный А и. Другими словами, погрешности в координатах судна Dj и Dl трансформируются в погрешности в азимуте по широте и долготе, которые можно представить в виде ряда
Продифференцировав формулу (99) по λ и j и выполнив ее преобразование, получим формулу расчета значения поправки D А j D А j = tg h sin A Dj (104) Формула (27) изменения азимута светила в суточном движении получена в разд. 1.3.2. в виде D A t = –(sinφ – tg h cos A cosφ) D t. Так как t м = t гр ± lE W и значение t гр безошибочно (связано только с моментом измерения), то D t = ± DlE W. Другими словами, погрешность в часовом угле светила вызывается погрешностью в счислимой долготе. После замены переменной получим формулу расчета D A l D A l = Для анализа погрешности D А в счислимом азимуте выразим Dj и Dl в формулах (104, 105) через невязку С (снос) и направление невязки С сн и после преобразований получим следующую формулу D А = D А j + D А l = С tg h sin A cos C сн – C (sinj – cosj tg h cos A) sin С сн secj. Основными аргументами влияющих на величину D А являются значения невязки С и высоты светила h. Вычисления по этой формуле при невязке С £ 10 миль и высоте светила h £ 18° дали следующие результаты: в малых широтах D А £ 0,1°; в широтах до 60° D А £ 0,25°; в широтах до 70° ¸ 75° D А £ 0,4°. На основе приведенного анализа получим следующие выводы: · чем меньше высота h, тем меньше погрешность D А; · принимаем ИП сви = ИП свс в широтах до 60° и h £ 18° при С £ 10 миль, а широтах свыше 60° при С £ 3 миль; · в малых северных широтах для определения D К рекомендуется выполнять по Полярной звезде, так как ее азимут практически не изменяется в течении 20м¸30м, т. е. мало зависит от счислимых координат. Частные способы определения поправки компаса Частные способы упрощают получение истинного пеленга на светило. Эти способы применимы только для Солнца в момент видимого восхода (захода) и Полярной звезды. Примечание. Применение общего способа определения D К в этих случаях дает более точный результат особенно для Солнца. Поправка компаса по азимуту видимого восхода (захода) Солнца. Явление видимого восхода (захода) Солнца рассмотрено в разделе 1.6.4.
Высоту центра Солнца в момент видимого восхода (захода) (рис. 53) получим по формуле (54) h = – d – r + p – R , где где d – наклонение видимого горизонта; r – астрономическая рефракция; Азимут видимого восхода (захода) Солнца получим по аргументам j, d и h параллактического D ZP N C 2 по формуле (100) метода высот, полученной в разделе 3.1.1.
По этой формуле вычислены азимуты (в круговом счете), приведенные в ежедневных таблицах МАЕ на каждую дату года. Аргумент высоты Солнца h = –50,3¢ = const. с учетом высоты глаза наблюдателя е = 0 метров (d = 0¢), стандартной астрономической рефракции и параллакса (r + p = –34,3¢), радиуса Солнца (R = –16¢). Аргумент d Солнца вычислен на момент восхода (захода) каждых суток на Гринвичском меридиане. Аргумент широты места задан в виде табличных широт от 74° N до 60° S. Таким образом, получение азимута выполняется по дате и координате широты места судна по формуле А с = А т + D А j + D А l, (106) где D А j – интерполяция по широте места; D А l – интерполяция по долготе места. Действительная высота отличается от табличной (h = –50,3¢) за счет наклонения видимого горизонта d и поправок высоты за температуру и давления атмосферы, которые выбираются из таблиц исправления высот (разд. 2.5.1.), на величину D h д D h д = d + D h t + D h B (107) Дополнительная поправка азимута D А д вычисляется по формуле D А д = –0,0017 tgj D h д cosec A (108) Достоинством этого способа простота и скорость вычисления А с, а так же процесс измерения пеленга не отличается от навигационных измерений. Недостатками являются: · меньшая точность в ГКП за счет только одного измерения; · способ применим два раза в сутки при условии безоблачного неба в районе восхода (захода); · появление больших погрешностей в А с за счет аномального состояния атмосферы в приполярных районах, в которых астрономическая рефракция достигает 1°¸2°. Поправка компаса по Полярной звезде. Движение Полярной звезды происходит по суточной параллелисрадиусом равным полярному расстоянию D» 43¢ (рис. 54).
Вследствие малого сферического радиуса параллели азимут Полярной звезды в широтах до 35°N изменяется всего от 0° до 1° NE и NW. Поэтому для вычисления азимута можно применить формулу (101) метода высот и моментов. Из параллактического D ZCPN получим sin A = sinD sin t м sес h и учитывая, что t м = S м + t и небольшие значения элементов A и D равны их синусам, а так же примем j = h получим расчетную формулу азимута Полярной звезды A = D secj sin(S м +t) (109) По этой формуле, принимая средние значения за год D и t, вычислена таблица в МАЕ «Азимут Полярной» с точностью до 1¢. Аргументами для входа в таблицу являются широта места j и звездное местное время S м. К достоинствами этого способа следует отнести: · простота и скорость обработки наблюдений; · медленное изменение азимута особенно в малых широтах. Азимут практически не изменяется в течении 10 ¸ 20 минут. Недостатком является практическое ограничение применения способа по широте места от 10° N до 35° N. Пеленгование светил. Точность поправки компаса Выполнение пеленгования. Для пеленгования подбирают светила с наименьшей высотой (см. разд. 3.1.2.) в пределах до 35° при прямовидимом пеленговании и наименьшей скорости изменения азимута, т. е. около I-го вертикала (см. выводы изменения азимута в разд. 1.3.2.)
Пеленгование выполняют одновременным совмещением на нити пеленгатора центра светила и пузырька уровня (рис. 55). Снятие ГКП и момента Т производят после нескольких «прицеливаний», пока не получится устойчивый результат или выполняют три измерения ГКП и Т с последующим их осреднением. Процесс одновременного совмещения светила и пузырька уровня требует большой тренировки на ходу судна и особенно при качке. Погрешность компасного пеленга. Погрешность в ГКП складывается из погрешностей гирокомпаса и погрешностей измерения пеленга. Погрешность измерения пеленга возникает в основном от наклона плоскости пеленгования к истинному горизонту (рис. 56).
Положению Z 1 соответствует истинный горизонт S 1 N 1 (пунктирная линия) и вертикал светила Z 1 СП 1. Дуга ZZ 1 равна углу k наклона плоскости пеленгования. Погрешность измерения D А определяется из D CПП 1 по формуле D А = k tg h (110) При удержании пеленгатора в вертикале светила по уровню на ходу судна k» 0,5° и при высотах до 20° погрешность оценивается величиной m КП = ±0,3° [2]. Погрешность гирокомпаса (центральный прибор + репитер) в среднем принимается равной m ГК=0,5° [2]. Погрешность ГКП относительно истинного меридиана m ГКП = 0,6°. Если полученная на ходу судна D К = ±0,5°, то ее принимают равной 0°.
Основы астр ОМС. Задача определения места сводится к определению положения зенита относительно мест светил (ориентиров) на небесной сфере с переходом обратно на поверхность Земли. Примечание. Решение задачи непосредственно на поверхности Земли (геоиде) значительно сложнее по сравнению с решением на сфере. Связь места судна и положением его зенита. Географические координаты j и l точки М и небесные координаты его зенита dz и t z гр связаны соотношениями вытекающими из рис. 57.
По построению (переносу отвесной линии в точке М на Земле в центр О) j = dz. Долгота места l равна дуге небесной сферы QQ ¢, которую можно получить как разность S м – S гр или на основании основной формулы времени как t свм – t свгр, т. е.
l = S м – S гр = t свм – t свгр. Вследствие суточного вращения сферы место зенита непрерывно перемещается по параллели, поэтому по формулам (111) получаем мгновенное место на момент Т гр измерения высоты. Принципы определения места зенита. Для определения мгновенного места зенита (места судна) необходимо иметь данные измерений о его расположении относительно мест двух светил (рис. 58). В навигации, измеряемые физические величины U, являющиеся функциями координат j и l, называются навигационными параметрами [5]. Для светил может быть 8 таких параметров, однако в настоящее время на транспортном флоте применяется только параметр высоты. Весь процесс измерений и их обработки называют астрономической обсервацией. Обработка наблюдений, т. е. определение обсервованного места, может выполняться различными методами [1, 2]. В настоящее время в основном используется графоаналитический метод (метод линий положения см. разд. 3.2.3.). Графический метод, основанный на принципе навигационных изолиний, позволяет пояснить принцип и особенности астрономической обсервации.
На рис. 58 показана обсервация по двум измеренным высотам светил С 1 и С 2, выполненная графическим способом на небесной сфере. Последовательность выполнения решения обсервации по измерениям высот двух светил следующая: · нанести на сферу положение светил С 1 и С 2 по координатам a и d; · проведя изолинии параметров измеренных высот (сферические круги радиусом равным Z i = 90° – h i), получим места двух зенитов; · действительное место зенита наблюдателя (Z м) определяется по дополнительной информации либо по зениту счислимого места (Z сч), нанесенного на сферу (координаты S сч = S гр ± lE W и dz = jсч), либо по измеренному азимуту на любое светило (А 1); · снять координаты точки зенита Z м (S м и dz) и по формулам (111) получить обсервованные географические координаты судна. Кроме рассмотренных методов при решении астрономических задач на компьютере используется итерационный обобщенный метод наименьших квадратов, рассмотренный в курсе «Математические основы судовождения» [5].
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.207 (0.008 с.) |


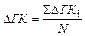 , (102)
, (102) (103)
(103) (sinφ – tg h cos A cosφ) DlE W (105)
(sinφ – tg h cos A cosφ) DlE W (105) Рис. 53
Рис. 53
 Рис. 54
Рис. 54
 Рис. 55
Рис. 55
 Рис. 56
Рис. 56
 Рис. 57
Рис. 57

 Рис. 58
Рис. 58



