
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение места по звездам методом перемещенного местаСодержание книги
Поиск на нашем сайте При обработке наблюдений (решение параллактического треугольника) по иностранным численным таблицам, в которых входными аргументами являются j°мп и t мп°с целыми градусами, применяется метод перемещенного места. В основе метода лежит 3-е свойство ВЛП.– независимость линии положения от счислимых координат. Перемещение счислимых координат делается в пределах ± 30¢. Широту j°мп получают обычным округлением ее до целого градуса. Получение t мп° достигается путем изменения lс для каждой ВЛП на величину Dli. Таким образом, прокладка каждой ВЛП выполняется из своей счислимой точки. Нахождение перемещенных lмпi можно выполнить 3-я приемами. Прием ввода lс + 30¢ Е в расчет t мп° и Dli позволяет избежать ошибок в вычислениях. В этом приеме величина Dli всегда W в пределах от 0¢ до 60¢ откладываются от меридиана lс + 30¢ Е.
Пример. Рассчитать t мп° и Dli, если заданы lс = 30°12,4¢W и t грсв = 323°44,6¢. Для решения параллактического треугольника t мп° = 294°. (Dl W) = 2,2¢ предназначено для нахождения при прокладке на параллели j°мп долготы точки, из которой выполняется прокладка данной ВЛП. Обработка наблюдений производится по вычислительной схеме приведенной в литературе [1], [2]. Оценка обсервации. Вследствие того, что переносы при перемещенном месте могут достигать величины до 40¢, т. е. нарушается 1-е свойство ВЛП, то возникают дополнительные методические ошибки в ВЛП (см. разд. 3.2.5) и оценка места должна выполнятся по формуле
Определение широты по меридиональной высоте светила. Выгодным условием определения широты места (см. разд. 3.2.7.) является нахождение светила в момент кульминации на меридиане наблюдателя. В этом случае высота называется меридиональной (Н) и азимут sin H = sin j sin d + cos j cosd cos 0° или sin H = cos (j – d). Так как Н = 90° – Z, то sin H = cos Z = cos (j – d) и следовательно Z = j – d, откуда j = Z + d.
Наименование Z обратно наименованию Н, которое одноименно с точкой горизонта, над которой измеряется высота. Значение и наименование широты так же зависит от наименования d. Наименования широты и расчетную формулу можно получить при рассмотрении 2-х ситуаций, показанных на рис. 77. 1. Для светила С 1 имеем склонение d1 N и меридиональную высоту Н 1 к S, по которой получим Z 1 N, т. е. Z 1 одноименно со склонением d1. Из рисунка получим формулу расчета широты j = Z 1 + d1 (*) и широта одноименна с Z и d. 2. Для светила С 2 имеем склонение d2 S и меридиональную высоту Н 1 к S, по которой получим ZC 2= Z 2 N, т. е. Z 2 разноименно со склонением d2. Из рисунка получим формулу расчета широты j = Z 2 – d2 (**) и широта одноименна с большим членом формулы По формулам (*) и (**) получим общую формулу расчета широты j = Z ± d. (142) При одноименных Z и d знак «+» и широта одноименна с ними. При разноименных Z и d знак «–» и широта одноименна с большим членом (Z или d) формулы. Рекомендуется получить решение задачи на сфере как на рис. 77. Последовательность решения: 1. Изобразить меридиан наблюдателя, отвесную линию и горизонт. Обозначить точки N и S горизонта. 2. По высоте Н нанести положение светила и наименования точек горизонта. 3. Отложив от светила d, получим положение экватора, а затем перпендикулярно ему провести ось мира. 4. По рисунку составить формулу расчета широты. Обычно метод определения широты по Н применяется только для Солнца. Время начала наблюдений определяется как Т снаб = Т ск – 5м. Измерение меридиональной высоты выполняется приведением нижнего края отраженного Солнца к касанию с горизонтом с помощью барабана отсчетного устройства до момента уменьшения высоты Солнца. Пример полной обработки наблюдений для определения jо приведен в литературе [1]. Здесь приведем только вычислительную схему обработки наблюдений. Расчет кульминации Расчет склонения Расчет широты
Достоинством определение широты места по меридиональной высоте Солнца является не зависимость метода от счислимой широты места (не требуется знания j места), а также скорость получения результата. Определение широты по высоте Полярной звезды. Метод получения обсервованной широты места основан на переходе от обсервованной высоты Полярной звезды к широте путем введения 3-х поправок.
Полярная звезда (a Малой Медведицы) находится вблизи северного полюса мира. Полярное расстояние для нее на 2005 г. D = 43¢ N. Поэтому она всегда находится в выгодных условиях для определения широты (см. разд. 3.2.7.). В своем суточном движении она описывает параллель аа ¢ (рис. 78) и как видно из рисунка высота отличается от широты на величину х, причем в точке а параллели х = –D; в точке а ¢ х = +D. Из рис. 78 видно, что для любой точки параллели широта определяется формулой j = h ± х. (143
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 lс + 30¢ Е
lс + 30¢ Е
 (141)
(141) Рис. 77
Рис. 77
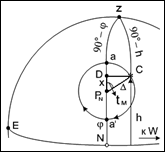 Рис. 78
Рис. 78



