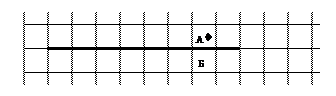Величины и их характеристики

 

При решении многих задач надо уметь запоминать, изменять и использовать информацию в памяти компьютера (например, в рассмотренной задаче это информация об опасном уровне радиации и числе сделанных вправо шагов). Для этого в алгоритмическом языке используются величины.

Термин «величина» заимствован из математики и физики, поскольку в алгоритмах для решения математических или физических задач величины алгоритмического языка соответствуют математическим или физическим величинам.

Каждая величина имеет имя, тип, вид и значение.

Имя величины служит для обозначения величины в алгоритме. Именем величины в алгоритмическом языке может быть любое слово (кроме служебных слов самого языка) или даже несколько слов. В имя могут входить русские и латинские буквы и даже цифры (правда, начинаться с цифры имена не могут), а также пробелы и знаки подчеркивания. Вот несколько примеров допустимых имен:.s, R, слово 1, длинное имя.

Тип величины показывает, какие значения может принимать величина и какие операции можно с ней выполнять. Пока мы будем пользоваться двумя типами: вещественным (вещ) и целым (цел). Значением величины вещественного типа может быть любое число, а целого — только целое. Необходимость различать эти типы связана с тем, что они по-разному обрабатываются компьютером: все вычисления с целыми числами выполняются точно, а с вещественными — приближенно (хотя и с высокой точностью). Позже мы познакомимся с величинами некоторых других типов.

Вид величины показывает ее информационную роль в алгоритме. Аргументы содержат исходную информацию, необходимую для работы алгоритма, а промежуточные величины предназначены для хранения текущей информации, которую обрабатывает алгоритм. Позднее мы познакомимся с другими видами величин.

Во время выполнения алгоритма в каждый конкретный момент величина имеет какое-то значение (например, 22 или -107) либо не определена.

Имя, тип и вид величины можно однозначно определить по тексту алгоритма. Это статические характеристики величины. Значение определяется только во время выполнения. Это динамическая характеристика.

 

Описание величин

 

Чтобы компьютер мог работать с величиной, нужно указать ее вид, тип и имя. Такое указание называется описанием величины.

Аргументы описывают в заголовке алгоритма, явно указывая вид, тип и имя, например аргвещ у.

Промежуточные величины описывают в теле алгоритма после слова нач. Их вид специально никак не обозначается, так как именно описание в теле алгоритма говорит о том, что это промежуточная величина.

 

Модель памяти компьютера

 

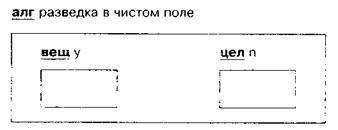
Для запоминания информации в компьютере имеется память. Напомним, что память компьютера удобно представлять в виде классной доски, на которой можно записывать информацию, читать, стирать, записывать заново и т. д. Место, отводимое в памяти компьютера для каждой величины, удобно изображать в виде прямоугольника. Значение величины (если она определена) записывается внутри прямоугольника, а тип и имя указываются сверху:

Если величина не определена, то в прямоугольнике ничего не пишется.

Рассмотрим работу памяти на примере алгоритма А52.

В начале выполнения алгоритма компьютер выделит для него часть памяти:

Встретив после слова нач описания вещ у и цел n, компьютер отведет внутри памяти алгоритма место для хранения двух величин: первая имеет вещественный тип и имя у, вторая — целый тип и имя п.

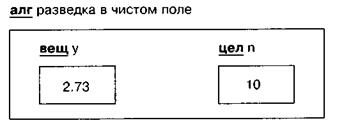
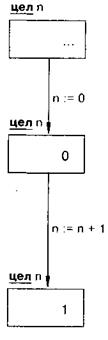
После первых двух команд алгоритма эти величины получат значения. В ячейке п будет 0, а в ячейке у — значение радиации в клетке с Роботом.

При дальнейшем исполнении алгоритма значение величины у уже не изменится, а п будет увеличиваться по мере продвижения Робота в тупик. В конце выполнения алгоритма память может выглядеть так:

Когда выполнение алгоритма заканчивается, память освобождается, значения промежуточных величин пропадают.

 

Команда присваивания

 

Для запоминания или изменения значения величины в алгоритмическом языке есть специальная команда — команда присваивания, которая записывается в виде:

 

имя величины:= выражение

 

Знак «:=» (двоеточие, а потом равенство) называется знаком присваивания и читается как «присвоить» (например, команда n:= е читается: «п присвоить е»). При выполнении команды присваивания компьютер сначала вычисляет записанное в правой части выражение (заменяя имена величин на их значения), а потом полученное значение выражения записывает в память.

 

Примеры использования команды присваивания

 

 

16.9. Еще один пример алгоритма, работающего с величинами

 

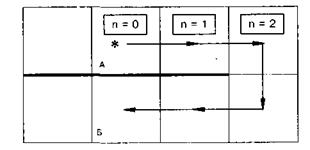
Рассмотрим следующую задачу. Робот расположен в клетке над горизонтальной стеной неизвестной длины. Надо переместить Робота на клетку вниз — «сквозь стену» (рис. 57).

 

Рис. 57

 

Поскольку Робот сквозь стену проходить не умеет, стену нужно обойти. Сделать это можно так. Пока ниже Робота стена, будем двигать его вправо и по дороге считать число шагов (число команд вправо). Как только стена кончится, сместим Робота вниз и начнем двигать его обратно (влево). Тут нам и понадобится запомненная ранее информация о числе шагов вправо: скомандуем Роботу влево столько же раз, сколько было сделано шагов вправо, и он окажется в точке Б.

Запишем теперь алгоритм "вниз сквозь стену", используя для подсчета сделанных вправо шагов целочисленную величину п:

	А53

алг вниз сквозь стену

дано | Робот над горизонтальной стеной, других стен нет

надо | Робот под стеной, на клетку ниже исходного положения

нач цел n

n:=0

нц пока снизу стена

I вправо; n:= n + 1

кц

вниз

влево

кц

Кон

При выполнении этого алгоритма компьютер сначала присвоит величине п значение 0 (команда n:= 0). Затем в цикле компьютер будет командовать Роботу вправо и тут же увеличивать значение п на 1 (команда n:= n + 1). После каждого выполнения тела цикла значение п окажется равным числу сделанных Роботом шагов вправо. После окончания цикла значением п будет общее число сделанных вправо шагов. Поэтому, при выполнении нц n раз компьютер п раз скомандует влево, Робот окажется в точности на клетку ниже исходного положения (рис. 58).

Рис. 58

 

Рисование параболы

 

Рассмотрим следующую задачу: изобразить с помощью Чертежника график функции (параболу) у = х². Условие этой задачи нуждается в уточнении. Во-первых, нарисовать весь график нельзя — ведь он бесконечен. Поэтому будем рисовать только его часть, например от х = 0 до х = 2. Во-вторых, Чертежник не умеет рисовать ничего, кроме отрезков, а график функции у = х² — это кривая. Поэтому параболу придется заменить ломаной. Если вершины ломаной лежат на параболе и звенья ломаной очень короткие, то ломаная на вид почти не отличается от параболы. На рисунке 59, а ломаная имеет 4 звена, на рисунке 59, б — 10 звеньев, на рисунке 75, в — 100 звеньев.

Рис. 59

 

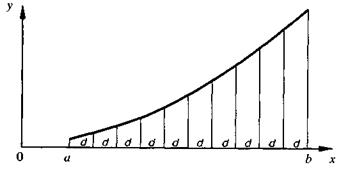
В общем случае с помощью Чертежника можно изобразить параболу на некотором участке (от а до b) в виде ломаной из какого-то числа звеньев (п).

Будем рисовать ломаную слева направо, начиная от точки (а,а**2) и кончая точкой (b,b**2). От вершины к вершине будем перемещаться с помощью команды Чертежника сместиться в точку.

Используем вещественную величину х для запоминания x-координаты очередной вершины ломаной.

Разобьем отрезок от а до b на п равных частей длины d = (b -а)/п (рис. 60).

При рисовании очередного звена ломаной величину х надо просто увеличивать на d — это можно сделать с помощью команды присваивания

х:= х + d:

	А54

алг парабола (арг вещ а, b, арг цел n)

дано n > 0 | перо Чертежника поднято

надо | нарисован график функции у = х**2 на участке от а до b

| в виде ломаной из n звеньев; перо в точке (b, b**2) и поднято

нач вещ х, d

х:= а; d:= (b - а)/n

сместиться в точку (а, а**2)

опустить перо

нц n раз

х:= х + d

сместиться в точку(х, х**2)

кц

поднять перо

Кон

При выполнении вызова "парабола (0, 2, 10)" компьютер выдаст Чертежнику последовательно 13 команд:

сместиться в точку (0, 0)

опустить перо

сместиться в точку (0.2, 0.04)

сместиться в точку (0.4, 0.16)

сместиться в точку (0.6, 0.36)

сместиться в точку (0.8, 0.64)

сместиться в точку (1.0, 1.00)

сместиться в точку (1.2, 1.44)

сместиться в точку (1.4, 1.96)

сместиться в точку (1.6, 2.56)

сместиться в точку (1.8, 3.24)

сместиться в точку (2.0, 4.00)

поднять перо

и Чертежник нарисует параболу на участке от 0 до 2 в виде ломаной из 10 звеньев.

Рис.60.

 

ЗАДАЧИ И УПРАЖНЕНИЯ

1. Значение величины х равно 3. Чему оно будет равно после выполнения команды:

а) х:= 5; б) х:= х + 5; в) у:= х?

 

2... После выполнения команды

а) х:= х+5; б) х:=-х; в) у:= х

 

или серии команд

 

г) у:= 1; х:= х + у; д) у:= х; х:= у

 

значение величины х стало равно 3. Чему было равно значение величины х до выполнения в каждом из этих случаев?

 

3. После выполнения команды присваивания х:= х + у значение величины х равно 3, а значение у равно 5. Чему были равны значения величин х и у до выполнения команды?

 

4. Значение величины х равно а, значение у равно b. После выполнения каких из указанных ниже последовательностей команд значения величин х и у поменяются, т. е. х станет равно b, а у станет равно а?

а) х:= у б) t:=х в) х:= х + у г) t:= х

y:= х х:= у у:= х - у у:= t

у:= t х:= х - у х:= у

 

5. Опишите, что произойдет при выполнении алгоритма "вниз сквозь стену" для начальных положений Робота, указанных на рисунке 61.

 

Рис. 61

 

 

6. Дан алгоритм:

 

А55

алг график (арг вещ b, арг цел n)

дано n > 0 I перо Чертежника поднято

надо | нарисован график некоторой функции на участке от 0

| до b в виде ломаной из n звеньев; перо в конце графика и поднято

нач вещ х,d, v

х:= 0; b := b /n

сместиться в точку (0, 0)

опустить перо

нц n раз

v:= 2*х*d + d*d; х:= х + d

сместиться на вектор (d, v)

кц

поднять перо

Кон

а) Как будет выглядеть память ЭВМ при выполнении вызова "график(2, 10)"?

б) Что нарисует Чертежник при выполнении этого вызова?

 

7. Робот находится перед входом в тупик, идущий вправо. Составьте алгоритм, при выполнении которого с помощью Чертежника будет нарисован график радиоактивности в тупике (считая, что единица масштаба по оси Ох равна размеру клетки на поле Робота).

 

8. Составьте алгоритмы со следующими заголовками:

а) алг вниз до стены закрасить и вернуться

дано | где-то ниже Робота есть стена

надо | Робот дошел до этой стены, закрасил клетку

| и вернулся в исходное положение

 

б) алг закрасить клетку в правом нижнем углу

дано |Робот где-то внутри прямоугольника, огороженного стенами, других стен нет

надо |Робот закрасил клетку в правом нижнем углу

|прямоугольника и вернулся в исходное положение

 

в) алг отойти вдвое дальше от левой стены

дано |где-то левее Робота есть стена, других стен нет

надо | Робот отошел вправо на расстояние от стены вдвое большее, чем исходное

 

г) алг симметрия

дано |где-то ниже Робота есть горизонтальная стена длиной в одну клетку, других стен нет

надо |Робот оказался в положении, симметричном исходному относительно стены

 

д) алг симметрия

дано |где-то ниже Робота есть горизонтальная стена,

|которая и вправо и влево кончается, других стен нет

надо |Робот оказался в положении, симметричном исходному относительно стены

 

е) алг обойти прямоугольное препятствие

дано | Робот над прямоугольником, огороженным стенами, других стен нет

надо | Робот под прямоугольником на той же вертикали

 

ж) алг вниз сквозь бесконечную стену

дано |Робот над горизонтальной стеной, в одну сторону

|уходящей в бесконечность, других стен нет

надо |Робот под стеной на клетку ниже исходного положения

 

9. Робот находится в левом верхнем углу прямоугольника, огороженного стенами. Составьте алгоритм, после выполнения которого, Робот будет стоять в клетке с минимальным уровнем радиации.

Алгоритмы с результатами

17.1. Простейший пример алгоритма с результатами

Как мы уже знаем, для задания исходной информации в алгоритме используются аргументы. Но алгоритм может не только получать информацию, но и отдавать ее (рис. 62). Для этого существует специальный вид величины — результаты.

 

Рис. 62

 

Рассмотрим пример алгоритма с результатом.

	А56

алг гипотенуза (арг вещ а, b, рез вещ с)

дано а >= 0 и b >= 0 | длины катетов треугольника

надо | с = длина гипотенузы этого треугольника

Нач

| с:= sqrt (а**2 + b**2)

Кон

Запись рез вещ с означает, что результат (рез) выполнения этого алгоритма — одна вещественная (вещ) величина, которая в алгоритме обозначена как с.