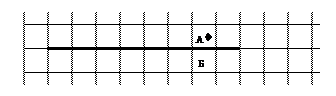Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности записи чисел в информатикеСодержание книги
Поиск на нашем сайте
Особенности записи чисел в информатике В информатике для отделения целой части числа от дробной используется точка, а не запятая, как в школьной математике (например, 1.7 или 2.5). Это позволяет записывать несколько рядом стоящих чисел через запятую без риска вызвать путаницу (например, 1.7, 2.5, -11.3, 2, 3.14). При задании точек плоскости координаты х и у в информатике разделяются запятой (рис. 37).
Рис. 37
13.2. Исполнитель Чертежник Чертежник предназначен для построения рисунков, чертежей, графиков и т. д. на бесконечном листе бумаги. Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след — отрезок от старого положения пера до нового. Всего Чертежник умеет выполнять четыре команды: опустить перо поднять перо сместиться в точку (арг вещ х, у) сместиться на вектор (арг вещ а, b) По команде опустить перо Чертежник опускает перо. Если перо уже было опущено, Чертежник не выполняет никаких действий, но и отказа не происходит. Таким образом, после выполнения команды опустить перо перо оказывается опущенным (готовым к рисованию) независимо от его предыдущего положения. Аналогично по команде поднять перо перо будет поднято. Выполнение этой команды тоже не может привести к отказу. Команды сместиться в точку и сместиться на вектор перемещают перо Чертежника. Если при этом перо опущено, на бумаге остается след. Таким образом, эти команды позволяют строить чертежи и рисунки. Команды с параметрами В отличие от Робота, который всегда двигался ровно на одну клетку, смещение Чертежника может быть произвольным. Поэтому для выполнения команд сместиться в точку и сместиться на вектор необходимо задать дополнительную информацию — указать, куда надо переместить перо Чертежника. Эта дополнительная информация записывается в команде в виде аргументов — вещественных (действительных) чисел, которые помещаются в скобках после имени команды. Например: сместиться в точку (2, 3) или сместиться на вектор (1.4, 2.3). Необходимость аргументов указывается в описании команды: сместиться в точку (арг вещ х, у) сместиться на вектор (арг вещ а, b) Подробнее смысл слов арг и вещ раскрывается в § 14.
Нач
опустить перо сместиться в точку (3, 1) сместиться в точку (3, 2) сместиться в точку (1,2) сместиться в точку (1,1) утв | нарисован прямоугольник сместиться в точку (3, 2) поднять перо сместиться в точку (1, 2) опустить перо сместиться в точку (3, 1) поднять перо Кон Рисование букв С помощью Чертежника можно рисовать любые фигуры, построенные из отрезков, например буквы. Составим алгоритм, при выполнении которого Чертежник рисует на клетчатой бумаге букву М (рис. 40; размеры каждой клетки 1x1). Поскольку начальное положение пера на плоскости не задано, то придется воспользоваться командой сместиться на вектор:
алг буква М дано | перо в точке А (рис. 40) и поднято надо | нарисована буква М (рис. 40), перо в точке Б и поднято Нач
сместиться на вектор (0, 4) сместиться на вектор (1, -2) сместиться на вектор (1,2) сместиться на вектор (0, -4) поднять перо сместиться на вектор (1,0) кон
Рис. 40 Рис. 41
Аналогично можно составить алгоритмы "буква И", "буква Р" и "буква У" (рис. 40). Нач
сместиться на вектор (4, 0) сместиться на вектор (0, 4) сместиться на вектор (-4, 0) сместиться на вектор (0, -4) поднять перо сместиться на вектор (0, 4) опустить перо сместиться на вектор (2, 2) сместиться на вектор (2, -2) поднять перо сместиться на вектор (-4, -4) Кон 3. Измените алгоритм "домик" (А34) так, чтобы домик рисовался с окошком.
алг улица из трех домиков Нач
домик; сместиться на вектор (6, 0) домик Кон Этот алгоритм использует вспомогательный алгоритм "домик" (А34). Нарисуйте результат выполнения алгоритма А35 (полученную картинку и положение пера Чертежника). 5. Составьте алгоритм рисования улицы из шести домиков. 6. Петя зачеркнул последнюю команду сместиться на вектор (-4, -4) в алгоритме "домик" (А34). Как Коля должен изменить алгоритм "улица из трех домиков" (А35), чтобы рисовалась та же картинка, что и раньше? 7. Составьте алгоритм управления Чертежником, после выполнения, которого будут нарисованы: а) отрезок с концами в точках (1, 2) и (-1, 1); б) квадрат со сторонами длины 4, параллельными координатным осям, так, чтобы левый нижний угол квадрата совпадал с начальным положением пера Чертежника;
в) квадрат со сторонами длины 6, параллельными координатным осям, так, чтобы левый нижний угол квадрата совпадал с начальным положением пера Чертежника; г) какой-нибудь отрезок длины 3, проходящий через точку (2, 2); д) какой-нибудь квадрат со сторонами длины 2 и центром в начале координат; е) какой-нибудь прямоугольник с длинами сторон 3 и 4, содержащий внутри себя начало координат; ж) какой-нибудь параллелограмм. 8. Составьте алгоритм управления Чертежником, после исполнения, которого будут нарисованы: а) инициалы полководца Кутузова; б) ваши инициалы; в) буква «Ф»; г) зеркальные отражения букв «И» и «Р» относительно горизонтальной оси; д) число 12 римскими цифрами; е) слово «МГУ»; ж) почтовый индекс 161110 (цифры индекса должны быть написаны как на почтовых конвертах). 9. Составьте алгоритм для рисования фигур, изображенных на рисунке 42, так, чтобы в процессе рисования перо не отрывалось от бумаги и ни одна линия не проводилась дважды
Рис. 42 14 Составьте десять алгоритмов для изображения десяти цифр почтового индекса так, чтобы при их последовательном вызове цифры рисовались друг за другом. Используя эти алгоритмы как вспомогательные, напишите ваш почтовый индекс. 14 По образцу алгоритма "МИР" (А33) составьте алгоритмы: а) РИМ; б) МИМ. 14 Измените алгоритмы рисования букв «М», «И», «Р» так, чтобы при последовательном вызове этих алгоритмов слово «МИР» оказалось написанным: а) с удвоенным расстоянием между буквами; б) буквами удвоенного размера; в) сверху вниз; г) сверху вниз буквами удвоенного размера.
алг фигура дано | перо в начале координат и поднято Нач
опустить перо сместиться на вектор (0, 3) сместиться на вектор (1,0) сместиться на вектор (0, -1) сместиться на вектор (1,0) сместиться на вектор (0, -1) сместиться на вектор (1,0) сместиться на вектор (0, -1) сместиться в точку (2, 1) поднять перо Кон а) не выполняя алгоритма и не рисуя получившейся фигуры, определите, где будет расположено перо после выполнения алгоритма, будет ли оно поднято или опущено; б) выполните алгоритм, нарисуйте получившуюся фигуру; в) переделайте алгоритм так, чтобы он рисовал где-нибудь на плоскости фигуру вдвое большего размера; г) переделайте алгоритм так, чтобы он рисовал фигуру, симметричную первой относительно оси у; д) определите, что будет нарисовано, если в алгоритме изменить знаки всех аргументов на противоположные
12. Дан алгоритм:
дано | перо в начале координат и поднято Нач
сместиться на вектор (1, 3) сместиться на вектор (1, 2) сместиться на вектор (1, 1) сместиться на вектор (1, 0) сместиться на вектор (1, -1) сместиться на вектор (1, -2) сместиться на вектор (1, -3) поднять перо Кон Не выполняя алгоритма и не рисуя получившейся ломаной, определите: а) будет перо после выполнения поднято или опущено; б) координату х конечного положения пера; в) координату у конечного положения пера; г) будет ли ломаная замкнута; д) расстояние между концами ломаной. Нарисуйте ломаную, проверьте ваши ответы. 15. Составьте алгоритм управления Чертежником, после исполнения, которого будет нарисован квадрат 4x4, заштрихованный горизонтальными и (или) вертикальными линиями на рисунке 43 (расстояние между линиями равно 0,4).
Рис. 43
Алгоритмы с аргументами Пример алгоритма с аргументом
Вспомните упражнения 7, б), в) из предыдущего параграфа. Для рисования квадратов с длинами сторон 4 и 6 вы составляли два разных алгоритма, отличающихся только числами в командах. А как быть, если нужно рисовать много разных квадратов с разными длинами сторон? Можно, конечно, составить множество похожих алгоритмов, но делать этого очень не хочется! Было бы намного удобнее создать единый алгоритм-образец, в который компьютер сам подставлял бы каждый раз нужные числа. Для подобных целей в алгоритмическом языке существуют алгоритмы с аргументами. Например, алгоритм рисования квадрата с произвольной длиной стороны может выглядеть так:
алг квадрат (арг вещ а) дано | перо Чертежника в левом нижнем углу будущего | квадрата и поднято надо | нарисован квадрат с длиной стороны а, перо Чертежника | в исходной точке и поднято Нач
сместиться на вектор (а, 0) сместиться на вектор (0, а) сместиться на вектор (-а, 0) сместиться на вектор (0, -а) поднять перо кон Запись " алг квадрат (арг вещ а)" означает, что у алгоритма "квадрат" есть один аргумент (арг) а, который может быть произвольным числом. Слово вещ — это сокращение от «вещественный», этим словом в информатике принято обозначать числа, которые могут быть целыми или дробными (в математике такие числа называют действительными). Это слово описывает тип аргумента. Тип указывает, какие значения может принимать величина и какие действия можно с ней выполнять. Позже мы познакомимся с алгоритмами, аргументы которых могут быть лишь целыми (цел) числами; с алгоритмами, аргументы которых вообще не являются числами; а также с алгоритмами, у которых, кроме аргументов, есть результаты (рез). Именно этим объясняется необходимость слов арг и вещ в заголовке алгоритма "квадрат".
Модель памяти компьютера
Поясним подробнее, как компьютер запоминает значения аргументов в своей памяти. Память компьютера удобно представлять в виде обычной классной доски, на которой можно записывать информацию, читать, стирать, записывать заново и т. д. Место, отводимое в памяти компьютера для хранения информации, удобно изображать прямоугольником, внутри которого записывается сама информация (значение аргумента). Такой прямоугольник мы будем называть ячейкой памяти.
При выполнении каждого алгоритма ему выделяется отдельный участок памяти, где создаются ячейки для аргументов. После окончания выполнения алгоритма эта память освобождается. Память алгоритма удобно изображать в виде большого прямоугольника, внутри которого находятся прямоугольники меньшего размера, соответствующие ячейкам.
Возможный вид памяти при исполнении алгоритма "квадрат" показан на рисунке 44 (здесь а=4)
Рис. 44
Нач
сместиться на вектор (а, 0) сместиться на вектор (0, b) сместиться на вектор (-а, 0) сместиться на вектор (0, - b) поднять перо Кон
При вызове такого алгоритма важно правильно задать порядок следования аргументов. Соответствие между аргументами в команде вызова и в заголовке алгоритма устанавливается по порядку их следования. На рисунке 45, а показано изображение, полученное при вызове "прямоугольник (3, 7)", а на рисунке 45, б — изображение, полученное при вызове "прямоугольник (7, 3)". Рис. 45
14.5. Аргументы в заголовке цикла n раз
Аргументы алгоритма можно использовать в любых командах алгоритмического языка, где могут быть числа, в том числе в заголовке цикла n раз. При помощи цикла n раз с аргументом можно составить алгоритмы для смещения Робота на заданное число клеток в нужном направлении, например:
дано | на поле Робота стен нет надо | Робот сместился на n клеток влево нач
| влево Кц Кон Аналогично можно составить алгоритмы "вниз на (арг цел n)", "вверх на (арг цел n)" и "вправо на (арг цел n)". В дальнейшем мы часто будем пользоваться этими алгоритмами как вспомогательными. Обратите внимание, что без помощи цикла n раз алгоритм А40 составить нельзя. Таким образом, применение аргументов открывает новые возможности в использовании этой простой конструкции: цикл n раз с аргументом не только сокращает запись, но и позволяет решать задачи, для которых невозможен простой линейный алгоритм.
Закрашивание прямоугольника
В § 9 мы решали задачу о закрашивании Роботом прямоугольника. Тогда мы вынуждены были указывать в алгоритме конкретные размеры прямоугольника. Используя аргументы, мы можем переписать этот алгоритм так, чтобы при его выполнении закрашивался прямоугольник произвольного размера.
дано | на поле Робота стен нет надо | закрашен прямоугольник размером m*n, Робот в исходном положении
закрасить ряд (m) вниз кц вверх на (n) Кон
алг закрасить ряд (арг цел m) дано | на поле Робота стен нет надо | Робот закрасил m клеток вправо и вернулся в исходное положение нач
|закрасить; вправо кц
| влево Кц Кон
алг вверх на (аргцел n)
надо | Робот сместился на n клеток вверх нач
| вверх Кц Кон
Нач квадрат (10); сместиться на вектор (1,1) квадрат (7); сместиться на вектор (1,1)
квадрат (4); сместиться на вектор (1,1) квадрат (1) Кон
Нач опустить перо виток (1); виток (3); виток (5); виток (7); виток (9) поднять перо Кон
Нач сместиться на вектор (а, 0) сместиться на вектор (0, -а) сместиться на вектор (-а -1,0) сместиться на вектор (0, а + 1) Кон Что нарисует Чертежник при выполнении алгоритма "спираль" (А45), если в алгоритме "виток" (А46) всюду заменить 1 на 2?
Составьте алгоритм рисования спирали, изображенной на рисунке 50. Измените ваше решение упражнения 11 так, чтобы расстояние между витками при каждом новом витке увеличивалось.
Рис. 50
13. Нарисуйте результат выполнения алгоритма "орнамент":
дано | перо Чертежника в левом верхнем углу будущего | орнамента размером 12x12 и поднято надо | нарисован орнамент, перо в левом нижнем углу и поднято Нач | ряд; ряд; ряд Кон
дано | перо Чертежника в левом верхнем углу будущего ряда | размером 12x4 и поднято надо | нарисован ряд, перо в левом нижнем углу ряда и поднято Нач I фрагмент; фрагмент; фрагмент I сместиться на вектор (-12,-4) Кон
дано | перо Чертежника в левом верхнем углу будущего | фрагмента размером 4x4 и поднято надо | нарисован фрагмент, перо в правом верхнем углу и поднято Нач опустить перо сместиться на вектор (2, -2) сместиться на вектор (-2, -2) поднять перо; сместиться на вектор (4, 0); опустить перо сместиться на вектор (0, 1) сместиться на вектор (-2, 0) сместиться на вектор (0, 2) сместиться на вектор (2, 0) сместиться на вектор (0, 1) поднять перо Кон
Рис 51
13. По образцу упражнения 13 составьте алгоритмы рисования орнаментов (рис. 51).
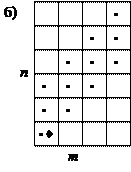
15. Составьте алгоритм "горизонтальная ломаная (аргцел n, аргвещ а)", рисующий с помощью Чертежника ломаную линию с 2 n звеньями, показанную на рисунке 52.
Рис. 52
16. Составьте алгоритм "вертикальная ломаная (аргцел n, арг вещ а)", рисующий ломаную из упражнения 15, повернутую вокруг начального положения пера на 90° по часовой стрелке. 17. Используя алгоритмы из упражнений 15 и 16 как вспомогательные, составьте алгоритмы, рисующие: а) т горизонтальных ломаных с 2 n звеньями одна под другой на расстоянии b друг от друга; б) т вертикальных ломаных с 2 n звеньями одна под другой на расстоянии b друг от друга. 18. Компьютер выполнил последовательность команд: горизонтальная ломаная (5, 1) вертикальная ломаная (7, 1) горизонтальная ломаная (5,-1) вертикальная ломаная (7, -1) Что нарисовал Чертежник? 19. Составьте алгоритм с целыми аргументами m и n, который с помощью Робота закрашивает клетки, отмеченные на рисунке 53.
Рис. 53
Нач
сместиться на вектор (0, в) сместиться на вектор (а/2, -в/2) сместиться на вектор (а/2, в/2) сместиться на вектор (0, -в) поднять перо сместиться на вектор (а/2, 0) Кон Знак «/» здесь означает деление. Таким образом, запись «а/2» означает «(а + в)/с» означает
Нач нц пока справа свободно вправо если радиация > а то закрасить Все кц нц пока сверху стена влево Кц Кон
Все кц нц пока сверху стена влево Кц Кон Для организации работы с памятью компьютера в алгоритмическом языке используются величины. В алгоритме А51 использована одна величина у. Выделение ячейки памяти для хранения информации происходит при описании величины (вещ у), а занесение в ячейку нужной информации происходит при выполнении команды присваивания (у:=радиация). Подробнее о работе с величинами рассказано в разделах 16.4 — 16.8.
Компьютер выполняет подсчет
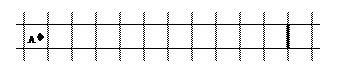
Еще усложним условие задачи. Пусть опасные клетки надо отметить не в тупике, а на участке свободного пространства между Роботом и стеной (рис. 56). Изменение ситуации не мешает выполнить разметку уже известным способом, но при возвращении в исходное положение возникает проблема: как узнать, в какой клетке остановиться?
Рис. 56
При непосредственном управлении Роботом мы можем считать шаги, которые он делает при движении к стене. Когда Робот подойдет к стене, мы будем знать пройденное им расстояние и сможем приказать ему сделать такое же число шагов в обратную сторону. При программном управлении необходимо, чтобы считать шаги мог компьютер. Как это делается, показано в алгоритме:
дано | где-то справа от Робота есть стена надо | закрашены все клетки между Роботом и стеной, | в которых уровень радиации выше, чем в исходном | положении Робота | Робот в исходном положении нач вещ у | создать ячейку с именем у цел n | создать ячейку n для подсчета количества шагов у:= радиация | запомнить значение радиации n:= 0 | обнулить счетчик нц пока справа свободно вправо n:= n + 1 | увеличить на 1 счетчик количества шагов если радиация > у то закрасить Все кц нц n раз влево кц Кон В этом алгоритме использованы две величины. Величина у используется для хранения «опасного» уровня радиации. Этот уровень запоминается в исходном положении Робота и в дальнейшем многократно используется. Величина п играет роль счетчика. В начальный момент счетчик «обнуляется» командой n:=0, а затем многократно увеличивается командой n:=n+1.
Описание величин
Чтобы компьютер мог работать с величиной, нужно указать ее вид, тип и имя. Такое указание называется описанием величины. Аргументы описывают в заголовке алгоритма, явно указывая вид, тип и имя, например аргвещ у. Промежуточные величины описывают в теле алгоритма после слова нач. Их вид специально никак не обозначается, так как именно описание в теле алгоритма говорит о том, что это промежуточная величина.
Модель памяти компьютера
Для запоминания информации в компьютере имеется память. Напомним, что память компьютера удобно представлять в виде классной доски, на которой можно записывать информацию, читать, стирать, записывать заново и т. д. Место, отводимое в памяти компьютера для каждой величины, удобно изображать в виде прямоугольника. Значение величины (если она определена) записывается внутри прямоугольника, а тип и имя указываются сверху:
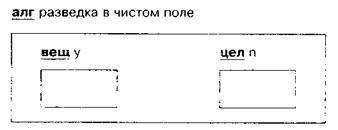
Если величина не определена, то в прямоугольнике ничего не пишется. Рассмотрим работу памяти на примере алгоритма А52. В начале выполнения алгоритма компьютер выделит для него часть памяти:
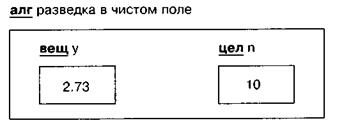
Встретив после слова нач описания вещ у и цел n, компьютер отведет внутри памяти алгоритма место для хранения двух величин: первая имеет вещественный тип и имя у, вторая — целый тип и имя п.
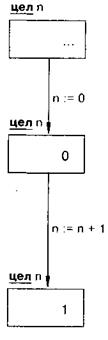
После первых двух команд алгоритма эти величины получат значения. В ячейке п будет 0, а в ячейке у — значение радиации в клетке с Роботом.
При дальнейшем исполнении алгоритма значение величины у уже не изменится, а п будет увеличиваться по мере продвижения Робота в тупик. В конце выполнения алгоритма память может выглядеть так:
Когда выполнение алгоритма заканчивается, память освобождается, значения промежуточных величин пропадают.
Команда присваивания
Для запоминания или изменения значения величины в алгоритмическом языке есть специальная команда — команда присваивания, которая записывается в виде:
имя величины:= выражение
Знак «:=» (двоеточие, а потом равенство) называется знаком присваивания и читается как «присвоить» (например, команда n:= е читается: «п присвоить е»). При выполнении команды присваивания компьютер сначала вычисляет записанное в правой части выражение (заменяя имена величин на их значения), а потом полученное значение выражения записывает в память.
Примеры использования команды присваивания
16.9. Еще один пример алгоритма, работающего с величинами
Рассмотрим следующую задачу. Робот расположен в клетке над горизонтальной стеной неизвестной длины. Надо переместить Робота на клетку вниз — «сквозь стену» (рис. 57).
Рис. 57
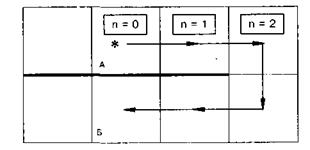
Поскольку Робот сквозь стену проходить не умеет, стену нужно обойти. Сделать это можно так. Пока ниже Робота стена, будем двигать его вправо и по дороге считать число шагов (число команд вправо). Как только стена кончится, сместим Робота вниз и начнем двигать его обратно (влево). Тут нам и понадобится запомненная ранее информация о числе шагов вправо: скомандуем Роботу влево столько же раз, сколько было сделано шагов вправо, и он окажется в точке Б. Запишем теперь алгоритм "вниз сквозь стену", используя для подсчета сделанных вправо шагов целочисленную величину п:
алг вниз сквозь стену дано | Робот над горизонтальной стеной, других стен нет надо | Робот под стеной, на клетку ниже исходного положения нач цел n n:=0 нц пока снизу стена I вправо; n:= n + 1 кц вниз влево кц Кон При выполнении этого алгоритма компьютер сначала присвоит величине п значение 0 (команда n:= 0). Затем в цикле компьютер будет командовать Роботу вправо и тут же увеличивать значение п на 1 (команда n:= n + 1). После каждого выполнения тела цикла значение п окажется равным числу сделанных Роботом шагов вправо. После окончания цикла значением п будет общее число сделанных вправо шагов. Поэтому, при выполнении нц n раз компьютер п раз скомандует влево, Робот окажется в точности на клетку ниже исходного положения (рис. 58).
Рис. 58
Рисование параболы
Рассмотрим следующую задачу: изобразить с помощью Чертежника график функции (параболу) у = х2. Условие этой задачи нуждается в уточнении. Во-первых, нарисовать весь график нельзя — ведь он бесконечен. Поэтому будем рисовать только его часть, например от х = 0 до х = 2. Во-вторых, Чертежник не умеет рисовать ничего, кроме отрезков, а график функции у = х2 — это кривая. Поэтому параболу придется заменить ломаной. Если вершины ломаной лежат на параболе и звенья ломаной очень короткие, то ломаная на вид почти не отличается от параболы. На рисунке 59, а ломаная имеет 4 звена, на рисунке 59, б — 10 звеньев, на рисунке 75, в — 100 звеньев.
Рис. 59
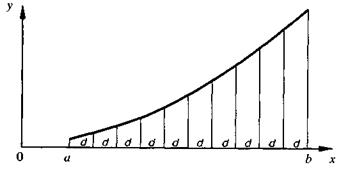
В общем случае с помощью Чертежника можно изобразить параболу на некотором участке (от а до b) в виде ломаной из какого-то числа звеньев (п). Будем рисовать ломаную слева направо, начиная от точки (а,а**2) и кончая точкой (b,b**2). От вершины к вершине будем перемещаться с помощью команды Чертежника сместиться в точку. Используем вещественную величину х для запоминания x-координаты очередной вершины ломаной. Разобьем отрезок от а до b на п равных частей длины d = (b -а)/п (рис. 60). При рисовании очередного звена ломаной величину х надо просто увеличивать на d — это можно сделать с помощью команды присваивания х:= х + d:
алг парабола (арг вещ а, b, арг цел n) дано n > 0 | перо Чертежника поднято надо | нарисован график функции у = х**2 на участке от а до b | в виде ломаной из n звеньев; перо в точке (b, b**2) и поднято нач вещ х, d х:= а; d:= (b - а)/n сместиться в точку (а, а**2) опустить перо нц n раз х:= х + d сместиться в точку(х, х**2) кц поднять перо Кон При выполнении вызова "парабола (0, 2, 10)" компьютер выдаст Чертежнику последовательно 13 команд: сместиться в точку (0, 0) опустить перо сместиться в точку (0.2, 0.04) сместиться в точку (0.4, 0.16) сместиться в точку (0.6, 0.36) сместиться в точку (0.8, 0.64) сместиться в точку (1.0, 1.00) сместиться в точку (1.2, 1.44) сместиться в точку (1.4, 1.96) сместиться в точку (1.6, 2.56) сместиться в точку (1.8, 3.24) сместиться в точку (2.0, 4.00) поднять перо и Чертежник нарисует параболу на участке от 0 до 2 в виде ломаной из 10 звеньев.
Рис.60.
ЗАДАЧИ И УПРАЖНЕНИЯ 1. Значение величины х равно 3. Чему оно будет равно после выполнения команды: а) х:= 5; б) х:= х + 5; в) у:= х?
2... После выполнения команды а) х:= х+5; б) х:=-х; в) у:= х
или серии команд
г) у:= 1; х:= х + у; д) у:= х; х:= у
значение величины х стало равно 3. Чему было равно значение величины х до выполнения в каждом из этих случаев?
3. После выполнения команды присваивания х:= х + у значение величины х равно 3, а значение у равно 5. Чему были равны значения величин х и у до выполнения команды?
4. Значение величины х равно а, значение у равно b. После выполнения каких из указанных ниже последовательностей команд значения величин х и у поменяются, т. е. х станет равно b, а у станет равно а? а) х:= у б) t:=х в) х:= х + у г) t:= х y:= х х:= у у:= х - у у:= t у:= t х:= х - у х:= у
5. Опишите, что произойдет при выполнении алгоритма "вниз сквозь стену" для начальных положений Робота, указанных на рисунке 61.
Рис. 61
6. Дан алгоритм:
дано n > 0 I перо Чертежника поднято надо | нарисован график некоторой функции на участке от 0 | до b в виде ломаной из n звеньев; перо в конце графика и поднято нач вещ х,d, v х:= 0; b := b /n сместиться в точку (0, 0) опустить перо нц n раз v:= 2*х*d + d*d; х:= х + d сместиться на вектор (d, v) кц поднять перо Кон а) Как будет выглядеть память ЭВМ при выполнении вызова "график(2, 10)"? б) Что нарисует Чертежник при выполнении этого вызова?
7. Робот находится перед входом в тупик, идущий вправо. Составьте алгоритм, при выполнении которого с помощью Чертежника будет нарисован график радиоактивности в тупике (считая, что единица масштаба по оси Ох равна размеру клетки на поле Робота).
8. Составьте алгоритмы со следующими заголовками: а) алг вниз до стены закрасить и вернуться дано | где-то ниже Робота есть стена надо | Робот дошел до этой стены, закрасил клетку | и вернулся в исходное положение
б) алг закрасить клетку в правом нижнем углу дано |Робот где-то внутри прямоугольника, огороженного стенами, других стен нет надо |Робот закрасил клетку в правом нижнем углу |прямоугольника и вернулся в исходное положение
в) алг отойти вдвое дальше от левой стены дано |где-то левее Робота есть стена, других стен нет надо | Робот отошел вправо на расстояние от стены вдвое большее, чем исходное
г) алг симметрия дано |где-то ниже Робота есть горизонтальная стена длиной в одну клетку, других стен нет надо |Робот оказался в положении, симметричном исходному относительно стены
д) алг симметрия дано |где-то ниже Робота есть горизонтальная стена, |которая и вправо и влево кончается, других стен нет надо |Робот оказался в положении, симметричном исходному относительно стены
е) алг обойти прямоугольное препятствие дано | Робот над прямоугольником, огороженным стенами, других стен нет надо | Робот под прямоугольник
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 811; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.149.148 (0.016 с.) |


 сместиться в точку (1,1)
сместиться в точку (1,1) опустить перо
опустить перо

 опустить перо
опустить перо домик; сместиться на вектор (6, 0)
домик; сместиться на вектор (6, 0)
 сместиться в точку (2, 1)
сместиться в точку (2, 1) опустить перо
опустить перо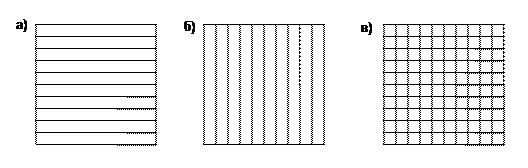
 опустить перо
опустить перо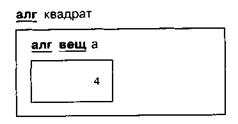
 опустить перо
опустить перо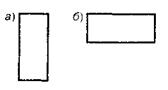
 нц n раз
нц n раз нц n раз
нц n раз нц m раз
нц m раз Измените алгоритм "виток" (А46) так, чтобы спираль в алгоритме А45 раскручивалась против часовой стрелки.
Измените алгоритм "виток" (А46) так, чтобы спираль в алгоритме А45 раскручивалась против часовой стрелки.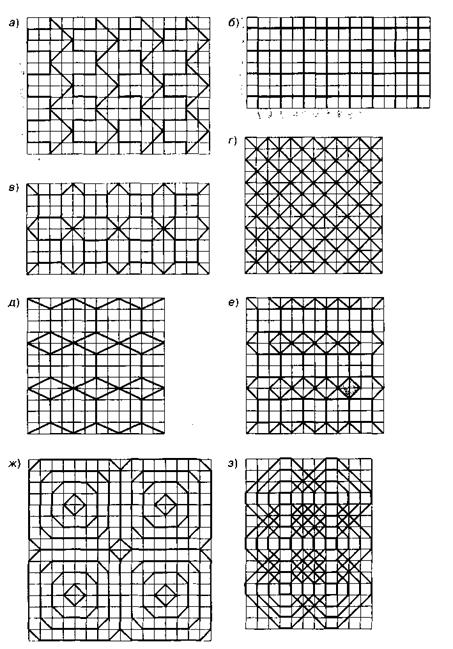

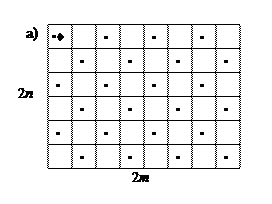
 опустить перо
опустить перо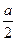 ,
,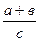 и т. д.
и т. д.