Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Квадрат суммы и квадрат разности (Макарычев Ю.Н., Ершова А.П.)
Похожие статьи вашей тематики
1 уровень сложности (базовый):
| Вариант 1.
| Вариант 2.
| | 1. Выполнитедействия:
| | а) (4+а)2;
| б) (2х-1)2;
| а) (5+х)2;
| б) (1-3х)2;
| | в) (2а+3b)2;
| г) (х3-3)2.
| в) (3а-10b)2;
| г) (х2+4)2.
| | 2. Представьте трёхчлен в виде квадрата двучлена:
| | а) х2+6х+9;
| б) 25х2-10х+у2.
| а) 4+4а+а2;
| б) а2-8ab+16b2.
| | 3. Упростите выражения:
| | а) (4х+3)2-24х;
| б) 18с2-2  (3с-1)2. (3с-1)2.
| а) (2х-5)2+20х;
| б) 6с2-3  (1+6с)2. (1+6с)2.
| 2 уровень сложности («на четвёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Выполнитедействия:
| | а) (11-х)2;
| б) (2х+0,5)2;
| а) (y+15)2;
| б) (5x-0,2)2;
| | в) (-3а+3b)2;
| г) (а2+b3)2.
| в) (-2а+7b)2;
| г) (a3+b4)2.
| | 2. Представьте трёхчлен в виде квадрата двучлена:
| | а) х2+49-14x;
| б) 25y2+20хy+4x2.
| а) 12x+x2+36;
| б) 16x2-24xy+9y2.
| | 3. Упростите выражения:
| | а) (5х-3y)2+30хy;
| б) 4x4-2(x4+1)2.
| а) (6a+2b)2-24ab;
| б) –6x3-3(x3-1)2.
| 3 уровень сложности («на пятёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Выполнитедействия:
| а) (2y+  )2; )2;
| б) (-7х-1)2;
| а) (3x- 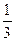 )2; )2;
| б) (-6x-1)2;
| | в) (а2 -2b)2;
| г) (8x+x3)2.
| в) (4а-b2)2;
| г) (x4-9x)2.
| | 2. Представьте трёхчлен двумя способами в виде квадрата двучлена:
| | а) 100х2+1-20x;
| б) x4+4y2+4x2y.
| а) 1+81y2-18y;
| б) 8ab3+16a2+b6.
| | 3. Раскройте скобки:
| | а) (3a-b)2-(3a+b)2;
| б) (a+(b-c))2.
| а) (2x+y)2-(2x-y)2;
| б) (c-(a+b))2.
|
§ 2. Преобразование целого выражения в многочлен (Макарычев Ю.Н., Ершова А.П.)
1 уровень сложности (базовый):
| Вариант 1.
| Вариант 2.
| | 1. Упростите выражения
| | а) (3-a)(3+a);
| б) (b-2a)(2a-b);
| а) (a-4)(a+4);
| б) (5x+y)(y-5x);
| | в) (x2 -1)(1+x2).
|
| в) (1-x3)(x3+1).
|
| | 2. Разложите на множители:
| | а) y2-100;
в) a4-25.
| б)- 0,16x2+y2;
| а) 49-x2;
в) 9-a4.
| б) –0,01a2+b2;
| | 3. Решите уравнения:
| | а) (x-1)(x+1)-x(x-2)=0;
| б) x2-4=0.
| а) (x+2)(x-2)-x(x-2)=0;
| б) x2-1=0.
| | 4.Представьте в виде произведения:
| | а) y3+8;
| б) a3-1.
| а) y3+1000;
| б) b3-8.
| | | | | | | | 2 уровень сложности («на четвёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Упростите выражения:
| | а) (x-2)(x+12);
| б) (3a+2b)(2b-3a);
| а) (14+x)(14-x);
| б) (5a+3b)(3b-5a);
| | в) (-4n3 +n)(n+4n3).
|
| в) (2n2+n)(-2n2+n).
|
| | 2. Разложите на множители:
| | а) 400-y2;
в) (x+1)2-4.
| б)- 0,25x2+y2z2;
| а) x2-121;
в) (x-1)2-9.
| б) –0,04a2+b2c2;
| | 3. Решите уравнения:
| | а) x2-(x+3)(x-3) =3x;
| б) 4x2-9=0.
| а) x2-(x-4)(x+4) =2x;
| б) 25x2-16=0.
| | 4.Представьте в виде произведения:
| | а)27x3-y3;
| б) y3+64.
| а)8a3+y3;
| б) x3-125.
| | | | | | | | | |
3 уровень сложности («на пятёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Упростите выражения
| | а) (5a+0,2)(0,2-5a);
б) (-6a-2b)(6a-2b);
в) (b2+4)(b-2)(b+2).
| а) (10x+0,3)(0,3-10x);
б) (7a-3b)(-7a-3b);
в) (x2+9)(x+3)(x-3).
| | 2. Разложите на множители:
| | а) –a4+16;
в) (3x-3)2-(x+2)2.
| б) 64x2-(x-1)2;
| а) -a4+81;
в) (3x-2)2-(x+1)2.
| б) 25x2-(x+y)2;
| | 3. Решите уравнения:
| а) (2x-1)2-4(x-2)(x+2) =0;
б)  x2=0,16. x2=0,16.
| а) (3x+1)2-9(x+1)(x-1) =0;
б)  x2=0,81. x2=0,81.
| | 4.Представьте в виде произведения:
| | а)8x3+0,064y3;
| б) x3-64.
| а)27x3+0,008y3;
| б) 1-x6.
| | | | | | |
Способы разложения на множители (Макарычев Ю.Н.,
Ершова А.П.)
1 уровень сложности (базовый):
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | а) 2y2-18;
| б) 2x2-12x+18.
| а) 3y2-27;
| б) 3x2+12x+12.
| | 2. Упростите выражения:
| | а) (2a+3)(a-3)-2a(4+a);
б) (1-x)(x+1)+(x-1)2.
| а) (5-a)(3a+1)-3a(4-a);
б) (2-x)(x+2)+(x+2)2.
| | 3. Докажите тождество:
| | а) x4-27x=(x2-3x)(x2+3x+9).
| а) x5+8x2=(x2+2x2)(x2-2x+4).
| | | | | |
2 уровень сложности («на четвёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | а) 64a-a3;
| б) x3-10x2+25x.
| а) y5-25y3;
| б) 16x+8x2+x3.
| | 2. Упростите выражения:
| | а) (a+b)(a-2b)+(2b-a)(2b+a);
б) (3x+2)2-(3x-1)2.
| а) (3a-b)(a+b)+(b-3a)(b+3a);
б) (2x+3)2-(2x-1)2.
| | 3. Докажите тождество:
| | а) (x2+3)2=(x2-3)(x2+3)+6(x2+3).
| а) (4-x2)2=(4-x2)(4+x2)+2x2(x2-4).
| | | | | | 3 уровень сложности («на пятёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | a) x3-xy2-6y2+6x2;
| б) 8x4y-xy4.
| a) a3-2a2+18-9a;
| б) a5b2+27a2b5.
| | 2. Упростите выражения:
| | а) (2x+3)(2x-1)-(2x+1)(2x-1);
б) (3a-3b)2-3(a-b)2.
| а) (3x+1)(x-1)-(3x-1)(3x+1);
б) (2a+2b)2-2(a+b)2.
| | 3. Докажите тождество:
| | а) (a2+4)2-16a2=(a+2)2(a-2)2.
| а) (4a+1)2(4a-1)2=(16a2+1)2-64a2.
| | | | | |
§ 4. Все действия с многочленами (домашняя самостоятельная работа) (Макарычев Ю.Н., Ершова А.П.)
| 1. Разложите на множители:
| | а) 30x-9x2-70y+49y2;
б) 20a2-45b2+30b-5;
в) x4+4x2+3;
г) a2-3ab+2b2;
д) 28x3-3x2+3x-1.
| а) 64x2-48x-25y2-30y;
б) 18a224a+8-200b2;
в) x4+8x2+15;
г) a2+4ab+3b2;
д) 126x3+3x2+3x+1.
| | 2. Докажите, что при любых значениях переменных многочлен
| | x2+2x+y2-4y+5
| x2-4x+y2+6y+13
| | принимает неотрицательные значения.
| | 3. Решите уравнения:
| )  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  ;
д) ;
д)  ;
е) ;
е)  . .
| а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  ;
д) ;
д)  ;
е) ;
е)  . .
| | 4. Докажите, что при любом натуральном n
| | а) (n2+n)(n+2) кратно 3;
б) n3-n кратно 6;
в) если n2-1 чётно, то n2-1 делится на 8;
г) 5n-1 кратно 4;
д) если n нечётно, то 1+2n+7n+8n кратно 9.
| а) 8n3-2n кратно 3;
б) (n2+n)(n+5) кратно 6;
в) если n3-4n чётно, то n3-4n делится на 48;
г) 10n-1 кратно 9;
д) если n нечётно, то 6n+4n+3n+1 кратно 7.
|
§ 5. Формулы a2-b2, (a+b)2 и (a-b)2 (Зив Б., Гольдич В.А.)
1 уровень сложности (базовый):
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | а) 9а2-16;
| б) х2-8ах+16а2;
| а) 25-16x2;
| б) 9x2+6x+1;
| | в) -4-4а-а2;
| г) (а+2b)2-(3a-b)2.
| в) -16a2+8a-1;
| г) (a-3b)2-(a+2b)2.
| | 2. Решите уравнение:
| | (x-2)2-(x-1)(x+1)=0
| (x+3)2-(2-x)(2+x)=0
| | 3. Вычислите:
| 872-174  67+672 67+672
| 2022-542+256  352 352
| 2 уровень сложности («на четвёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | а) 25a2-(a+b)2;
б) a4+2a2b+b2;
в) -x4-2nx2-n2;
г) 16(x-y)2-25(x+y)2.
| а) 4x2-(3x-2y)2;
б) x4-2b2x2+b2;
в) -9c2+12cd2-4d4;
г) 49(2m-3n)2-9(m+n)2
| | 2. Решите уравнение:
| | (3x-1)2-8(x+1)2=(x+2)(x-2)
| (2x+1)2-3(x-5)2=(x+3)(x-3)
| | 3. Вычислите:
| 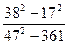
| 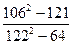
| 3 уровень сложности («на пятёрку»):
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | а) 25m2+30mn+9n2;
| а) 9a2+48ab+64b2;
| | б) y2-10y+25-4m2.
| б) x2+8x+16-9a2.
| | 2. Докажите, что
| | (ab-1)2+(a+b)2=(a2+1)(b2+1)
| (1-m)(1-m2)+m(m+1)=m3+1
| | 3. Упростите
| | (a+2b)(a-2b)(a2+4b2)
| (x-3y)(x+3y)(x2+9y2)
| | 4. Докажите, что при всяком натуральном n выражение (n2+3n+1)2-1 делится без остатка на 24
| 4. Докажите, что квадрат всякого нечётного числа, уменьшенный на единицу, делится на 8.
| | 5. Вычислите
| | (x+y)2+2x+2y+1 при х=3,74, у=1,26
| (a+b)2+4a+4b+4 при a=5,37, b=2,63
| 4 уровень (для тех, кто увлечён математикой):
| Вариант 1.
| Вариант 2.
| | 1. Докажите, что
| | (a+b+c)2=a2+b2+c2+2ab+2ac+2bc
| (x+y-z)2=x2+y2+z2+2xy-2xz-2yz
| | 2. Разложите на множители:
| | а) a2-b2-c2+2bc;
| а) (x+3y)2-y2+2xy-x2;
| | б) a2b+b2c+ac2-ab2-bc2-a2c
| б) a4+b4+2a3b+2a2b2+2ab3.
| | 3. Решите уравнение:
| | (3+x)2+(5-2x)(5+2x)-3(5-x2)=1
| -6(2+m)(2-m)+(5-m)2-m(7m-1)=0
| | 4. Некоторое натуральное число при делении на 5 дает в остатке 1, а другое число при делении на 5 дает в остатке 2. Докажите, что сумма квадратов этих чисел делится на 5.
| 4. Натуральное число при делении на 11 дает в остатке 4. Докажите, что его квадрат при делении на 11 дает в остатке 5.
| | 5. Докажите, что многочлен
| | 3a2+3b2+3c2-2ab-2ac-2bc
| 2x2+2y2+13z2-2xy+4xz-6yz
| | принимает неотрицательные значения при любых численных значениях входящих в него букв.
|
§ 6. Формулы a3-b3, a3+b3 (Зив Б., Гольдич В.А.)
| Вариант 1.
| Вариант 2.
| | 1. Разложите на множители:
| | 27-с3
| 64-а3
| | 2. Выполните умножение:
| | а) (x+4)(x2-4x+16)
| а) (x+3)(x2-3x+9)
| | б) (5m+3n)(25m2-15mn+9n2)
| б) (4x-5y)(16x2+20ax+25y2)
| | в) (2a-3x)(4a2+6ax+9x2)
| в) (3x+5y)(9x2-15xy+25y2)
| | 3. Раскройте скобки:
| | (3x2-2)(9x4+6x2+4)
| (5x2+3)(25x4-15x2+9)
|
|



 (3с-1)2.
(3с-1)2.
 )2;
)2;
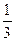 )2;
)2;
 x2=0,81.
x2=0,81.
 ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
д)
;
д)  ;
е)
;
е)  .
.
 ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
д)
;
д)  ;
е)
;
е)  .
.