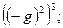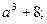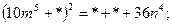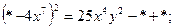Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выделяются два типа дифференциации обучения: внешняя и внутренняя.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внешняя дифференциация - это разделение учащихся по определенным признакам (способностям, интересам) на стабильные группы, в которых и содержание образования и методы обучения, и организационные формы различаются. Внутренняя (внутриклассная) дифференциация учитывает индивидуальные особенности детей в процессе проведения самостоятельной работы. Разделение на группы может быть явным или неявным, состав групп меняется в зависимости от поставленной задачи. В дифференциации по типу “внутриклассной” выделяются следующие виды: дифференциация по способностям, дозирование помощи учителя, уровневая дифференциация. Внутренняя дифференциация существует обычно в форме индивидуального подхода к учащимся, когда учитываются их психофизиологические особенности - память, мышление, темперамент и т.д. Обучаясь в одном классе по одной программе и учебнику, школьники могут усваивать материал на различных уровнях. Определяющим уровнем при этом является уровень обязательной подготовки. На его основе формируются более высокие уровни овладения материалом. По отношению к этому виду дифференциации в последнее время получил распространение термин “уровневая дифференциация”. Организуя дифференцированную работу при выполнении самостоятельной работы, учитель должен ясно представлять: ü закреплению каких навыков и приемов учебной деятельности служит предложенное ученику задание? ü какие виды заданий необходимо отрабатывать? ü какие ученики нуждаются в помощи учителя, и в какой форме предложить эту помощь? ü какие ученики, и в каком объеме могут выполнять задания творческого характера? Решение этих проблем при помощи дифференцированных заданий способствует как закреплению учебного материала, так и умственному развитию учащихся в процессе обучения.
1.2. Организация самостоятельной работы при Изучении нового материала Психологи исследовали учебную деятельность и установили, что изучения каждого самостоятельного раздела или темы учебной программы должно состоять из следующих трех основных этапов: 1) Вводно-мотивационный этап. На этом этапе учащиеся должны осознать основную цель предстоящего изучения учебной темы, ее место и роль в общем образовании, ее практическое и теоретическое значение. В нужных случаях, учитель указывает, какие знания, и умения ранее пройденного материала особенно понадобятся при изучении данной темы. Затем учитель сообщает, сколько уроков отведено на изучение темы, примерные сроки ее завершения и перечисляет основные элементы темы, т.е. знания, умения и навыки, которыми должны овладеть учащиеся в результате изучения этой темы.
2) Операционно-познавательный этап. На этом этапе учащиеся усваивают знания, входящие в содержание данной темы, при этом используются разные виды и формы учебной работы: рассказ или лекция, фронтальная работа по изучению понятия. Коллективная работа по усвоению учебного материала, решению задач, проведению опытов и экспериментов, индивидуальная работа по решению задач, и т.д. Изложение учебного материала производится в основном учителем, но по мере взросления учащихся, часть учебного материала передается для изложения докладчиком или для индивидуального изучения и проработке по учебнику. 3 ) Рефлексивно-оценочный этап. Здесь производится обобщение изученного и подведение итогов работы по данной теме. При этом, главная цель этого этапа – развитие у учащихся рефлексивной деятельности (самоанализа), способностей к обобщению и формирование адекватной самооценки. Для обобщения пройденного материала могут использоваться различные методы: обобщающие уроки, доклады учащихся, составление по группам обобщающих схем. Для того чтобы самостоятельная работа учащегося была эффективной, необходимо выполнить ряд условий, к которым можно отнести следующие: - обеспечение правильного сочетания объемов классной и самостоятельной работы; - методически правильная организация работы учащегося в классе и в домашней работе; - обеспечение учащегося необходимыми методическими материалами с целью превращения процесса самостоятельной работы и мерами, поощряющими учащегося за ее качественное выполнение. На наш взгляд, возможны два направления построения учебного процесса на основе самостоятельной работы учащегося. Первый – это увеличение роли самостоятельной работы в процессе классных занятий. Реализация этого пути требует от учителей разработки методик и форм организации классных занятий, способных обеспечить высокий уровень самостоятельности учащегося и улучшения качества подготовки.
Второй – повышение активности учащихся по всем направлениям самостоятельной работы во внеаудиторное время, которое связано с рядом трудностей. В первую очередь, это – неготовность учащихся в профессиональном и психологическом плане. Несмотря на важную роль, которую выполняет самостоятельная работа в учебном процессе, многие учащиеся не умеют правильно ее организовать. Отсюда встают вопросы о психологической готовности учащихся к данному виду деятельности, об умении и условиях заниматься ею. Мы выяснили, что самое трудное для учителя в этой системе научиться организовывать самостоятельную деятельность классного коллектива, постепенно передавать учащимся многие свои функции и роли, и, не подавляя инициативы, руководить самостоятельной работой учащихся. Как показывает опыт, если эту систему вводить, начиная с первого класса, то учащиеся быстро осваиваются с ней, и она становится для них привычной, и школьники смогут в полной мере испытать чувства эмоционального удовлетворения от сделанного, радость победы над преодоленными трудностями, счастье познания нового, интересного. Тем самым будет формироваться у учащихся ориентация на переживание таких чувств в будущем, что приведет к возникновению потребности в творчестве, познании, в упорной самостоятельной учебе.
§2. Домашняя самостоятельная работа Определённую роль в воспитании самостоятельности, настойчивости, умения работать с книгой играют домашние самостоятельные работы, которые даются наряду с текущими домашними заданиями [33,44]. Развитие творческих способностей, формирование умений самостоятельно работать происходят как на уроке, так и в домашних условиях при выполнении домашних самостоятельных работ. Домашняя самостоятельная работа – это особый вид самостоятельной работы. Он происходит без непосредственного руководства учителя, поэтому нуждается в создании необходимых условий для успешного выполнения. Цель домашних самостоятельных работ нередко сводится к закреплению знаний, умений и навыков, полученных в классе. Эта цель важна, но нельзя ограничиваться только ею. Учащиеся, воспринимая новый материал на уроке, стремяться понять его, связать с уже известным, найти ему применение. Осуществить всё это в краткие сроки не всегда удается. Поэтому задачей домашней самостоятельной работы является углубленное понимание расширенного в школе материала или творческое применение его в данной ситуации. В домашних самостоятельных работах необходимо предусматривать задания не столько на простое воспроизведение изученного, сколько на применение усваиваемых правил, приёмов, понятий в новых ситуациях, а также новое комбинирование материала, его видоизменение, придумывание самостоятельных примеров. Домашние самостоятельные работы должны быть маловариантны, что позволяет осуществлять дифференцированный подход к учащимся и, вместе с тем, обеспечивает самостоятельность их выполнения. Срок выполнения работы зависит от объёма и степени трудности. Домашние самостоятельные работы преследуют следующие цели: ü привести в систему материал какого – либо раздела, проследить линию вопроса по программе разных классов, обеспечивая необходимое повторение материала;
ü развитие мышления учащихся; ü воспитание культуры умственного труда; ü предупреждение отставания учащихся; ü расширение и углубление знаний; ü воспитание интереса к математике; ü развитие самостоятельности учащихся и др. Каждая цель может распадаться на более мелкие, уточняющие цели. Правильная организация домашней самостоятельной работы способствует выработке у учащихся трудолюбия, настойчивости, дисциплинированности и самостоятельности. Всего существует три основных уровня домашней самостоятельной работы: 1. Обязательный минимум. Главное свойство этого задания: оно должно быть абсолютно понятно и посильно любому ученику. 2. Тренировочный. Его выполняют ученики, которые желают хорошо знать предмет и без особых трудностей осваивают программу. 3. Творческое задание. Среди творческих заданий можно выделить некоторые типовые группы: ü частушки, басни, сказки, фантастические рассказы по учебным темам; ü чайнворды, кроссворды и т. п.; ü тематические сборники интересных фактов, примеров и задач; ü сборники аннотаций на статьи по выбранной теме и др. Важной особенностью домашней самостоятельной работы является следующее: выполнить домашнюю самостоятельную работу легче и быстрее в тот день, когда её задали. Во многих школах практикуют разнообразные эффективные виды домашних самостоятельных работ по математике: закрепление нового материала по учебнику, решение упражнений и задач, работа над ошибками, домашние контрольные работы, сочинения, лабораторные и практические работы, моделирование, подготовка докладов, сбор числового материала из газет, журналов, различных сборников, подбор интересных задач к теме из дополнительной литературы, написание рефератов и др. Н.Н. Поспелов [35,56] выделяет следующие виды домашних самостоятельных работ. Рассмотрим некоторые из них: 1. Здание массивом. Задаётся большой массив задач – в рамках большой изучаемой или повторяемой темы. Из массива заданий ученик выбирает тот уровень сложности, который способен выполнить. При выполнении домашних самостоятельных работ массивом происходит самосогласование ребёнка и уровня задач, которые он решает. 2. Особое задание. Более способные ученики получают право на выполнение особо сложного задания. Задание выполняется в специальной тетради, включает в себя тренировочные и творческие задачи повышенной сложности.
3. Сочинение. Выполняя такое задание, учащиеся проделывают очень полезную работу: изучают учебную и научно – популярную литературу по теме, отбирают из большого объёма материала необходимый минимум. Сочинения пишут на заданные учителем темы. Пример домашней самостоятельной работы приведен в приложении §4. §3. Организация самостоятельной работы на уроках алгебры Самостоятельная работа учащихся (работа в отсутствии учителя или, по крайней мере, без обращения к его помощи в течение длительного промежутка времени) традиционно использовалась в обучении для закрепления изученного под руководством учителя теоретического материала по учебнику и тренировочных работ по его изучению. В процессе совершенствования самостоятельной работы в направлении обучения в это понятие стали вкладывать разный смысл: как метод обучения Г.И. Саранцев определяет самостоятельную работу как многоаспектное явление обучения, обладающее следующими признаками [44]: ü быть одним из методов обучения; ü являться одной из форм организации познавательной деятельности; ü быть одним из средств обучения; являться одним из видов деятельности; ü быть самостоятельной деятельностью учения. Эти закономерности организации самостоятельной работы учащихся в обучении нашли широкое отражение в методике обучения математике, как в теоретическом, так и в практическом плане в работах Ф.М. Барчуновой, Самостоятельную деятельность учащихся можно и нужно организовывать на различных уровнях: от воспроизведения действий по образцу и узнавания объектов путем их сравнения с известным образцом до составления модели и алгоритма действий в нестандартных ситуациях. Учителю необходимо учитывать, что при составлении заданий для самостоятельной работы степень сложности должна отвечать учебным возможностям детей. Переход с одного уровня на другой должен осуществляться постепенно, только когда учитель будет убежден, что учащийся справится со следующим уровнем самостоятельности. Иначе в атмосфере спешки и нервозности у ученика возникают пробелы в знаниях. Очень важно, чтобы содержание самостоятельной работы, форма и время ее выполнения отвечали основным целям обучения данной теме на данном этапе. В то же время учителю нужно знать, что злоупотребление самостоятельной работой в учебном процессе также вредно, как и ее недооценка. Бывает так, что учитель включает в урок самостоятельную работу без особой необходимости, просто ради разнообразия, не продумав ее содержание и форму организации. Результаты бывают плачевны: или дети не готовы выполнить задание, или не хватило времени и т. п., а в результате - зря потрачено драгоценное время урока. Но если, составляя план урока, учитель тщательно продумал место и время самостоятельной работы, четко определил ее общее содержание, разбил задания по разным уровням сложности, то она сыграет свою положительную роль.
Для того чтобы самостоятельная работа сыграла свою роль в учебном процессе нужно сначала определить форму и вид данной самостоятельной работы. В зависимости от целей, которые ставятся перед самостоятельными работами, они могут быть: обучающими, тренировочными, закрепляющими, повторительными, развивающими, творческими, контрольными. Разберем подробнее каждый вид самостоятельных работ. Смысл обучающих самостоятельных работ заключается в самостоятельном выполнении школьниками данных учителем заданий в ходе объяснения нового материала. Цель таких работ – развитие интереса к изучаемому материалу, привлечение внимания каждого ученика к тому, что объясняет учитель. Здесь сразу выясняется непонятное, выявляются сложные моменты, дают себя знать пробелы в знаниях, которые мешают прочно усвоить изучаемый материал. Самостоятельные работы по формированию знаний проводятся на этапе подготовки к введению нового содержания, а также при непосредственном введении нового содержания, при первичном закреплении знаний, т.е. сразу после объяснения нового, когда знания учащихся еще непрочны. Учителю необходимо знать следующие особенности обучающих самостоятельных работ: их надо составлять в основном из заданий репродуктивного характера, проверять немедленно и не ставить за них плохих оценок. Так как самостоятельные обучающие работы проводятся во время объяснения нового материала или сразу после объяснения, то их немедленная проверка дает учителю четкую картину того, что происходит на уроке, какова степень понимания учащимися нового материала на самом раннем этапе его изучения. Цель этих работ – не контроль, а обучение, поэтому им следует отводить много времени на уроке. Например: ü Вставьте пропущенные слова так, чтобы получилось верное высказывание: «Квадрат суммы равен квадрату …, плюс... первого на …, плюс …» ü Используя формулу сокращенного умножения, преобразуйте выражение: (m+n)(m-n); x2-y2; 4-4a+a2; (a-2)(a2+2a+4). ü Какие из равенств являются тождествами: x3-y3=(x-y)(x2+xy+y2); x3+125=(x+5)(x2-5x+25). ü Разложите на множители выражение: 8-a3; m3+n3; 125a3-y3. ü Закончите решение: (2+x)2=22+2 При выполнении самостоятельных тренировочных работ учащимся еще необходима помощь учителя. Можно разрешить пользоваться учебником, записями в тетрадях, таблицами и т. п. все это создает благоприятный климат для слабых учащихся. В таких условиях они очень легко включаются в работу и выполняют ее. К таким работам можно отнести выполнение заданий по разноуровневым карточкам. Сейчас такие дидактические материалы выпущены и по алгебре, и по геометрии для всех классов. По этим карточкам учащиеся привыкают работать самостоятельно. В последствии некоторые учащиеся, выполнив свое задание, хотят попробовать решить задание более высокого уровня. Постепенно учащиеся привыкают не бояться трудностей и стремятся к более высокой самооценке. В приложении, в §5, приведен пример самостоятельной тренировочной работы по 4 уровням сложности, составленной по теме «Формулы a2-b2, (a+b)2 и (a-b)2». К закрепляющим можно отнести самостоятельные работы, которые способствуют развитию логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно, осмысленно усвоен учебный материал. По результатам проверки заданий данного вида учитель определяет, нужно ли еще заниматься данной темой. Примером таких работ в изобилии встречаются в различных дидактических материалах. ü Проверить, верны ли следующие равенства: (c+d)2=c2+2cd+d2; (m-n)2=m2-2mn+n2 ü Написать квадрат первого числа каждого из следующих квадратов суммы: (x+y)2; (1+p)2; (2a3+1)2 ü Написать удвоенные произведения первого числа на второе каждого из следующих квадратов разности: (l-y)2; (1-h)2; (3a3-1)2 Очень важны так называемые повторительные (обзорные или тематические) работы. Перед изучением новой темы учитель должен знать, подготовлены ли школьники, есть ли у них необходимые знания, какие проблемы смогут затруднить изучение нового материала. Например: ü Выполните действия: (4+а)2; (2х-1)2 ü Представьте трёхчлен в виде квадрата двучлена: х2+6х+9; 25х2-10х+у2 ü Упростите выражения: (4х+3)2-24х; 18с2-2 Самостоятельными работами развивающего характера могут быть домашние задания по составлению докладов на определенные темы, подготовка к олимпиадам, научно-творческим конференциям, проведение в школе “дней математики”, сочинение математических игр, спектаклей, сказок и т. д. На уроках – это самостоятельные работы, требующие умения решать исследовательские задачи. Большой интерес вызывают у учащихся самостоятельные творческие работы, которые предполагают высокий уровень познавательной самостоятельности. Здесь учащиеся открывают для себя новые стороны уже имеющихся у них знаний, учатся применять эти знания в нестандартных ситуациях. Например: ü не решая пример, скажите, корректно (да) или некорректно (нет) следующее задание: а) разделите многочлен 3х2у-9ху2 на одночлен 3х2у; б) разделите многочлен 3xyz-9xy2z на одночлен 3xy; ü найдите многочлен А, если известно, что х3-125=А(х-5). Вычислите значение многочлена А при х=1. Контрольные работы являются необходимым условием достижения планируемых результатов обучения. По существу разработка текстов контрольных работ должна быть одной из основных форм фиксирования целей обучения, в том числе и минимальных. По этому, во-первых, контрольные задания должны быть равноценными по содержанию и объему работы; во-вторых, они должны быть направлены на отработку основных навыков; в-третьих, - обеспечивать достоверную проверку уровня обучения; в-четвертых, они должны стимулировать учащихся, позволять им продемонстрировать прогресс в своей общей подготовке [см. приложение §7].
Рассмотрим некоторые виды самостоятельных работ, которые использую в своей практике. Самостоятельные работы с целью актуализации знаний учащихся проводятся перед введением нового материала и перед закреплением его. Данная работа может быть воспроизводящей и реконструктивно-вариативной. Работе воспроизводящего характера (по образцу, по инструкции или алгоритму, с промежуточными записями, с указаниями к решению и др.) способствует психологический настрой на успех. На этом уровне происходит подготовка к самостоятельной деятельности. Работы по инструкции или алгоритму применяются для закрепления изученного материала, соответствует низкому уровню самостоятельности, может применяться для учащихся с любым уровнем обучаемости. Например, разложим на множители многочлен Алгоритм решения: 1. Вынесем за скобки общий множитель; 2. Разложим на множители многочлен, который получился; 3. Сгруппируем члены многочлена; 4. Запишем окончательно то, что получилось. Самостоятельная работа с промежуточными записями содержит решение упражнений или доказательство теоремы с пропусками. Учащиеся должны восстановить недостающие записи, выводы, вычисления и т.д. Например, 1)Допишите недостающие слова. «Разность квадратов … выражений равна ….. разности этих выражений и их …» 2) Упростите выражение: Самостоятельная работа с выборочной системой ответа заключается в том, что даются несколько вариантов ответа, из которых учащиеся выбирают верный (подчеркивают или выписывают). Например, Упростите выражение 1) 2) 3) Вариант ответов:
Математический диктант может носить как контролирующий, так и обучающий характер, требует краткого ответа и несложных вычислений. Математический диктант по теме «Возведение в квадрат суммы и разности двух выражений» 1. Напишите формулу квадрата суммы. 2. Представьте в виде многочлена: а) 3. Упростите выражение: 4. Найдите значение выражения: «Экспресс-диктант» проводится как и обычный диктант, но ответы записываются в двух экземплярах (под копирку). Контрольный экземпляр сдается учителю, по оставшемуся экземпляру идет фронтальная проверка. Большой интерес вызывают у учащихся творческие самостоятельные работы, которые предполагают высокий уровень самостоятельности. К заданиям творческого характера можно отнести решение задач несколькими способами, составление задач и примеров самими учащимися, написание докладов, рефератов, математических сказок и сочинений. В 7 классе это могут быть такие задания: 1) Докажите неравенство: а) б) 2) Найдите наименьшее (или наибольшее) значение выражения. При каком значении переменных оно достигается? а) б) 3) Приведите пример неравенства, в котором левая часть будет равняться правой части. Особую роль уделяют умению самостоятельно работать с книгой. Начиная с 5 класса, знакомлю со структурой учебника, с приемами выделения определений, формулировок теорем, указываю расположение справочного материала на форзацах учебника, повторительного материала пройденного курса. Затем учу читать математическую книгу, выделять главное, делить текст пункта на смысловые части, находить в тексте ответ на поставленный вопрос, читать чертеж, составлять план ответа, организуя поиск различных доказательств теорем. Практикую и самостоятельное изучение нового материала. Самостоятельная работа может входить почти во все методы обучения, применяться на разных этапах процесса обучения, для достижения тех же целей, которые предусмотрены и на работах, выполняемых под руководством учителя. Естественно, что на разных этапах обучения самостоятельные работы используются для достижения различных целей: -на этапе осознания учебного материала самостоятельные работы направлены на понимание смысла и структуры изучаемых понятий, теорем; - на этапе формирования умений по применению полученных сведений самостоятельные работы направлены, прежде всего, на отработку правильности выполняемых действий; - на этапе формирования навыков они направлены уже на отработку быстроты выполняемых действий. Самостоятельные работы необходимы как для овладения знаниями, так и для осуществления учителем контроля за их усвоением.
Содержание и анализ опытно-экспериментальной работы В данном исследовании представлена система самостоятельных работ по теме «Формулы сокращенного умножения». Исследование проводилось в 7«А» и 7«Б» классах. Экспериментальным был 7«Б» класс, а контрольным - 7«А». Оба класса занимаются по программе, рекомендованной министерством образования, автором учебника «Алгебра» является Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов. В экспериментальном классе в ход урока мы включали разработанный нами комплекс упражнений по преобразованию математических и алгебраических выражений с помощью формул сокращенного умножения. Констатирующий эксперимент. Для определения уровня знаний, умений и навыков учащихся 7 класса в работе над математическими и алгебраическими выражениями было проведено диагностическое обследование. Контроль проводился в форме письменной проверочной работы. Цель данной работы: выявить имеющиеся знания и умения по преобразованию алгебраических выражений; определить пробелы в знаниях по данной теме. Учащимся предлагались задания на печатной основе. Детям необходимо было заполнить пропуски в предложенных выражениях, согласно требованию задания, вычислить значение выражения, упростить выражения. Задания располагались по принципу «от простого к сложному». Последнее, задание носило сложный характер и предполагалось для обязательного выполнения для получения оценки «отлично». Задание: 1. Вычислите: ü (-1)2; 43; (-6)3; 82. ü 0,52; 0,12; (-0,2)3; (-0,5)2. ü ü 2. Заполните таблицу: Таблица1.
3. Разложите выражение с помощью формул ü ü ü ü ü 4. Замените знаки * одночленами так, чтобы получились верные равенства: ü ü ü ü Каждое задание оценивалось определенным количеством баллов: первое задание – 6 баллов, второе задание – 9 баллов, третье задание – 12 баллов и четвертое – 15 баллов (максимум 42 балл). Критерии оценки: 5 – «отлично» - работа выполнена на 28 – 42 баллов; 4 – «хорошо» - работа выполнена на 16 – 27 баллов; 3 – «удовлетворительно» - работа выполнена на 9 – 15 баллов; 2 – «неудовлетворительно» - работа выполнена меньше, чем на 8 баллов. Уровни: Высокий уровень – 28 – 42 балла; Средний уровень – 16 – 27 баллов; Низкий уровень – меньше 15 баллов. В данной проверочной работе учитывались, при оценивании, знания и умения работать с выражениями, вычислительные ошибки исправлялись, на количество баллов и последующую оценку они тоже влияли. Причиной пробелов в знаниях мы видим в следующем: ü недостаточное количество упражнений по данной теме ü отсутствие систематичности заданий ü отсутствие упражнений, направленных на формирование навыков работы с выражениями. В результате проведенного исследования были получены следующие данные, которые представлены в табл. Таблица 2.
Отобразим полученные данные в виде рис. 1.
Рис.1 Из диаграммы видно, что в экспериментальном классе на начало эксперимента учащихся высокого уровня больше на 6,9%, чем в контрольном классе, учащихся среднего уровня больше на 3,4%, а учащихся низкого уровня меньше на 10,3%. Представим результаты констатирующего эксперимента по успеваемости в качестве диаграммы 2. Из диаграммы видно, что общая успеваемость у контрольного и экспериментального классов – 93,1%, а качественная успеваемость различна: у 7«А» (контрольного) класса она равна 69%, а у 7«Б» (экспериментального) класса – 79,3%.
Рис.2 Формирующий эксперимент Для устранения пробелов в знаниях и умениях учащихся по преобразованию алгебраических выражений нами была разработана система упражнений. Пропедевтическими упражнениями были: 1. Какие числа нужно вставить вместо пропусков, чтобы получить верные равенства: 52=….=…; (-6)2=…=…; 73=…=…; (-4)3=…=… 2. Заполни таблицу:
Рис. 3 Из гистограммы видно, что работу выполняли 10 учащихся. Из них первый уровень выбрали 2 человека, второй уровень – 4 человека, третий уровень – 4 человека. Все учащиеся справились с предложенной им работой: двое учащихся получили «5», пятеро – «4», трое - «3», не справившихся с работой учеников не было. Таким образом, каждый учащийся испытал успех и гордость за то, что смог самостоятельно решить работу и получил за это оценку. Многие из них уже на следующем уроке стали более активными, у них появилось желание работать и работать хорошо. Выводы по II главе Самостоятельная работа оказывает значительное влияние на глубину и прочность знаний учащихся по предмету, на развитие их познавательных способностей, на темп усвоения нового материала. Практический опыт учителей многих школ показал, что: 1. Систематически проводимая самостоятельная работа (с учебником по решению задач, выполнению наблюдений и опытов) при правильной ее организации способствует получению учащимися более глубоких и прочных знаний по сравнению с теми, которые они приобретают при сообщении учителем готовых знаний. 2. Организация выполнения учащимися разнообразных по дидактической цели и содержанию самостоятельных работ способствует развитию их познавательных и творческих способностей, развитию мышления. 3. При тщательно продуманной методике проведения самостоятельных работ ускоряются темпы формирования у учащихся умений и навыков практического характера, а это в свою очередь оказывает положительное влияние на формирование познавательных умений и навыков. 4. С течением времени при систематической организации самостоятельной работы на уроках и сочетании ее с различными видами домашней работы по предмету у учащихся вырабатываются устойчивые навыки самостоятельной работы. В результате для выполнения примерно одинаковых по объему и степени трудности работ учащиеся затрачивают значительно меньше времени по сравнению с учащимися таких классов, в которых самостоятельная работа совершенно не организуется или проводится нерегулярно. Это позволяет постепенно наращивать темпы изучения программного материала, увеличить время на решение задач, выполнение экспериментальных работ и других видов работ творческого характера. Заключение
В процессе рассмотрения данной проблемы выяснилось, что для эффективной организации самостоятельной работы школьника учитель должен уметь спланировать познавательный процесс учащегося и правильно выбрать способ решения задачи, при этом большое значение уделяется подборке учебного материала. Повышение качества обучения тесно связано с совершенствованием методики самостоятельной работы учащихся на уроке и внеурочное время. Для повышения качества обучения особое значение имеет развитие познавательного интереса школьников математике. Учащиеся должны понимать, каков смысл изучения предлагаемого материала. Более того, современные школьники вправе желать, чтобы самостоятельная деятельность была интересной, давала удовлетворение. Развитию самосто
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1823; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.225 (0.021 с.) |

 2x+…2; (2-x)2=22-2
2x+…2; (2-x)2=22-2  .
.
 ;
;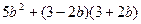 ;
;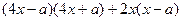 .
.








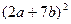 ; б)
; б) 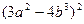
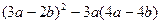

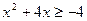 ;
; .
.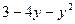 ;
; .
.