
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Технические нормативы проектируемого участка дорогиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В зависимостиот категории автомобильной дороги, интенсивности движения транспортных средств, типа подвижного состава по СНиПу 2.05.02-85 /2/ определяются технические нормативы для проектируемого участка дороги с последующим занесением полученных данных в таблицу. Форма таблицы приведена в примере. Подмостовые габариты для соответствующего класса реки устанавливаются по приложению 1. Пример. Определить технические нормативы автомобильной дороги II технической категории, на участке которой проектируется мостовой переход и установить подмостовые габариты для VII класса реки. В соответствии с требованиями СНиПа 2.05.02-85 /2/ автомобильная дорога II технической категории имеет технические нормативы, приведенные в (табл. 6). Таблица 6 Технические нормативы дороги II технической категории
По приложению 1 устанавливаются подмостовые габариты для VII класса реки /4/: - гарантированная глубина судоходного хода 0,7 м и менее; - ширина подмостового габарита неразрезного пролета 40/30 м; - высота подмостового габарита –7 м. 3. ГИДРОЛОГИЧЕСКИЕ РАСЧЁТЫ 3.1.Общие сведения о гидрологических расчетах Гидрологические расчеты включают в себя решение многих важных задач, такие как: определение максимального расхода Qр, установление характерных уровней воды в реке УМВ -уровня меженых вод, УВВ- уровня высоких вод, РСУ- расчетного судоходного уровня, построение уровенного графика, представляющего собой зависимость уровня воды в реке Z от времени t, т.е. Z=f(t), установление характеристик волнового режима реки и т.д. Но одной из основных задач гидрологических расчетов является определение максимального расхода расчетной вероятности превышения Qр и соответствующего ему расчетного уровня воды в реке Z. Расчет отверстия мостов невозможен без правильного определения расхода заданной вероятности превышения, так как от величины максимального расхода зависят основные размеры мостового перехода.
Мостовые переходы строятся на длительный эксплуатационный срок, порядка 50-100 лет, поэтому при их проектировании необходимо предусматривать возможность пропуска высоких вод редкой повторяемости. Технические условия /2/ при проектировании мостов на автомобильных дорогах, а также на городских дорогах и улицах, предусматривают следующие значения вероятности превышения паводка в зависимости от технической категории дороги: на дорогах I, II и III категорий - мостовые переходы рассчитываются на 1% вероятность превышения паводка, т.е. на максимальный расход, который будет наблюдаться один раз в 100 лет; на дорогах IV и V технических категорий мостовые переходы рассчитываются на 2% вероятность превышения паводка, т.е. на максимальный расход, который будет зарегистрирован один раз в 50 лет. В отношении гидрологической изученности все реки подразделяются на две группы. К первым относятся реки с водомерными постами, которые располагают многолетними наблюдениями за режимом реки (от 15 и более лет). Ко второй - реки, мало изученные имеющие менее 15 лет наблюдений за режимом реки, и совсем не изученные в гидрологическом отношении. В зависимости от степени гидрологической изученности рек, для определения величины максимальных паводковых расходов применяют один из двух существующих методов. Первый - метод математической статистики, базирующийся на теории вероятностей. Его используют для рек, которые имеют данные многолетних наблюдений за режимом реки. Второй метод включает в себя установление тех или иных эмпирических связей (аналогий). Метод аналогий применяют для рек, недостаточно изученных в гидрологическом отношении, и совсем не изученных. В этом случае максимальный расход расчетной вероятности превышения определяют по аналогии с другими реками, которые находятся в одинаковых физико-географических условиях и для которых имеются данные многолетних натурных наблюдений /3/.
3.2. Определение расчётного расхода водотока методом математической статистики Величина максимального расхода в реке зависит от множества факторов, не поддающихся точному прогнозированию на длительную перспективу во времени, таких как осадки, температура воздуха, испарение, направление и скорость ветра ит.д. В различные годы на одной и той же реке метеорологические условия складываются неодинаково и максимальные расходы из-за этого меняются из года в год, от очень больших до малых значений. По этой причине максимальные расходы рек относят к гидрологическим величинам, колебания значений которых имеют случайный характер. Однако в изменении максимальных расходов имеется некоторая закономерность. Она заключается в том, что среднее значение максимальных расходов для данного створа реки является практически постоянным, не зависящим от продолжительности наблюдений. Это дает возможность применять для определения расчетного расхода метод математической статистики, который основан на теории вероятности. Вести обработку ряда максимальных расходов методом математической статистики возможно в том случае, если число лет натурных наблюдений не менее 15. Этот метод используется для определения расчетного расхода с З0-х годов прошлого века по предложению Е. В. Болдакова. При определении расчетного расхода водотока устанавливается расчетная вероятность превышения (Р,%) в зависимости от технической категории автомобильной дороги по табл.7 Расчётный расход заданной вероятности превышения определяется с помощью клетчатки вероятности нормального распределения (приложение 2). Для этого, используя данные водомерного поста, составляется ряд годовых максимальных расходов Qi; и соответствующих им уровней воды Z в порядке убывания (табл.8).
Таблица 7 Определение расчетной вероятности превышения
Таблица 8 К определению расчетного расхода водотока в створе мостового перехода
Расчет выполняется в следующей последовательности. 1. Находят среднее арифметическое значение ряда
где åQi -суммарный расход водотока за n лет, м /с; n -число лет наблюдений.
2. Вычисляют модульные коэффициенты для каждого года наблюдений и заполняют графу 5 в табл. 8, а затем графы 6,7,8
Контролем вычислений являются два условия:
3. Подсчитывают коэффициент вариации ряда СV, который характеризуется отношением среднеквадратического отклонения δ всех максимальных расходов Qi к средней арифметической величине Qо, т.е. δ/Qo
В практических расчетах коэффициент вариации вычисляется по формуле
Если число лет наблюдений ≥30, то в расчетную формулу (3) вместо n-1 вводится параметр n. 4. Определяют эмпирическую вероятность превышения Pi в процентах фактических модульных коэффициентов для каждого года наблюдений, по формуле Н. Н. Чегодаева
где m - порядковый номер члена данного ряда при расположении членов в убывающем порядке; n - число лет наблюдений. Результаты заносят в графу 9 табл.8 5. По данным таблицы 8 (графы 5 и 9) на клетчатке вероятностей нормального распределения (приложение 2) строят эмпирическую кривую распределения для данного ряда наблюдений (рис. 3) На эту же клетчатку вероятностей наносятся три теоретические интегральные кривые распределения С. Н. Крицкого и M. Ф. Менкеля для подсчитанного значения коэффициента вариации СV и заданных отношений:
где Cs -коэффициент асимметрии Ординаты для построения теоретических интегральных кривых распределения даются в приложениях 3, 4, 5. Если подсчитанное значение коэффициента вариации СV по формуле (3) не совпадает со значением СV, которые даны в приложениях 3, 4 и 5, то значения ординаты К следует определять путем интерполяции. За расчетную кривую на клетчатке вероятностей принимают ту теоретическую интегральную кривую распределения, которая наилучшим образом совпадает с эмпирической, построенной по данным табл. 8 (графы 5 и 9).По этой расчетной теоретической интегральной кривой распределения в зависимости от принятой эмпирической вероятности превышения Р (табл.7) определяют значение расчетного модульного коэффициента Кр 6. Определяют расчетный расход водотока QР, м3/c по формуле:
где Кр- расчетный модульный коэффициент; Qo- среднее арифметическое значение, м3/c. Пример. Определить расчетный расход р. Сок в створе проектируемого мостового перехода. Исходные данные: автомобильная дорога II технической категории; ряд годовых максимальных уровней воды zi; и расходов Qi, значения которых приведены в табл.9. Таблица 9
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.215 (0.012 с.) |

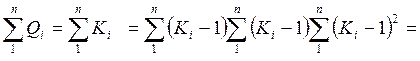
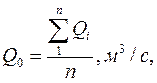 (1)
(1)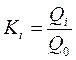 (2)
(2)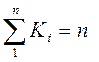
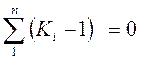
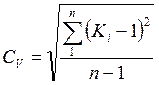 (3)
(3)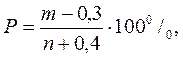 (4)
(4)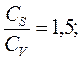
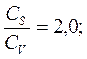
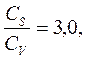
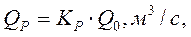 (5)
(5)


