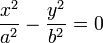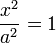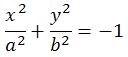Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенство Коши-Буняковского.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Неравенство Коши-Буняковского. Скалярным произведением векторов х,у принадлеж. R n: x=(x1,…,xn), y=(y1,…yn) называется число (х,у)= Для любых двух векторов а и b в евклидовом пространстве справедливо неравенство
Доказательство: Возьмем произвольное число t и составим вектор Тогда Легко заметить квадратный трехчлен, если
Квадратный трехчлен D= β2- α γ≤ 0, подставим обратно выражения в неравенство:
Т.о., нер-во Коши-Буняковского равносильно неравенству
Неравенство треугольника. Для любых двух векторов а и b в евклидовом пространстве справедливо соотношение, называемое неравенством треугольника:
В силу неравенства Коши-Буняковского, согласно которому
Извлечем корень из обеих частей этого неравенства без потери знака, т.к. обе части заведомо положительны. Получим:
Линейная независимость лестничной системы векторов. Предложение: любая лестничная система векторов линейно независима. Доказательство: Предположим противное. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть, например, а линейно выражается через b, c, …, то есть
Но такое равенство невозможно, поскольку первая координата вектора а отлична от нуля, а первая координата вектора Полученное противоречие доказывает, что линейная система векторов линейно независима.
4. Однозначность разложения вектора по базису. Предложение: Координаты вектора в данном базисе определены однозначно. Допустим,что существуют два способа разложения вектора а по базису Тогда И Если вычесть эти два равенства, получим, что
Так как векторы базиса линейно независимы, то они не равны нулю. Значит, То есть k=l, и существует лишь один способ разложения вектора по базису.
Формула умножения комплексных чисел в тригонометрической форме. Возьмем два комплексных числа в тригонометрической форме.
получим для наших двух комплексных чисел формулу:
=
Т.о., для умножения z1 на z2 модули этих чисел следует перемножить, а аргументы сложить.
Формула деления комплексных чисел в тригонометрической форме Возьмем два комплексных числа в тригонометрической форме.
Используя формулу деления комплексных чисел вида
получим для наших двух комплексных чисел формулу:
/учитывая основное тригонометрическое тождество, согласно которому = ( /используя тригонометрические свойства косинуса и синуса суммы и разности/ =
Таким образом, для нахождения частного z1/z2 следует модуль числа z1 разделить на модуль числа z2, а из аргумента числа z1 вычесть аргумент числа z2
Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений.
Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение. Запишем общий вид однородной системы m уравнений с n неизвестными:
а21х1+ а22х2+…+ а2nхn=0 … аm1х1+ аm2х2+…+ аmnхn=0, где n>m Применим к системе метод Гаусса. В процессе преобразований не могут получиться противоречивые уравнения
т.к. все свободные члены уравнений – нули. Значит, после некоторого числа шагов мы получаем систему, где каждому уравнению будет соответствовать свое базисное неизвестное. Но поскольку число уравнений меньше числа неизвестных, то и число базисных неизвестных должно быть меньше числа неизвестных. Следовательно, обязательно имеются свободные неизвестные, а система имеет бесчисленное множество решений.
Формулы для вычисления координат вектора в ортогональном базисе.
Кривые 2 порядка
Уравнение эллипса (рис.1):
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ (рис.1), при a < b фокусы эллипса лежат на оси ОY, а при a = b эллипс становится окружностью (фокусы эллипса в этом случае совпадают с центром окружности). Таким образом, окружность есть частный случай эллипса.
Отрезок F1F2 = 2 с, где, называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осью эллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.
Простейшее уравнение гиперболы
Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы.
Если 2c - расстояние между фокусами гиперболы, то между a, b и c существует соотношение
a2 + b2 = c2.
При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид
x2 - y2 = a2.
Фокусы гиперболы лежат на ее действительной оси.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.
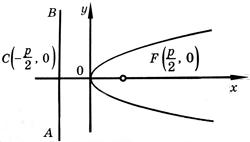
Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.
Простейшее уравнение параболы
y2 = 2px. (*)
Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.
Координаты фокуса F параболы
Эксцентриситет параболы e = 1.
y2 = 2px (p > 0)
Две пересекающиеся прямые
Две параллельные прямые
Двукратная(одна) прямая x2 = 0 Мнимые параллельные прямые
Мнимый эллипс
Неравенство Коши-Буняковского. Скалярным произведением векторов х,у принадлеж. R n: x=(x1,…,xn), y=(y1,…yn) называется число (х,у)= Для любых двух векторов а и b в евклидовом пространстве справедливо неравенство
Доказательство: Возьмем произвольное число t и составим вектор Тогда Легко заметить квадратный трехчлен, если
Квадратный трехчлен D= β2- α γ≤ 0, подставим обратно выражения в неравенство:
Т.о., нер-во Коши-Буняковского равносильно неравенству
Неравенство треугольника. Для любых двух векторов а и b в евклидовом пространстве справедливо соотношение, называемое неравенством треугольника:
В силу неравенства Коши-Буняковского, согласно которому
Извлечем корень из обеих частей этого неравенства без потери знака, т.к. обе части заведомо положительны. Получим:
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |



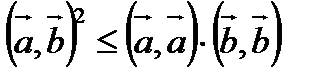

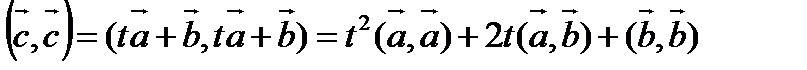
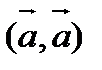 =α,
=α,  =β, а
=β, а  =γ, т.е.
=γ, т.е.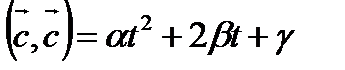
 при любом значении t неотрицателен, поскольку
при любом значении t неотрицателен, поскольку 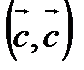 ≥0, следовательно, дискриминант данного трехчлена неположителен.
≥0, следовательно, дискриминант данного трехчлена неположителен. -
- 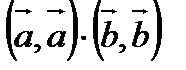 ≤0, или
≤0, или  , чтд.
, чтд.

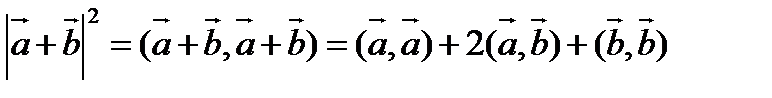
 ,
,
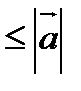 2+2
2+2 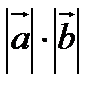 +
+  2=(
2=( +
+  )2
)2
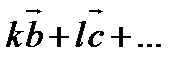 равна нулю (из определения лестничной системы векторов первая координата всех последующих векторов равна нулю).
равна нулю (из определения лестничной системы векторов первая координата всех последующих векторов равна нулю).



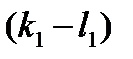 =0,
=0, 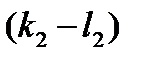 =0, …,
=0, …, 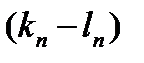 =0
=0


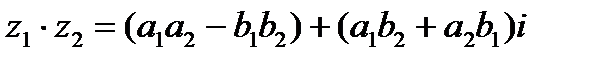 ,
, = /используя тригонометрические формулы косинуса и синуса суммы/
= /используя тригонометрические формулы косинуса и синуса суммы/
 ,
,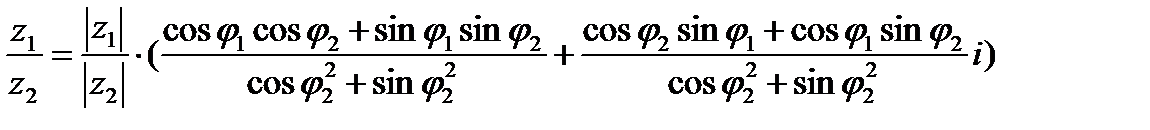 =
=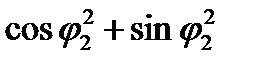 =1/
=1/ )+ (
)+ (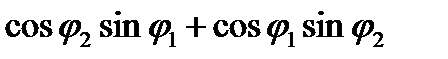 ) i =
) i =
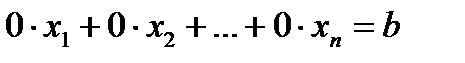 , где b ≠0,
, где b ≠0,
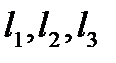 - ортогональный базис
- ортогональный базис






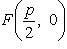 (*). (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)
(*). (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)