
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування задач з теми, зокрема і поглибленого рівня.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 1. Дано АВСD– трапеція (ВС║АD) A B C ВС=6см, АD=14см. M N MN – серед.лінія, АС – діаг. Знайти MN -? МТ-? TN -? B D Розв’язок 1) MN = 6+14=10 (см). 2) ΔАВС, МТ ║ВС, М – серед. АВ, то За теоремою Фалеса Т – серед АС. Отже МТ – середня лінія ΔАВС, МТ = ½ВС = 3 (см). 3) ΔACD, аналогично TN = ½AD =7 (см). Відповідь. 10 см,3 см, 7см. Задача 2. Бісектриси кутів при основі трапеції перетинаються на її другій основі. Доведіть, що друга основа дорівнює сумі бічних сторін трапеції. Доведення
Розв'язання Нехай ABCD (рис. 2) — дана трапеція (AD || BC), AB = CD = 4см, ВС = 10 см, BC < AD, Відповідь: 12 см. Задача 4. Сторона трикутника дорівнює 10 см, а одна із середніх ліній — 6 см. Знайдіть дві інші сторони трикутника, якщо периметр даного трикутника дорівнює 30 см. Розв’язання За теоремою про середню лінію трикутника одержуємо, що сторона, яка лежить проти даної середньої лінії, дорівнює 12 см, тоді третя сторона трикутника: 30 – (10 + 12) = 8 см. Відповідь: 8 см. Задача 5. Основи трапеції дорівнюють 6 см і 20 см. Знайдіть довжину відрізка, який сполучає середини діагоналей трапеції.
Нехай ABCD (рис. 3) — дана трапеція з основами AD = 20 см і ВС = 10 см, точки М і N — середини діагоналей АС і BD відповідно. У трикутнику ACD проведемо середню лінію MF, паралельну AD. Оскільки точка М — середина АС, то за теоремою Фалеса точка M — середина BD. Тоді MN належить MF. MF = Відповідь: 7 см. Задача 6. Основи трапеції дорівнюють а і b. Визначте довжину відрізків, на які ділить більшу основу пряма, що проходить через середину однієї з бічних сторін паралельно другій бічній стороні трапеції.
Розв'язання
Відповідь: Задача 7. Основи рівнобічної трапеції дорівнюють Розв’язання 1) Нехай дано трапецію
2) Розглянемо
Тому Тоді 3) Аналогічно Тому
Звідки 4) Прирівнявши знайдені нами значення
5) Розглянемо відношення
Отже 6) Підставивши отримані значення, маємо:
Відповідь. Задача 8 Довести, що в рівнобічній трапеції, діагональ розбиває трапецію на 4 трикутника з яких два прилеглі до основ, рівнобедрені, а два прилеглі до бічних сторін, рівні між собою. Доведення 1) Нехай діагоналі трапеції 2)
3) Оскільки
Оскільки
звідки
Добірка задач для проведення самостійних, контрольних робіт. Самостійна робота Варіант І 1. Знайдіть периметр трикутника, якщо його середні лінії дорівнюють 6 см, 9 см і 10 см. (Відповідь: 50 см.) 2. У рівнобедреній трапеції ABCD основи AD і ВС дорівнюють відповідно 17 см і 5 см. З вершини В проведено висоту BE. Знайдіть довжину відрізка АЕ. (Відповідь: 6 см.) 3. Діагональ рівнобедреної трапеції утворює з основою кут 28°, а бічна сторона дорівнює меншій основі. Знайдіть кути трапеції. (Відповідь: 56°, 56°, 124°, 124°.) 4. У трапеції ABCD основа AD більша від основи ВС на 6 см, а середня лінія дорівнює 7 см. Знайдіть довжини відрізків, на які діагональ АС ділить середню лінію. (Відповідь: 2 см, 5 см.) 5. У трикутнику ABC сторону АВ розділено на три рівні частини і через точки розподілу проведено прямі, паралельні стороні АС. Знайдіть довжини відрізків цих прямих, розташованих між сторонами АВ і ВС трикутника, якщо АС = 9 см. (Відповідь: 3 см і б см.)
Варіант II 1. Сторони трикутника дорівнюють 10 см, 12 см і 14 см. Знайдіть периметр трикутника, вершини якого — середини сторін даного трикутника. (Відповідь: 18 см.) 2. У рівнобедреній трапеції ABCD висота ВК ділить основу AD на відрізки АК = 4 см і KD = 10 см. Знайдіть основу ВС трапеції. (Відповідь: 6 см.) 3. Діагональ рівнобедреної трапеції утворює з основою кут 54°, а її бічна сторона дорівнює більшій основі. Знайдіть кути трапеції. (Відповідь: 72°, 72°, 108°, 108°.) 4. У трапеції ABCD середня лінія EF перетинає діагональ АС у точці К. Різниця відрізків KF і КЕ дорівнює 3 см. Знайдіть основи трапеції, якщо їх сума дорівнює 18 см. (Відповідь: 6 см, 12 см.) 5. У трикутнику ABC сторону АС розділено на три рівних відрізки і через точки розподілу проведено прямі, паралельні стороні АВ трикутника. Менший із відрізків цих прямих, розташованих між сторонами трикутника, менший за сторону АВ на 8 см. Знайдіть сторону АВ трикутника. (Відповідь: 12 см.)
Самостійна робота Варіант І 1). Діагональ рівнобедреної трапеції утворює з основою кут 32°, а її бічна сторона дорівнює меншій основі. Знайдіть кути трапеції.
2). Більша основа рівнобедреної трапеції дорівнює 18 см, а її діагональ є бісектрисою гострого кута трапеції. Знайдіть меншу основу трапеції, якщо її периметр дорівнює 54 см.
Варіант II 1). У рівнобедреній трапеції діагональ дорівнює більшій основі та утворює з нею кут 38°. Знайдіть кути трапеції. 2). У рівнобедреній трапеції діагональ є бісектрисою кута при основі. Більша основа трапеції дорівнює 26 см, а периметр — 50 см. Знайдіть меншу основу трапеції.
Контрольна робота Кожне правильно розв'язане завдання початкового та середнього рівнів оцінюється в 1 бал, достатнього рівня — в 1,5 бала, високого рівня — в 3 бали. Варіант І Початковий рівень У завданнях 1—3 заповніть пропуски в тексті. 1. Якщо паралельні прямі, які пересікають сторони кута, відтинають на одній його стороні ______ відрізки, то вони відтинають __________ відрізки й на __________ його стороні. 2. Відрізок, що сполучає ________ двох сторін трикутника, називається _______________________________ трикутника. 3. Середня лінія трапеції ________________ основам і дорівнює _________ _______________. Середній рівень У завданнях 4—6 виберіть правильну відповідь. 4. Якщо ABCD — трапеція, AD || BC, a) AB = CD; б) 5. Якщо MN — середня лінія трикутника ABC, точка М — серединна АС, точка N — середина АВ і MN + BC = 15см, то: а) ВС = 8см; б) ВС = 9см; в) ВС = 10 см. 6. У трапеції ABCD AB || DC, MN — середня лінія трапеції, точка М — середина AD, точка N — середина ВС. Чому дорівнює сторона DC, якщо АВ = 20 см, MN = 24 см? а) 28 см; б) 30 см; в) 26 см. Достатній рівень 7. Основи трапеції відносяться як 5: 6, а їх різниця дорівнює 6 см. Знайдіть середню лінію трапеції. 8. Знайдіть кути рівнобічної трапеції, якщо різниця двох її кутів дорівнює 50°. Високий рівень 9. Основи прямокутної трапеції дорівнюють 8 см і 14 см, а один з її кутів дорівнює 135°. Знайдіть меншу бічну сторону трапеції.
Варіант II Початковий рівень У завданнях 1—3 заповніть пропуски в тексті. 1. Трапецією називається __________, у якого тільки дві протилежні сторони _____________. 2. Середня лінія трикутника, що сполучає ____________ двох його сторін, _____________ третій стороні та дорівнює ________________. 3. Паралельні прямі, які перетинають дві дані прямі та відсікають _______ рівні відрізки, відсікають ___________ і на іншій прямій.
У завданнях 4—6 виберіть правильну відповідь. 4. Якщо нарисі А 1 В 1 || А 2 В 2 || А 3 В 3і А 1 А 2 = А 2 А 3, то: а) А 1 А 2 = А 1 В 1; б) В 1 В 2 = А 1 В 1; в) B 1 B 2 = B 2 B 3. 5. Якщо ABCD — трапеція (АВ || CD), a) 6. Чому дорівнює середня лінія трапеції ABCD, якщо ВС = 5см, AD = 7 см? а) 2,5 см; б) 3,5 см; в) 6 см. Достатній рівень 7. Основи трапеції відносяться як 3: 4, а її середня лінія дорівнює 14 см. Знайдіть основи трапеції. 8. Знайдіть кути рівнобічної трапеції, якщо сума двох її кутів дорівнює 100°. Високий рівень 9. У рівнобічній трапеції з гострим кутом 60° сума основ дорівнює 86 см, а бічна сторона — 22 см. Знайдіть основи трапеції.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 5095; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.254 (0.012 с.) |

 Нехай ABCD (рис. 1) — дана трапеція (ВС || AD), AK — бісектриса кута BAD. Отже,
Нехай ABCD (рис. 1) — дана трапеція (ВС || AD), AK — бісектриса кута BAD. Отже,  BAK =
BAK = 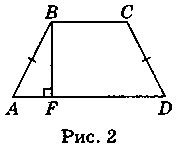 Задача 3. У рівнобічній трапеції менша основа дорівнює 10 см, бічна сторона — 4 см, а кут між бічною стороною та більшою основою дорівнює 60°. Знайдіть середню лінію трапеції.
Задача 3. У рівнобічній трапеції менша основа дорівнює 10 см, бічна сторона — 4 см, а кут між бічною стороною та більшою основою дорівнює 60°. Знайдіть середню лінію трапеції. AD). У трикутнику ABF
AD). У трикутнику ABF 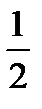 АВ = 2 см. Оскільки AD = BC + + 2 AF, то AD = 10 + 4 = 14 см. Отже, середня лінія цієї трапеції (14 + 10): 2 = 12 см.
АВ = 2 см. Оскільки AD = BC + + 2 AF, то AD = 10 + 4 = 14 см. Отже, середня лінія цієї трапеції (14 + 10): 2 = 12 см. Розв'язання
Розв'язання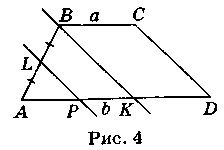 Нехай ABCD (рис. 4) — дана трапеція, у якій AD || ВС, AD = b, ВС = а. Точка L — середина АВ, LP || CD. Проведемо пряму ВК, паралельну стороні CD. Отже, LP || ВК. Оскільки точка L — середина АВ, то за теоремою Фалеса АР = = РК. Оскільки ВК || CD, ВС || KD, то чотирикутник KBCD — паралелограм і KD = ВС = а. Звідси АР =
Нехай ABCD (рис. 4) — дана трапеція, у якій AD || ВС, AD = b, ВС = а. Точка L — середина АВ, LP || CD. Проведемо пряму ВК, паралельну стороні CD. Отже, LP || ВК. Оскільки точка L — середина АВ, то за теоремою Фалеса АР = = РК. Оскільки ВК || CD, ВС || KD, то чотирикутник KBCD — паралелограм і KD = ВС = а. Звідси АР =  , PD =
, PD =  .
. ;
;  .
. і
і  (
(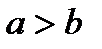 ). Прямі, які з’єднують середину більшої основи з кінцями меншої основи, переринають діагоналі трапеції в точка
). Прямі, які з’єднують середину більшої основи з кінцями меншої основи, переринають діагоналі трапеції в точка  і
і  . Знайти довжину відрізка
. Знайти довжину відрізка 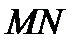 .
. ,
, 
 ;
;




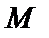


 ;
; ,
, (чому?).
(чому?). та
та 

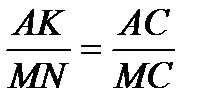 ,
,
 ,
, ,
,
 маємо:
маємо: ,
, ,
,
 ,
, ,
, ,
,
 .
. .
.
 перетинаються в точці
перетинаються в точці  .
. (рівні висоти і основи)
(рівні висоти і основи)




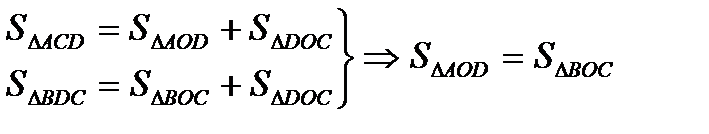
 – рівнобічна трапеція,
– рівнобічна трапеція, ,
,  .
. ,
,  ,
, .
.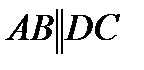 ,
,
 – рівнобедрені(кути при основі рівні).
– рівнобедрені(кути при основі рівні). Середній рівень
Середній рівень


