Максимизация прибыли монопольными фирмами в долгосрочном периоде

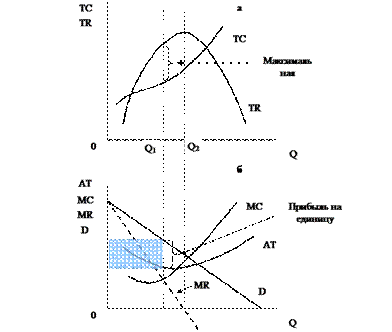
Если к кривым спроса и предельного дохода добавить кривые издержек предприятия-монополиста, можно выявить такую комбинацию «цена-количество», которая принесет максимальную прибыль. Это можно сделать, либо сравнивая совокупные издержки с совокупным доходом, либо с помощью предельного подхода (см. рис. 7.3).

В первом случае (рис. 7.3 а) совокупная прибыль равна величине вертикального разрыва между кривыми совокупного дохода и совокупных издержек. Как видим, максимум прибыли и максимум дохода достигаются при разных уровнях выпуска продукции. В интервале между Q₁ и Q₂ TR продолжает расти, но совокупные издержки растут еще быстрее, и прибыль падает.

На рисунке 7.3 б представлен предельный подход. В краткосрочном периоде монополист максимизирует прибыль, производя такое количество продукции, при котором MC = MR, поскольку пока предельный доход (MR) превышает предельные издержки (MC), увеличение выпуска на единицу увеличивает совокупный доход в большей степени, чем совокупные издержки, и, тем самым, увеличивает совокупную прибыль. А когда MR становится меньше MC, любое дальнейшее увеличение выпуска продукции ведет к уменьшению совокупной прибыли.

Рис. 7.3 – Максимизация прибыли предприятия-монополиста

 

Графически объем выпуска, дающего максимальную прибыль, находится в точке, где восходящая ветвь кривой предельных издержек пересекает кривую предельного дохода. Прибыль, приходящаяся на единицу продукции при этом объеме, равна вертикальному разрыву между кривой спроса (она указывает на цену, по которой продается продукция) и кривой ATC. Совокупная прибыль равна прибыли на единицу, умноженной на объем выпуска (площадь заштрихованного прямоугольника).

Если рыночные условия неблагоприятны, то монополия может оказаться не в состоянии получать прибыль в пределах краткосрочного периода. Если спрос недостаточен для получения прибыли (кривая спроса лежит ниже кривой средних совокупных издержек), то предприятие-монополист минимизирует убытки, производя продукцию в объеме, соответствующем пересечению кривых MR и MC. Если же предприятие не сможет из-за падения цены компенсировать даже средние переменные издержки (кривая спроса лежит ниже кривой средних переменных издержек), то единственный вариант краткосрочной стратегии минимизации убытков – приостановка производства.

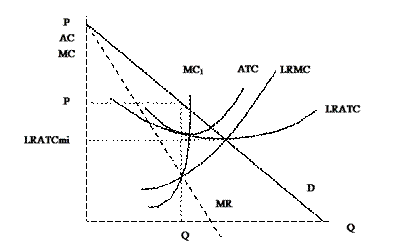
В долгосрочном плане максимизирующая прибыль монополия расширяет свои операции до тех пор, пока не выпускается количество товара, соответствующее равенству предельного дохода и долгосрочных предельных издержек (MR = LRMC).

На рисунке 7.4 представлен случай, когда предприятие строит завод меньшего размера, чем тот, который соответствует LRATCmin. Так происходит, когда уровень спроса на продукт монополиста таков, что кривая MR пересекается с кривой LRMC в точке, где LRMC < LRATC.

Рис. 7.4 – Монополия, не достигающая всей экономии от масштаба производства

При таком уровне спроса монополии не удается использовать всю экономию от масштаба производства (LRATC при объеме выпуска Q больше, чем LRATCmin).

На рисунке 7.5 показан такой уровень спроса, при котором MR = LRMC в точке, где LRMC = LRATC.

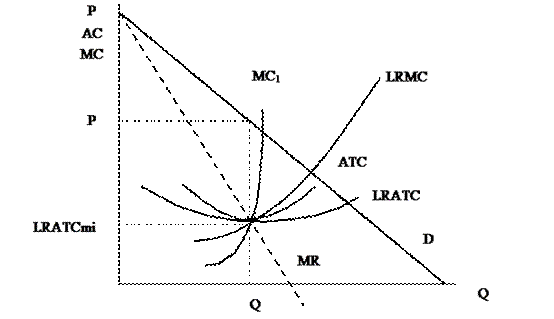
Рис. 7.5 – Долгосрочное равновесие

 

В этом случае монополия строит завод размером, соответствующим LRATCmin и добивается использования всей возможной в долгосрочном плане экономии от масштаба производства.

Однако монопольная цена P превышает LRATCmin и LRMC, следовательно, потребители не получают всех преимуществ от низких средних издержек монополиста, так как монополист из-за отсутствия конкуренции может назначить цену выше LRATCmin.

В случае, когда спрос на продукт монополиста таков, что кривая MR пересекает кривую LRMC, соответствующую осуществлению производства на единственном заводе, в точке, где LRMC > LRATC, монополия предпочтет построить два или более заводов, чтобы иметь возможность заработать более высокие прибыли.