
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні статистичні характеристики вибіркиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте У математичній статистиці вивчають числові характеристики вибірок, які узагальнюють об'єкти вибірки за певною ознакою. У разі обчислення статистичних характеристик вибіркою найчастіше називають набір значень певного параметра вибраних об'єктів, наприклад набір річних оцінок учнів з математики. Кожен елемент вибірки в цьому випадку називають варіантою. До основних числових характеристик належать: § середнє значення, § стандартне відхилення, асиметрія,ексцес. § медіана, § мода (показники центру вибірки), § варіаційний розмах вибірки (показники варіації) § дисперсія,середнє квадратичне відхилення. § кореляційний і регресійний аналіз. § нормальний закон розподілу § гістограма Вибіркове середнє значення — характеристика положення для вибіркового розподілу Середнє арифметичне декількох чисел — це відношення суми всіх чисел до їх кількості. Вибірковим середнім називається середнє арифметичне елементів даної вибірки:
Коли у вибірці є частоти значень ознаки або обчислення виконуються для інтервального варіаційного ряду, тоді варто визначити: xi – середнє значення ознаки ξ в i -му інтервалі, n i – частоту значень ознаки в i -му інтервалі. Тоді розрахункова формула набуде вигляду:
Середнє квадратичне відхилення — у теорії ймовірності і статистиці найпоширеніший показник розсіювання значень випадкової величини відносно її математичного сподівання. Вимірюється в одиницях виміру самої випадкової величини. Дисперсія (англ. Variance) є мірою відхилення значень випадкової величини від центру розподілу. Більші значення дисперсії свідчать про більші відхилення значень випадкової величини від центру розподілу Стандартне відхилення а — це параметр, який характеризує ступінь розкиду елементів вибірки відносно середнього значення:
де п — об'єм вибірки, х1 х2, хп — варіанти, х — середнє значення вибірки. Коефіцієнт варіації — відносна величина, що служить для характеристики коливання (мінливості) ознаки. Являє собою відношення середнього квадратичного відхилення τ до середнього арифметичного Х, виражається у відсотках: ν = τ/Х. Коефіцієнт варіації застосовується тоді, коли необхідно оцінити мінливість ознак об'єкта, які виражені в різних одиницях вимірювання. Варіювання вважається слабким, якщо ν<10%, якщо ν від 11-25%, то середнім і значним при ν>25%. Асиметрія — відсутність або порушення симетрії. Коефіцієнт асиметрії – характеризує ступінь несиметричності розподілу відносно середнього. Додатна асиметрія вказує на відхилення розподілу в бік додатних значень, від’ємна асиметрія вказує на відхилення розподілу в бік від’ємних значень.
Ексцесом теоретичного розподілу називають характеристику, що обчислюється за наступною формулою:
Коефіцієнт ексцесу - характеризує відносну гостроту або згладженість розподілу порівняно з нормальним розподілом. Додатній ексцес означає відносно гострокінцевий розподіл, від’ємний – відносно згладжений розподіл
Медіана — в статистиці це величина ознаки, що розташована по середині ранжованого ряду вибірки, тобто — це величина, що розташована в середині ряду величин, розташованих у зростаючому або спадному порядку; в теорії ймовірності — характеристика розподілення випадкової величини. Медіана ділить ряд значень ознаки на дві рівні частини, по обидві частини від неї розміщується однакова кількість одиниць сукупності.[1] Медіана є квантилем порядку 1/2. Позначається як Мода – те з даних, яке зустрічається в переліку даних найчастіше. Іншими словами, мода є найпоширеніше значення випадкової величини (ознаки). У дискретному ряду вона визначається візуально за найбільшою частотою (часткою), а в інтервальному — таким чином визначається модальний інтервал, а конкретне модальне значення розраховується за формулою:
де х0 та h — нижня межа та ширина модального інтервалу, fmo, fmo-1, fmo+1 — частоти (частки) відповідно модального, передмодального та післямодального інтервалів. Варіаційних розмах (інтервал, амплітуда) — це різниця між максимальним та мінімальним значеннями елементів вибірки Кореляцією називається неповний зв'язок між досліджуваними явищами. Це така залежність, коли будь - якому значенню однієї змінної величини може відповідати декілька різноманітних значень іншої змінної. Вона відображає закон множини причин і наслідків і є вільною неповною залежністю. Кореляційний аналіз є свого роду логічним продовженням (розвитком) методу статистичних групувань, його поглибленням. Він допомогає вирішити цілий ряд нових завдань у економічному аналізі. Розрахунки на основі кореляційних моделей підвищують ступінь точності аналізу, часто виявляють недоліки попереднього аналізу Головні завдання кореляційного аналізу: 1) оцінка за вибірковими даними коефіцієнт кореляції, перевірка значущості вибіркових коефіцієнтів кореляції або кореляційного відношення 2) оцінка близькості виявленого зв'язку до лінійного. 3) побудова довірчого інтервалу для коефіцієнтів кореляції.
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.007 с.) |

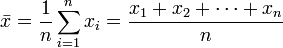 . (1.1)
. (1.1)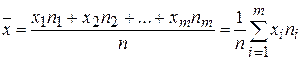 (1.2)
(1.2)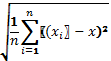 (1.3)
(1.3)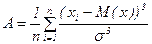 (1.4)
(1.4)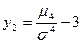 (1.5)
(1.5)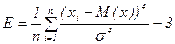 (1.6)
(1.6)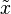 або
або 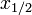 .
.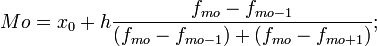 (1.7)
(1.7)


