
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение прямой геодезической задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задание состоит из двух задач, при решении которых следует руководствоваться указаниями к темам 3, 2 и 7.
Задача 1. Вычислить дирекционные углы линий ВС и CD, если известны дирекционный угол αАВ линии АВ и измеренные правые по ходу углы β1 и β2 (рис. 1). Рис. 1. К вычислению дирекционных углов сторон теодолитного хода. Исходный дирекционный угол αАВ берется в соответствии с шифром и фамилией студента: число градусов равно двузначному числу, состоящему из двух последних цифр шифра; число минут равно 30,2' плюс столько минут, сколько букв в фамилии студента. Пример.
Дирекционные углы вычисляют по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус горизонтальный угол, справа по ходу лежащий: αВC = αАВ + 180° - β1; αCD = αBC + 180° - β2. Примечание. Если при вычислении уменьшаемое окажется меньше вычитаемого, то к уменьшаемому прибавляют 360°. Если дирекционный угол получается больше 360°, то из него вычитают 360°. Задача 2. Найти координаты хс и ус точки С (рис. 1), если известны координаты хВ и уВ в точки В, длина (горизонтальное проложение) dВС линии ВС и дирекционный угол αBC этой линии. Координаты точки В и длина dВС берутся одинаковыми для всех вариантов: хВ = -14,02 м, уВ = +627,98 м, dВС = 239.14 м. Дирекционный угол αBC линии ВС следует взять из решения предыдущей задачи. Координаты точки С вычисляются по формулам:
где
Вычисления приращений координат рекомендуется вести на микрокалькуляторе либо по специальным таблицам [3]. Во втором случае для удобства вычислений дирекционный угол следует предварительно перевести в румб, пользуясь таблицей 1. Таблица 1. - Перевод дирекционных углов в румбы
В этом случае:
При вычислении приращений координат значения румбов следует округлить до целых минут. Знаки приращений определяют в зависимости от названия румба (табл. 2).
Таблица 2. – Знаки приращений прямоугольных координат
Пример: Вычислить приращения координат, если дано: dВС = 239,14 м; αВC = 19°35,0'. В соответствии с табл. 1 румб линии ВС гВС = СВ: 19°35,0'. Выполнив вычисления на микрокалькуляторе и определив знаки приращений по названию румба СВ, получаем Координаты точки С получаем алгебраическим сложением координат точки В с приращениями по линии ВС. Пример: Вычисление координат точки С выполняем по схеме
Задачи решают в специальной тетради; решение каждой из них должно сопровождаться схематическим чертежом, соответствующим выполняемому варианту. В задаче 1 пример подобран так, что вычисленный дирекционный угол αCD последней линии должен получиться на 1°10,0' больше, чем исходный дирекционный угол αАВ. Это может служить контролем правильности решения первой задачи. Решение задачи 2 непосредственно не контролируется. К ее решению надо подойти особенно внимательно, так как вычисленные координаты Задание 3. Составление топографического плана строительной площадки СОДЕРЖАНИЕ РАБОТЫ По данным полевых измерений составить и вычертить топографический план строительной площадки в масштабе 1:2000 с высотой сечения рельефа 1м.
Рис. 2. Схема теодолитно-высотного хода съемочного обоснования Работа состоит из следующих этапов: - обработка ведомости вычисления координат вершин теодолитного хода; - обработка тахеометрического журнала; - построение топографического плана. ИСХОДНЫЕ ДАННЫЕ 1. Для съемки участка на местности между двумя пунктами полигонометрия ПЗ 8 и ПЗ 19 был проложен теодолитно-высотный ход. В нем измерены длины всех сторон (рис. 2), а на каждой вершине хода - правый по ходу горизонтальный угол и углы наклона на предыдущую и последующую вершины. Результаты измерений горизонтальных углов в линий (табл. 3), а также тригонометрического нивелирования (табл. 5 в 5а) являются общими для всех вариантов. Измерение углов производилось оптическим теодолитом 2ТЗО с точностью отсчетов но шкаловому микроскопу 0,5'. 2. Известны координаты полигонометрических знаков ПЗ 8 и ПЗ 19 (т. е. начальной и конечной точек хода):
Таблица 3. – Результаты измерений углов и длин сторон хода
Известны также исходный α0 и конечный αn дирекционные углы: α0 -дирекционный угол направления ПЗ 7—ПЗ 8; берется в соответствии с шифром и фамилией студента - так же, как и в задании 2; таким образом, α0 = αАВ; αn - дирекционный угол стороны ПЗ 19 - П3 20; для всех вариантов берется на 10°32,8' больше исходного дирекционного угла α0. Пример. Если α0 = 29°34,2', то αn = 29°34.2'+10°32,8' 3. Отметки пунктов П38 и ПЗ 19 должны быть известны из геометрического нивелирования. При выполнении же задания значение отметки ПЗ 8 следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра студента. В дробной части отметки (дм, см, мм) ставятся те же цифры, что и в целой части. Пример:
Отметка ПЗ 19 для всех вариантов принимается на 3,282 м больше отметки ПЗ 8. 4. При съемке участка были составлены абрисы (рис. 3, а, б и 4, а - г). УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.006 с.) |




 ;
;  .
. и
и  - приращения координат, вычисляемые из соотношений:
- приращения координат, вычисляемые из соотношений: ;
;  .
.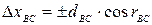 и
и 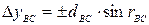 .
.

 = +225,31;
= +225,31;  = +80,15.
= +80,15. +
+
 +
+


 и
и  точки С будут использованы в следующем задании.
точки С будут использованы в следующем задании.




 принимается равным значению
принимается равным значению 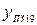 - значению
- значению 


