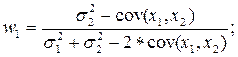Формирование оптимального инвестиционного портфеля на основе

Теории Г. Марковица

 

Из предыдущего параграфа видно, что большинство инвестиционных стратегий имеют цель оптимального сочетания риска и доходности при формировании инвестиционного портфеля. Теоретический базисом оптимизации соотношения «риск – доходность» по портфелю является разработанная в 50-е г.г. ХХ в. Г. Марковицем теория инвестиционного портфеля. Ниже кратко изложены ее основные положения.

Прежде всего, под риском в рамках данной теории понимается возможность изменения доходности по тому или иному активу. В свою очередь, изменение доходности измеряется степенью ее разброса: либо среднеквадратическим отклонением σ, либо дисперсией D.

Анализ «риск – доходность» проводится в осях (координатах): математическое ожидание доходности μ – среднеквадратическое отклонение доходности σ. Ниже отражена взаимосвязь μ, σ и вероятности сценария доходности р.

р_i = (x_i – μ) / σ; μ = Σ x_i / n; μ = Σ (x_i * р_i);

σ = √D = √Σ (x_i – μ)² / n; σ = √D = √Σ [(x_i – μ)² * р_i], (1)

где x_i – значение доходности; i – сценарий / момент времени;

n – число моментов времени.

Стоит пояснить, что формулы (1) предполагают возможность проведения двух вариантов анализа: с использованием вероятностей и без таковых. В первом случае анализируются возможные сценарии доходности, во втором – динамика за предшествующий период времени.

Одним из основополагающих принципов теории Г. Марковица является утверждение о том, что риск по совокупности (портфелю) из двух и более бумаг (активов) в большинстве случаев оказывается ниже, чем по каждой из них в отдельности. В подтверждение этого приведем числовой пример.

В примере предполагается вариант анализа с использованием вероятностей. Исходные данные и результаты расчета доходности представлены в табл.1, 2.

Таблица 1.

Исходные данные для анализа «риск – доходность»

Активы	Цена актива	Возвратный поток (прогноз)
Р=0,3	Р=0,4	Р=0,1	Р=0,2
Акция 1
Акция 2				169,5

Таблица 2.

Результаты расчета доходности активов*

Активы	Р=0,3	Р=0,4	Р=0,1	Р=0,2	μ
Акция 1	0,03	0,15	0,19	0,12	0,112
Акция 2	0,1	0,1	0,13		0,083

*Сценарий доходности рассчитывается следующим образом.

Для акции 1, при Р=0,3: доходность = (206 – 200) / 200 = 0,03.

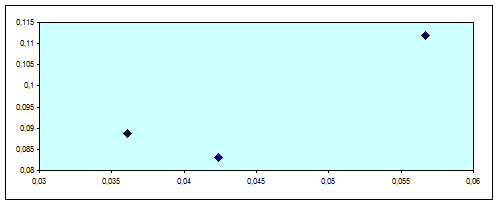
Рассчитаем среднеквадратическое отклонение σ по каждому активу.

s 1 = √0,3 (0,03 – 0,112) ² + 0,4 (0,15 – 0,112) ² + 0,1 (0,19 – 0,112) ² +

+ 0,2 (0,12 – 0,112) ² = 0,0567.

s 2 = √0,3 (0,1 – 0,083) ² + 0,4 (0,1 – 0,083) ² + 0,1 (0,13 – 0,083) ² +

+ 0,2 (0 – 0,083) ² = 0,0424.

Затем рассчитаем те же показатели для совокупности из двух акций при исходной структуре портфеля 20% бумаги 1 на 80% бумаги 2. Ниже представлен расчет доходности по четырем сценариям (по вероятности).

((206 – 200) / 200) * 0,2 + ((165 – 150) / 150) * 0,8 = 0,086.

((230 – 200) / 200) * 0,2 + ((165 – 150) / 150) * 0,8 = 0,11.

((238 – 200) / 200) * 0,2 + ((169,5 – 150) / 150) * 0,8 = 0,142.

((224 – 200) / 200) * 0,2 + 0 * 0,8 = 0,024.

Далее рассчитаем μ, σ по портфелю из двух бумаг.

μ _комб. = 0,3 * 0,086 + 0,4 * 0,11 + 0,1 * 0,142 + 0,2 * 0,024 = 0,0888.

s _комб. = √0,3 (0,086 – 0,0888) ² + 0,4 (0,11 – 0,0888) ² + 0,1 (0,142 – 0,0888) ² +

+ 0,2 (0,024 – 0,0888) ² = 0,0361.

Теперь сравним расчеты μ, σ для бумаг в отдельности и по их портфелю:

по σ: 0,0361 < 0,0424; 0,0361 < 0,0567.

по μ: 0,0888 < 0,112; 0,0888 > 0,083.

Таким образом, риск по портфелю меньше, чем по каждой бумаге в отдельности, при доходности большей, чем по второй бумаге и меньшей, чем по первой бумаге. Для большей наглядности, изобразим результаты расчетов графически, как показано на рис.1.

Основной целью портфельной теории Г. Марковица является выявление оптимальной комбинации долей активов в портфеле, для достижения наилучшего сочетания риска и доходности. Первый шаг на этом пути – построение области значений «риск – доходность» при долях w активов в портфеле от «0» до «1».

Для портфеля из двух активов, как для самого простого случая, эта область может быть изображена графически, как показано на рис.2.

 

Рис. 1. Результаты расчета риска и доходности по портфелю активов

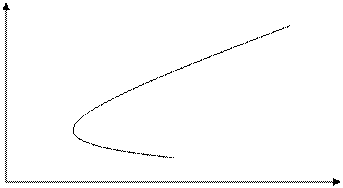
μ

 

 

s

Рис. 2. Область значений «риск – доходность» для портфеля из двух активов

Фактически, кривая на рис.2 – это не что иное, как точки на рис.1, соединенные плавными линиями, по мере возрастания доли w по одному активу и одновременного убывания по другому.

В теории Г. Марковица установлены рекуррентные соотношения, связывающие минимальный риск в целом по портфелю с рисками по каждому из активов, и определяющие структуру портфеля. Эти соотношения даны ниже.

s _комб. = √ w₁² * s₁² + 2 * w₁ * w₂ * cov (x₁, x₂) + w₂² * s₂² , откуда

сov (x₁, x₂) = Σ [(x₁ – μ) * (x₂ – μ) * p]

cov (x₁, x₂) = сorr (x₁, x₂) * s₁ * s₂ (2)

где сov (x₁, x₂) – ковариация колебаний доходности активов в портфеле;

сorr (x₁, x₂) – корреляция доходности активов в портфеле.

Уточним, что риск по портфелю, определяемый по формуле (2), соответствует точке экстремума на кривой, отображающей область значений «риск – доходность» на рис.2. Как видно из рис.2, минимум риска не совпадает с максимумом возможного дохода, т.е. эти два условия не могут быть достигнуты одновременно. Отсюда следует, что структура портфеля, определяемая по формуле (2), не является строго оптимальной.

Определение строго оптимальной структуры портфеля, согласно теории Г.Марковица, связано с введением дополнительного инструментария – кривых безразличия, или изопредпочтений инвестора. По аналогии с кривыми безразличия, применяемыми в макроэкономике для определения наилучшего для потребителя сочетания 2-х продуктов, кривые изопредпочтений отображают комбинации 2-х активов в портфеле с равнозначным для инвестора сочетанием риска и доходности.

Построение кривых безразличия основано на варьировании предпочтений инвестора с помощью коэффициента α. Для расположенных к риску инвесторов вводится α >0, для не склонных к риску – α <0. Кривая безразличия задается с помощью функции предпочтений инвестора, имеющей следующий вид.

F = μ + α * s ²; F = μ + α² * s ²; F = μ + α * s ⁿ; F = μ + αⁿ * s ⁿ. (3)

Тогда строго оптимальная структура портфеля определяется как точка пересечения кривых области значений «риск – доходность» и изопредпочтений инвестора. Графически это показано на рис.3.

Проблема нахождения оптимальной точки, показанной на рис.3, осложняется необходимостью подбора как функции предпочтения из формул (3), так и соответствующего нулевому риску математического ожидания доходности, являющегося отправной точкой для кривой безразличия.

 

μ

 

 

s

Рис.3. Определение строго оптимальной структуры инвестиционного портфеля

Портфельная теория Г.Марковица имеет два важных практических приложения: модель оценки финансовых активов САРМ (capital asset pricing model) и критерии оценки качества управления ими.

Модель оценки финансовых активов (САРМ), как и любая другая модель, является упрощением реальной действительности, и, поэтому, содержит в себе упрощающие предпосылки. Они касаются поведения инвесторов на фондовом рынке и их перечень следующий:

- все инвесторы руководствуются принципом «m – s»;

- все инвесторы имеют одинаковый объем информации о возможных альтернативах вложения средств и связанных с ними потоках доходов;

- все участники рынка меняют количества, а не виды ценных бумаг;

- всегда есть возможность инвестирования по безрисковой ставке процента.

Любой инвестор стремится достичь оптимального сочетания риска и доходности по портфелю из активов, состав которого (но не структура долей) остается неизменным. Как уже было показано ранее, оптимальное сочетание риска и доходности по портфелю достигается в точке пересечения кривых их возможных значений и изопредпочтений инвестора. В модели САРМ кривая изопредпочтений заменяется на линию рынка капитала.

После отсечения случайных рисков в модели САРМ путем допущения идеального поведения инвесторов на фондовом рынке остаются только риски, присущие рынку в целом. Модель САРМ отражает систематический риск инвестирования в финансовые активы как связь изменения средней доходности на рынке ценных бумаг определенного типа с изменением доходности отдельной ценной бумаги. Эта связь выражается с помощью коэффициента β, который рассчитывается, как показано ниже.

β = cov (д _и, д _р) / D (д _р), (6)

где cov (д _и, д _р) – ковариация доходности по отдельной (индивидуальной) бумаге и по рынку данного класса активов в целом;

D (д _р) – дисперсия доходности на рынке данного класса активов в целом.

Сама модель САРМ имеет вид, отраженный в формуле (7).

k _р. = k _б.р. + β * (k _а. – k _б.р.), (7)

где k _б.р. – безрисковая ставка дохода; k _а – фактическая доходность по активу;

k _р. – требуемая с учетом систематического риска ставка дохода по активу.

Вторым практическим приложением портфельной теории Г. Марковица являются критерии оценки качества управления активами. К ним относят критерии Тренора, Шарпа и ряд других. Эти критерии применяют в своей деятельности управляющие компании ПИФов. Суть этих критериев сводится к сравнению двух одинаковым способом рассчитываемых величин по портфелю, управляемому тем или иным менеджером, и по совокупности активов, находящихся в управлении ПИФа в целом.

Методика определения критериев Тренора TRN и Шарпа SHP и оценки качества управления активами на их основе отражена в формулах ниже.

TRN _i = (R _i – RFR) / β _i; TRN _ПИФ = (R _ПИФ – RFR) / β; TRN _i > TRN _ПИФ.

SHP _i = (R _i – RFR) / σ _i; SHP _ПИФ = (R _ПИФ – RFR) / σ _ПИФ; SHP _i > SHP _ПИФ. (8)

где R _i – доход по i-му портфелю; RFR – безрисковая ставка дохода.

Как видно из формул (8), критерии Тренора и Шарпа различаются лишь способом измерения риска: у первого – это β, определяемая по формуле (6), а у второго – это σ, определяемая по формулам (1). По отношению к i-му портфелю определяется взаимосвязь (β) изменения его доходности с изменением доходности по ПИФу в целом. Для ПИФа – взаимосвязь изменения доходности по ПИФу с изменением доходности на фондовом рынке в целом. Знак «>» в правой части формул (8) отражает хорошее качество управления портфелем, «<» – плохое.

Раздел 2. Особенности финансирования инвестиционных проектов

банковскими учреждениями и на фондовых рынках стран Евросоюза