
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шкала оцінювання в кмсонп та еctsСодержание книги
Поиск на нашем сайте
П.Ф.Турчин ФІЗИЧНА ТА КОЛОЇДНА ХІМІЯ Інтерактивний комплекс навчально-методичного забезпечення
Кредитно-модульна система організації навчального процесу
Для студентів за напрямом підготовки „Екологія”
Рівне – 2008
УДК 54.18 ББК 24.6 Т 89 Затверджено вченою радою Національного університету водного господарства та природокористування (Протокол № 12 від 29 листопада 2008 р.)
Рецензенти: Клименко М.О., доктор сільськогосподарських наук, професор Національного університету водного господарства та природокористування; Яцков М.В., кандидат технічних наук, професор Національного університету водного господарства та природокористування.
Турчин П.Ф. Т 89 Фізична та колоїдна хімія: Інтерактивний комплекс навчально-методичного забезпечення. – Рівне: НУВГП, 2008. – 269 с.
Інтерактивний комплекс навчально-методичного забезпечення дисципліни „Фізична та колоїдна хімія” написаний відповідно до програми дисципліни. Він складається з 6 розділів, в яких подано типову програму, повний обсяг теоретичного матеріалу, тематика лабораторних робіт, методичні вказівки до виконання розрахункової роботи, запитання для самоконтролю, завдання для самоконтролю, завдання для самостійної і розрахункової роботи. Навчально-методичний посібник розроблено на основі сучасної хімічної літератури, ілюстровано схемами, таблицями, рисунками, діаграмами, рівняннями реакцій. Посібник призначено для студентів напряму „Екологія, охорона навколишнього середовища та збалансоване природокористування”. Він буде корисним студентам, аспірантам, науковим працівникам, фахівцям біологічного профілю. Табл.16, рис.130 бібліограф.: 22 УДК 543 ББК 24.6 © Турчин П.Ф., 2008 © НУВГП, 2008
ПЕРЕДМОВА
Концепції розвитку і реформування вищої освіти України в контексті Болонського процесу передбачають впровадження кредитно-модульної системи організації навчального процесу. Впровадження кредитно-модульного навчання вимагає урізноманітнення форм і змісту індивідуальної роботи студента, що може бути здійснено відповідним науково-методичним забезпеченням навчальних дисциплін. Головною метою навчальної дисципліни „Фізична та колоїдна хімія” студентами напряму підготовки 6.040106 „Екологія, охорона навколишнього середовища та збалансоване природокристуван-
ня” є: - вивчення студентами теоретичних основ фізичної та колоїдної хімії, опанування науково-обгрунтованими підходами до оцінки і використання поверхневих явищ, колоїдно-хімічних процесів, дисперсних систем, які зустрічаються в різноманітних технологічних процесах. Студенти повинні знати: фізичні і хімічні процеси і явища технологічних виробництв, виконувати термодинамічні розрахунки, пов’язані з технологічними процесами, кількісно оцінювати їх оптимальні параметри. Студенти повинні вміти: оволодіти навичками експериментальної роботи в фізико-хімічній лабораторії, вміти користуватись основними приладами, лабораторною технікою та хімічним посудом, фіксувати та пояснювати спостереження і результати експериментальних досліджень, виконувати розрахунки на їх основі, навчитись узагальнювати результати дослідів у вигляді висновків і заключень.
ТИПОВА ПРОГРАМА НОРМАТИВНОЇ НАВЧАЛЬНОЇ ДИСЦИПЛІНИ „ФІЗИЧНА ТА КОЛОЇДНА ХІМІЯ” 1. ОПИС ПРЕДМЕТА НАВЧАЛЬНОЇ ДИСЦИПЛІНИ „ФІЗИЧНА ТА КОЛОЇДНА ХІМІЯ” Таблиця 1
Характеристика предмета навчальної дисципліни „Фізична та колоїдна хімія”
продовження табл. 1
ІІ. РОЗПОДІЛ БАЛІВ, ЩО ПРИСВОЮЮТЬСЯ СТУДЕНТАМ
Таблиця 2 2.1. Таблиця розподілу балів, що присвоюються студентам
Шкала оцінювання в КМСОНП та ЕCTS
ІІІ. ПРОГРАМА НАВЧАЛЬНОЇ ДИСЦИПЛІНИ
Таблиця 3 Тематичний план та розподіл навчального часу
продовження табл. 3
IV. ПРОГРАМНИЙ МАТЕРІАЛ БЛОКІВ ЗМІСТОВИХ МОДУЛІВ Блок 1. „Фізична хімія” Тема 1. Основи хімічної термодинаміки та практичне застосування її положень в хіміко-технологічних розрахунках Загальні відомості. Ентальпія. Теплоємність. Перший закон термодинаміки. Теплові ефекти хімічних реакцій. Закон Гесса. Залежність теплових ефектів хімічних реакцій від температури. Другий закон термодинаміки. Ентропія. Енергія Гіббса. Напрямок хімічної реакції. Теплота фазових перетворень. Практичне застосування термодинамічних розрахунків.
Тема 2. Розчини. Термодинаміка розчинів Основні поняття. Розчинність речовин у воді. Кінетика розчинення твердих речовин. Теплота розчинення. Змішування і розчинення рідин. Насичені і пересичені розчини. Залежність розчинності електролітів від йонної сили розчину. Йонно-молекулярні рівноваги в розчинах електролітів.
Тема 3. Хімічна кінетика Класифікація хімічних реакцій. Швидкість хімічних реакцій. Молекулярність і порядок хімічних реакцій. Складні реакції. Кінетика ферментативних реакцій. Тема 4. Фазові рівноваги Основі поняття й означення. Однокомпонентні системи. Рівноваги рідин з газовою фазою. Рухомі рівноваги у атмосферному повітрі. Діаграми рівноваг рідина-пара в бінарних системах. Двокомпонентні системи. Трикомпонентні системи.
Блок 2. „Колоїдна хімія”
Тема 5. Фізико-хімія поверхневих явищ. Адсорбція Поверхневі явища і їх значення. Дисперсність. Питома поверхня і вільна поверхнева енергія. Когезія та адгезія. Змочування та розтікання. Капілярність. Адсорбція. Адсорбція на межі поділу рідина-газ. Адсорбція на межі поділу тверде тіло-газ. Адсорбція на межі поділу конденсованих фаз. Полімолекулярна адсорбція. Теорія БЕТ. Поверхневі явища на межі поділу тверде тіло-рідина. ЗМІСТОВИЙ МОДУЛЬ 1 ФІЗИЧНА ХІМІЯ Тема 3. Хімічна кінетика
Класифікація хімічних реакцій. Усі хімічні реакції проходять або в гомогенних системах, що складаються лише з однієї фази, або в гетерогенних, які складаються з двох і більше фаз. Такі реакції називаються відповідно гомогенними і гетерогенними. В гетерогенних системах одна із фаз завжди перебуває в диспергованому стані, тому хімічна взаємодія в них відбувається на поверхні поділу фаз. Розрізняють двофазні системи „рідина-тверда фаза”, „рідина-рідина” (що взаємонерозчинні), „газ-рідина”, “газ-тверда речовина”, „тверда речовина – тверда речовина”. Гетерогенні реакції відбуваються досить повільно ніж гомогенні. Це обумовлено складністю їх механізму: дифузія до поверхні поділу фаз, хімічна взаємодія реагентів, дифузія продуктів реакції від поверхні поділу фаз, поверхневі явища та ін. За механізмом усі реакції можна поділити на дві групи: прості і складні. Прості реакції складаються із однієї стадії – хімічного перетворення. За ознакою молекулярності вони поділяються на одномолекулярні (мономолекулярні), двомолекулярні (бімолекулярні), тримолекулярні. До складних реакцій відносяться ланцюгові, спряжені, паралельні, послідовні, оборотні, фотохімічні радіаційно-хімічні, ферментативні, гомогенно-гетерогенні. Для складних реакцій молекулярність можна визначити тільки для їх окремих стадій. Усі хімічні реакції формально поділяють на реакції першого, другого і третього порядків, а також нульового і дробного порядків. Під порядком реакції розуміють суму показників ступенів при змінюючих концентраціях реагентів в кінетичному рівнянні. Суму стехіометричних коефіцієнтів вихідних речовин, що одночасно беруть участь в елементарному акті реакції, прийнято визначати як її молекулярність. На швидкість гомогенних гетерогенних реакцій впливають: природа реагуючих речовин, концентрація речовин, тиск, температура, наявність каталізатора (ферментів). У випадку гетерогенних реакцій на їх швидкість також впливає ступінь диспергованості (поверхня поділу фаз) речовин.
Знаючи хімічну кінетику реакцій можна визначати оптимальні параметри і умови проведення різних хіміко-технологічних і біохімічних процесів, які відбуваються при виробництві хімічних матеріалів, синтезу біологічних речовин, нейтралізації і знешкодження шкідливих речовин, забруднювачів навколишнього середовища. Швидкість хімічної реакції. Кінетичні закономірності перебігу хімічних реакцій ґрунтуються на припущенні про те, що реагують тільки ті молекули, які стикаються між собою. Кількість таких зіткнень прямо пропорційна кількості молекул, тому швидкість реакції повинна бути пропорційною концентрації реагуючих речовин (закон діючих мас). Для емпіричного рівняння:
Швидкість прямої реакції можна записати як:
де v - швидкість хімічної реакції; З рівняння випливає, що швидкість реакції, будучи функцією концентрації, залежить також від часу, оскільки концентрація реагуючих речовин з часом змінюється.
На рисунку 3.1 приведені графічні залежності зміни концентрації вихідного реагенту (крива 1) і продукту реакції (крива 2) з часом, а також середня і істина швидкості хімічної реакції.
Для заданого інтервалу часу
де За умови, що
швидкість хімічної реакції в даний момент часу відповідає значенню миттєвої (істинної) швидкості реакції v:
Для реагенту А середня швидкість реакції виразиться як:
В той же час, для продукту реакції D швидкість реакції буде мати знак плюс:
тому, що його концентрація збільшується. Швидкість реакції в даний момент часу можна визначити графічним способом. Для цього до точки на кривій зміни концентрації реагенту А, яка відповідає даному моменту часу (приклад Отже, хімічна кінетика визначає поняття швидкості гомогенної реакції як зміну концентрації одного з реагуючих компонентів за одиницю часу в одиниці об’єму (при постійній температурі):
де Гетерогенні реакції відбуваються на поверхні
У рівнянні швидкості прямої реакції коефіцієнт пропорційності
За цих умов:
Це і є фізичний зміст коефіцієнта На константу швидкості впливає в основному температура. Фактор впливу температури на константу швидкості гомогенної реакції виражає рівняння Арреніуса:
де А і В – характерні для даної реакції сталі, що не залежать від температури.
Рівняння Арреніуса в диференціальній формі має вигляд:
Величина Е називається арреніусовською енергією активації. Її розглядають як енергетичний бар’єр, що подолають лише активні молекули. Значення енергії активації дістають з експериментальних даних. Для цього будують графічну залежність lnk і 1/T в прямокутній системі координат. Ця залежність є прямою лінією, за кутом нахилу якої визначають енергію активації реакції:
де m - відношення масштабу по осі абсцис до масштабу по осі ординат. Відрізок, що відсікається продовженням прямої на осі ординат, відповідає ln/k0. Знаючи константу швидкості при двох значеннях температури, можна розрахувати енергію активації:
Енергію активації можна визначити і за виразом:
Вплив температури і енергії активації на швидкість хімічних реакцій можна виразити рівнянням Арреніуса в експоненціальному вигляді:
де Якщо концентрації реагуючих речовин дорівнюють 1 моль/л, то рівняння Арреніуса дає змогу виразити залежність швидкості реакції від температури:
Оскільки в рівнянні температура входить у показник ступеня, то швидкість хімічних реакцій значною мірою залежить від зміни температури. Згідно з емпіричним правилом Вант-Гоффа: підвищення температури на кожні 10 градусів збільшує швидкість реакції приблизно в 2 - 4 рази. У математичній формі правило Вант-Гоффа записується так:
де Температурний коефіцієнт можна знайти за виразом:
Рівняння Вант-Гоффа є приблизним, оскільки швидкість реакції, крім температури залежить також від енергії активації, яка в свою чергу, залежить від температури. Молекулярність і порядок хімічних реакцій. Молекулярніть простої реакції можна пов’язати із стехіометричним рівнянням. Наприклад, реакція розкладання пероксиду гідрогену:
є мономолекулярною, а реакція синтезу хлориду гідрогену:
бімолекулярною. Прикладом тримолекулярної реакції є реакція синтезу води з Гідрогену і Оксигену:
Найчастіше реакції бувають бімолекулярними, тримолекулярні реакції трапляються рідко, а більш молекулярні взагалі невідомі. Для елементарних реакцій порядок, як правило, співпадає з їхньою молекулярністю. Складні реакції здійснюються через проміжні стадії, які забезпечують найбільшу швидкість реакції. Для таких реакцій порядок не співпадає з коефіцієнтами сумарного стехіометричного рівняння. Наприклад, мономолекулярна реакція розкладання пероксиду гідрогену може відбуватися, як бімолекулярна:
Порядок цієї реакції повинен бути другим. Проте насправді, залежно від умов, порядок цієї реакції є першим або дробовим. У тих випадках, коли за умовами експерименту різниця між концентраціями вихідних речовин дуже велика порядок реакції також не співпадає з її молекулярністю. Порядок реакції на практиці визначають методом ізоляції Оствальда. Згідно цього метода усі реагенти, крім одного, беруть з надлишком (їх концентрація практично стала в ході реакції) і тому їх вводять в константу швидкості. Тоді, для реагента А концентрація, якого змінюється, вираз швидкості реакції буде мати вигляд:
Рівняння логарифмують:
і будують графічну залежність
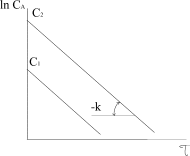
Реакції нульового порядку. Гомогенних хімічних реакцій нульового порядку, в принципі, не існує. Але, якщо речовина, за якою контролюється хід реакції, не бере участі в лімітуючій стадії складного процесу швидкість реакції не залежить від концентрації реагенту і графічно виражається прямою лінією (див.рисунок). Тип таких реакцій називається реакціями нульового порядку:
де
Нульовий порядок спостерігається в гетерогенних реакціях в яких швидкість витрачання речовини значно менша від її надходження. До реакції нульового порядку також належать процеси ферментативного каталізу. Поєднуючи рівняння
Інтегрування цього рівняння призводить до рівняння:
Яке дає змогу визначити константу швидкості реакцій нульового порядку. Кінетичне рівняння хімічної реакції нульового порядку має вигляд:
Експериментально константу швидкості можна знайти, користуючись графічною залежністю За кінетичним рівнянням хімічної реакції нульового порядку константа швидкості реакції залежить від способу вираження концентрації вихідної речовини:
Користуючись значеннями величини константи швидкості, можна розрахувати час закінчення реакції
Для визначення періоду напівперетворення – час, за який концентрація вихідних речовин зменшується в два рази, застосовуємо рівняння:
Кількість речовини х, що прореагувала за час
і ввести у кінетичне рівняння реакції:
де а – початкова концентрація реагенту при При
Реакції першого порядку. До них належать реакції ізомеризації, термічного розкладання речовин, радіоактивного розпаду атомних ядер, багато бімолекулярних реакцій при умові, що концентрація одної із речовин, що реагує, підтримується постійною. Для необоротної реакції першого порядку типу:
швидкість реакції у диференціальній формі запишемо так:
в інтегральній формі:
в експоненціальній формі:
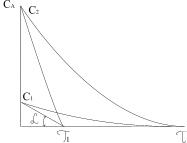
де На рисунку 3.6 приведена залежність
звідки:
Рівняння в інтегральній формі дає можливість визначити константу швидкості необоротної реакції першого порядку:
Величина k не залежить від способу вираження концентрації, її розмірність становить с-1 або хв.-1. За рівнянням 3.25 залежність Згідно з цим рівнянням розв’язання двох рівнянь з різними значеннями
Що дозволяє визначити k без знаходження початкової концентрації речовини. Для оцінки k можна скористатися любою іншою величиною, якщо вона пропорційна концентрації, наприклад, електропровідністю, оптичною густиною та ін. Період напівперетворення для необоротної реакції першого порядку не залежить від початкової концентрації реагуючих речовин і дорівнює:
Кількість речовини х, що прореагувала за час
де а – концентрація на початку реакції. Якщо замість концентрації скористатися ступенем перетворення
Кінетика обротних реакцій ускладнюється одночасним протіканням оборотної реакції. Прикладом оборотних реакцій є синтез амоніаку, окиснення оксиду сульфуру(IV), реакції рацемізації і ізомеризації, в тому числі оптичної ізомеризації, наприклад ізомеризації Для оборотної реакції, що відбувається при сталому об’ємі за стехіометричним рівнянням:
справджується така залежність:
При досягненні рівноважного стану константа хімічної рівноваги
де Враховуючи, що
рівняння (3.30) після перетворень матиме вигляд:
в інтегральній формі:
Початкова швидкість оборотної реакції становитиме:
З цього рівняння випливає, що
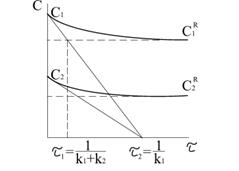
На рисунку 3.8 залежності
Дотичні для
Час
оскільки на початку процесу добуток У випадку, коли
тоді
Реакції другого порядку. Реакцією другого порядку називають реакцію, швидкість якої пропорційна або добутку концентрацій двох реагуючих речовин ( До них належать реакції розкладання, обміну і сполучення:
Так, реакція розкладання пероксиду гідрогену, яка вже згадувалась, при більш високих температурах відбувається не по першому порядку, а по другому:
Для такого типу необоротних реакцій другого порядку рівняння швидкості (при
Коефіцієнт 2 в рівнянні вказує на те, що в кожному елементарному акті хімічної взаємодії беруть участь дві молекули речовини А. Здійснюючи поділ змінних і, інтегруючи від
звідки:
Розмірність Відповідно з рівняння 3.36:
лінійна залежність в координатах Період напівперетворення речовини А обернено пропорційний початковій концентрації реагуючих речовин:
На рисунку 3.9 періоди напівперетворень зображені точками перетину прямої залежності з абсцисою. Щоб визначити кількість речовини х, яка прореагувала за проміжок часу
з рівняння 3.37 одержимо:
де -
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.170.19 (0.016 с.) |


 (3.1)
(3.1)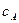 і
і 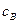 - концентрації реагуючих речовин; а і b - їх стехіометричні коефіцієнти. Правило, виражене рівнянням, називають основним постулатом хімічної кінетики.
- концентрації реагуючих речовин; а і b - їх стехіометричні коефіцієнти. Правило, виражене рівнянням, називають основним постулатом хімічної кінетики.
 реагентів А (1) і
D (2) з часом
реагентів А (1) і
D (2) з часом  для реакції aA+bB=cC+dD
для реакції aA+bB=cC+dD
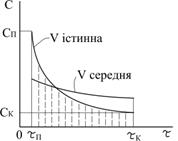
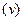
 можна ввести поняття про середню швидкість реакції
можна ввести поняття про середню швидкість реакції  (рис.3.2):
(рис.3.2): (3.2)
(3.2) і
і  - концентрація реагенту А в початковій
- концентрація реагенту А в початковій  і кінцевий
і кінцевий 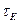 момент часу.
момент часу.
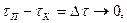
 (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5)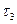 ) проводять дотичну. Тангенс кута нахилу
) проводять дотичну. Тангенс кута нахилу  дотичної до кривої відповідає швидкості реакції.
дотичної до кривої відповідає швидкості реакції.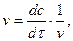 (3.6)
(3.6) - об’єм реакційного елемента.
- об’єм реакційного елемента. поділу фаз (каталізатора), яка в момент взаємодії реагентів практично не змінюється. Тому швидкість гетерогенних реакцій описується рівнянням:
поділу фаз (каталізатора), яка в момент взаємодії реагентів практично не змінюється. Тому швидкість гетерогенних реакцій описується рівнянням: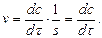
 не залежить від концентрації реагуючих речовин. Його фізичний зміст можна знайти, якщо прийняти, що концентрації реагуючих речовин А і В дорівнюють одиниці, тобто
не залежить від концентрації реагуючих речовин. Його фізичний зміст можна знайти, якщо прийняти, що концентрації реагуючих речовин А і В дорівнюють одиниці, тобто
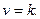
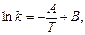 (3.7)
(3.7)
 (3.8)
(3.8)
 (3.9)
(3.9)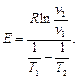 (3.10)
(3.10) (3.11)
(3.11) - передекспоненціальний множник, пропорційний числу зіткнень молекул.
- передекспоненціальний множник, пропорційний числу зіткнень молекул. (3.12)
(3.12) (3.13)
(3.13)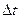 - збільшення температури;
- збільшення температури;  і
і  - швидкість реакції до
- швидкість реакції до  і після підвищення температури до
і після підвищення температури до  ;
; 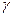 - температурний коефіцієнт швидкості реакції
- температурний коефіцієнт швидкості реакції 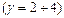 .
. (3.14)
(3.14)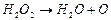
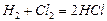
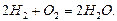
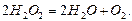
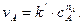 (3.15)
(3.15)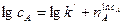 (3.16)
(3.16)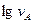 від
від 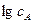 . Тангенс кута нахилу прямої цієї залежності відповідає
. Тангенс кута нахилу прямої цієї залежності відповідає 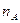 . Аналогічно визначають порядки реакції за всіма іншими реагентами.
. Аналогічно визначають порядки реакції за всіма іншими реагентами.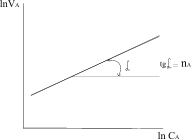
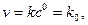 (3.17)
(3.17)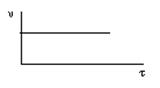
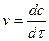 і
і 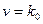 маємо:
маємо: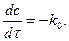 (3.18)
(3.18)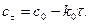 (3.19)
(3.19)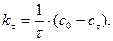 (3.20)
(3.20)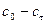 від
від 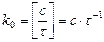 моль/(л. с).
моль/(л. с).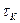 :
: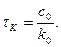

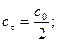
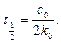
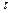 , можна розрахувати, якщо прийняти:
, можна розрахувати, якщо прийняти: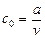
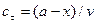

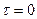 ; х – кількість речовини, що прореагувала за час
; х – кількість речовини, що прореагувала за час 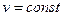 :
: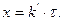
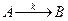
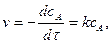 (3.22)
(3.22)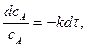 (3.23)
(3.23) (3.24)
(3.24)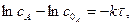 (3.25)
(3.25) (3.26)
(3.26)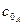 - початкова концентрація речовини А.
- початкова концентрація речовини А. для двох різних значень початкової концентрації
для двох різних значень початкової концентрації 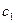 і
і 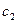 . Дотичні до кривих залежності, як бачимо, перетинаються на абсцисі в одній точці
. Дотичні до кривих залежності, як бачимо, перетинаються на абсцисі в одній точці 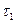 , величина якої не залежить від початкової концентрації речовини А. Час
, величина якої не залежить від початкової концентрації речовини А. Час 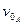 :
: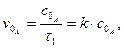
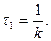
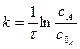
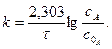 (3.27)
(3.27)
 від
від 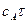 дає:
дає: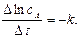
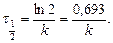 (3.28)
(3.28)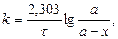 (3.29)
(3.29)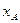 , то кінетичне рівняння матиме вигляд:
, то кінетичне рівняння матиме вигляд: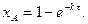
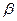 -глюкозу.
-глюкозу.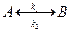
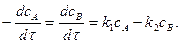 (3.30)
(3.30)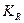 буде дорівнювати:
буде дорівнювати: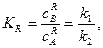
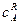 і
і 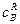 - концентрація речовин в стані рівноваги.
- концентрація речовин в стані рівноваги.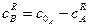
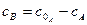
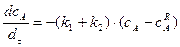 (3.31)
(3.31)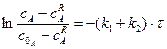
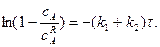
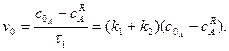 (3.33)
(3.33)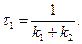
 для
для 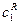 .
.
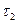 , величина якої не залежить від початкової концентрації речовини А. В цьому випадку швидкість реакції становитиме:
, величина якої не залежить від початкової концентрації речовини А. В цьому випадку швидкість реакції становитиме: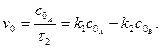 (3.34)
(3.34)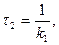
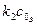 дорівнює нулю.
дорівнює нулю.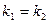 маємо:
маємо: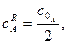
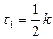
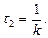
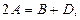
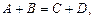
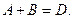
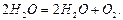
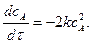 (3.35)
(3.35)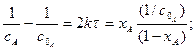 (3.36)
(3.36)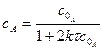
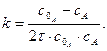 (3.37)
(3.37)
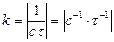 , тобто числове значення k залежить від способу вираження концентрації:
, тобто числове значення k залежить від способу вираження концентрації: 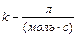 .
.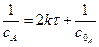
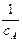 від
від 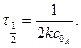 (3.38)
(3.38)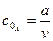 і
і 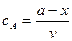
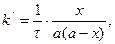 (3.39)
(3.39)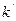 - замість 2k; а – маса реагуючої речовини в початковій момент.
- замість 2k; а – маса реагуючої речовини в початковій момент.
 від
від 


