
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Основи хімічної термодинаміки та практичне застосування її положень в хіміко-технологічних розрахункахСодержание книги
Поиск на нашем сайте
Термодинаміка вивчає макросистеми в яких, без проведення експериментів, існує принципова можливість визначення проходження того чи іншого процесу і його напрямку. Розрізняють різні напрямки термодинаміки. В нашому випадку ми розглядаємо хімічну термодинаміку, яка вивчає застосування її основних законів стосовно до фізико-хімічних і хімічних явищ. До цих явищ відносяться хімічні реакції і фазові перетворення (розчинення, випаровування, кристалізація чистих речовин і розчинів і зворотні їм процеси), адсорбція і ін. Найважливішими напрямками розвитку хімічної термодинаміки є вчення про хімічні і фазові рівноваги, вчення про розчини (особливо про розчини електролітів), термодинаміка поверхневих явищ і ін. В основі хімічної термодинаміки лежать загальні положення і висновки (закони) термодинаміки. Вивчення законів термодинаміки дає змогу використовуючи термодинамічний аналіз визначати напрям процесу і оптимальні умови ведення технологічного режиму, встановлювати межі раціонального вилучення цільових продуктів, забезпечувати вихід шкідливих речовин і забруднення навколишнього середовища, тощо. Термодинамічною системою називається сукупність тіл, що енергетично взаємодіють між собою і іншими тілами, а також обмінюються між ними речовиною. Взаємодія системи із навколишнім середовищем супроводжується передачею теплоти і виконанням роботи. Робота витрачається на переборення зовнішніх сил, які порушують рівновагу системи, або відбувається обмін енергією. Повна енергія термодинамічної системи поділяється на зовнішню і внутрішню. Внутрішня енергія системи складається з енергії всіх видів руху і взаємодії частинок (енергії поступального і обертового руху молекул, коливального руху атомів, енергії міжмолекулярної взаємодії, внутрішньоатомної і внутрішньоядерної енергії тощо). Зовнішня енергія включає енергію руху в цілому і потенціальну енергію системи. Для систем, які вивчаються, повна енергія дорівнює внутрішній енергії. Абсолютну енергію внутрішньої системи визначити неможливо, тому для термодинамічного аналізу достатньо знати зміну внутрішньої енергії системи DU. Коли система під дією сил виконує роботу це відповідає від¢ємному значенню DU, а коли процеси відбуваються без обміну енергії зі зовнішнім середовищем - додатному значенню DU. Зміна внутрішньої енергії, віднесена до одного моля, є функцією системи, її вимірюють у Дж/моль. Робота процесу А являє собою кількість енергії, що передається від одного тіла до іншого. Для елементарного процесу при сталому тиску (ізобарний процес), вираз для кількості роботи має вигляд P · D V. Її вимірюють у Дж. У термодинаміці вважають роботу, яку виконує система над зовнішнім середовищем (розширення газу, пароутворення, дисоціація, тощо) додатною (+A), а роботу, що виконується над системою (наприклад, стискання газу) - від¢ємною (-А). Якщо між системою і зовнішнім середовищем, відбувається порушення теплової рівноваги система поглинає або виділяє теплоту Q. Теплоту, яку система поглинає, вважають додатною (+Q), а теплоту, що виділяє система - від¢ємною (-Q). Теплоту як і роботу вимірюють в Дж. В той же час в термодинаміці тепловий ефект екзотермічної хімічної реакції є від¢ємним, а ендотермічної - додатнім. Якщо термодинамічна система не дістає і не віддає теплоту, то такий процес називається адіабатичним. Ентальпія. У термодинаміці поряд з внутрішньою енергією використовують функцію стану ентальпію H. Ентальпія - це енергія системи при сталому тиску. Вона чисельно дорівнює сумі внутрішньої енергії і потенціальної енергії (P · V):
Зміна ентальпії як і зміна внутрішньої енергії не залежать від шляху процесу, а залежать тільки від початкового та кінцевого стану. Тому в термодинаміці оперують зміною ентальпії DH як і DU відносять до одного моля речовини і вимірюють у Дж/моль. Тепловий ефект хімічної реакції, що відбувається при сталому тиску QP, дорівнює зменшенню ентальпії - DH:
Зміна ентальпії для речовин залежить від температури (рис.1.1).
Теплоємність - це кількість теплоти, яка потрібна для підвищення температури певної кількості речовини на один градус за відсутності фазового переходу і зміни її складу.
(істинна теплоємність при заданій температурі). Середню теплоємність
Розрізняють ізобарну теплоємність CP:
і ізохорну теплоємність CV:
Оскільки при ізохорному процесі вся теплота витрачається тільки на збільшення внутрішньої енергії системи, а при ізобарному ще й на роботу розширення, тому CP завжди більше CV. Отже для 1 моля ідеального газу зв'язок між CP і CV виражається залежністю:
де R - універсальна газова стала. За рівнянням Менделєєва-Клапейрона за нормальних умов
У розрахунках застосовують питому (розраховану на 1 г речовини) і молярну (на 1 моль) теплоємності, які мають відповідно розмірності: Дж/(г · к) і Дж/ (моль · К). Приблизну теплоємність речовин можна обчислити за правилом Дюлонга і Пті: добуток атомної маси елемента МА на його питому теплоємність С є сталою величиною. МА · С = n · (25,9 – 26,8) Дж/(моль · К). Наприклад, для сполуки Аl2O3, що складається з 5 атомів, теплоємність дорівнює: С = ((25,9 + 26,8): 2) · 5 = 132 Дж/(моль · К). Виняток з цього правила становлять Бор, Карбон і Силіцій. На величину теплоємності значною мірою впливає температура (рис.1.2).
При низьких температурах (до кімнатної) ця залежність описується рівнянням Дебая: , (1.7) де a - коефіцієнт, що залежить від природи речовини. Від кімнатної температури до температури плавлення теплоємність виражають у вигляді степеневих рядів:
де а, в, с..., а’, в’, с’.... – коефіцієнти, які визначають за експериментальними даними або за довідниками. Перший закон термодинаміки. Згідно з Гельмгольцем, перший закон термодинаміки встановлює зв’язок між кількістю теплоти, що підводиться із зовнішнього середовища до системи Q, роботою, яку виконує система A, та зміною внутрішньої енергії DU:
Рівняння є математичним виразом першого закону термодинаміки, яке свідчить що підведена із зовнішнього середовища теплота витрачається на виконання роботи і на збільшення внутрішньої енергії системи. Під час ізохорного процесу, коли об'єм системи сталий, тобто DV = 0, робота розширення, яку виконує система, дорівнює нулю, тоді рівняння набуває вигляду:
В цьому випадку вся теплота, яка надана системі, витрачається тільки на зміну її внутрішньої енергії. При ізотермічному процесі (T = const) внутрішня енергія не змінюється і DU = 0. Тоді рівняння буде мати вигляд:
або
тобто вся теплота, яка поглинається системою, перетворюється в роботу розширення. Для ізотермічного розширення 1 моля ідеального газу відповідатиме вираз:
а при адіабатичному процесі
або
Отже, зменшення внутрішньої енергії системи може виконувати роботу, а при стискуванні системи підвищується її температура і збільшується внутрішня енергія системи. Оскільки при ізобарному процесі P = const
або
де Dn - зміна числа молей газоподібних речовин, що приймають участь у процесі перетворення. Теплова енергія перетворення системи при цьому дорівнює зміні ентальпії, тобто
Теплові ефекти хімічних реакцій. Закон Гесса. Хімічні процеси завжди супроводжуються виділенням або поглинанням теплоти. Кількість тепла, що виділяється чи поглинається при протіканні даної хімічної реакції, називається тепловим ефектом даної хімічної реакції. Так як більшість хімічних реакцій і практично всі біохімічні реакції протікають при постійному тиску, на основі першого закону термодинаміки теплові ефекти хімічних реакцій характеризуються зміною ентальпії. Якщо для реакції утворення хлориду амоніаку зміна ентальпії від'ємна (екзотермічний процес) таке термохімічне рівняння має вигляд:
Для реакції утворення гідрогенхлориду (ендотермічний процес) реакція описується рівнянням:
На величину теплових ефектів хімічних реакцій впливають наступні фактори: агрегатний стан реагуючих речовин, їх природа, кількість реагуючих речовин, умови проведення реакції (P = const, V = const). Для порівняння теплових ефектів їх приводять до однакових умов. З цією метою введено поняття стандартних ефектів, значення яких вимірюють при T = 298 K і P = 101,325 кПа. Стандартні теплові ефекти позначають Оскільки ентальпія залежить від стану речовин, то в термохімічних рівняннях обов'язково позначають їх стан: г - газ, т - тверде тіло, к - кристал тощо.
Для розрахунку теплових ефектів реакцій, які експериментально визначити немає можливості, застосовують закон Гесса: тепловий ефект процесу не залежить від шляхів переходу або проміжних стадій, а визначається лише початковим і кінцевим станами системи. Наприклад, водний розчин хлориду амоніаку може бути утворений з амоніаку, гідрогенхлориду і рідкої води за двома шляхами (рис.1.3).
1) 2) 3) 4) 5) Як видно з рис.1.3, на якому схематично представлені обидва процеси і показані відповідні теплові ефекти, сумарний тепловий ефект за I шляхом дорівнює – 90,77 кДж, а тепловий ефект другого процесу (II) складає – 90,74 кДж, тобто практично співпадають. Таким чином:
Закон Гесса справедливий для ізохорних та ізобарних процесів. На його основі розраховують теплові ефекти більшості біохімічних процесів (теплові ефекти таких реакцій експериментально визначити неможливо). Для таких підрахунків використовують табличні дані теплот утворення ( Теплота утворення хімічної сполуки – це кількість тепла, що поглинається або виділяється при утворенні одного моля цієї сполуки із простих речовин при стандартних умовах. Теплоту утворення простих речовин умовно приймають рівною нулю. Якщо утворення сполук відбувається з виділенням тепла такі сполуки стійкі при звичайних умовах, а якщо речовини утворюються з поглинанням тепла – нестійкі. Теплота згоряння хімічної речовини - це кількість тепла, що виділяється при згорянні одного моля даної речовини в чистому Оксигену (кисні) за даних умов (P, T), до вищих оксидів елементів, які входять до складу речовини. Для виконання термохімічних розрахунків використовують наслідки із закону Гесса. I – й наслідок. Тепловий ефект хімічної реакції рівний сумі теплот утворення продуктів реакції мінус сума теплот утворення вихідних речовин з врахуванням стехіометричних коефіцієнтів
II – й наслідок. Тепловий ефект реакції рівний сумі теплот згоряння вихідних речовин мінус сума теплот згоряння продуктів реакції з врахуванням стехіометричних коефіцієнтів
III – й наслідок. Тепловий ефект розкладу будь-якої речовини рівний за величиною і протилежний за знаком тепловому ефекту її утворення
IV – й наслідок. Якщо здійснюються дві реакції, які приводять із різних початкових станів до однакових кінцевих, то різниця між тепловими ефектами першої і другої реакцій є тепловим ефектом переходу першого початкового стану в другий. V – й наслідок. Якщо здійснювати дві реакції, які приводять із однакових початкових станів до різних кінцевих, то різниця між тепловим ефектом першої і другої реакцій є тепловим ефектом переходу другого кінцевого стану в перший. Теплоти утворення більшості сполук отримують шляхом розрахунку за законом Гесса із інших термохімічних величин. Так, наприклад, теплота утворення бензену
може бути розрахована, якщо відомі теплоти згоряння бензену, Карбону (графіту), і Гідрогену
За законом Гесса маємо:
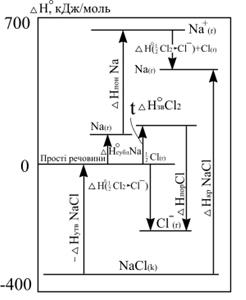
В ряді випадків теплоту утворення хімічних сполук визначають не з простих речовин, а із атомів (атомна теплота утворення). Для розрахунку атомної теплоти утворення враховують теплоту сублімації твердої речовини і теплоту дисоціації молекул газоподібних речовин на атоми. Як приклад розглянемо спосіб розрахунку енергії кристалічної решітки для кристалічного натрій хлориду. Кристалічний натрій хлорид при стандартних умовах може розкладатися на прості речовини і переходити в газоподібний стан (сублімація).
Також, відбувається дисоціація молекулярного газоподібного хлору
і йонізація атомів натрію і хлору
Таким чином з кристалічним NaCl відбувається процес:
Подальший перебіг газоподібних йонів натрію і хлору замикає термодинамічний цикл (рис.1.4) (цикл Борна-Габера). Виходячи з того, що сумарна зміна ентальпії в циклі дорівнює нулю, маємо:
Енергію кристалічної решітки можна розрахувати за універсальним рівнянням А.Ф.Капустінського
де Sn – число йонів в молекулі, Z – валентність йонів, ra i rk – йонні радіуси аніона і катіона для координаційного числа 6. Залежність теплових ефектів хімічних реакцій від температури. З врахуванням молярних ізохорних та ізобарних теплоємностей (СV, CP) температурна залежність теплових ефектів за законом Кірхгофа виражається рівняннями:
де
Для точних розрахунків враховують температурну залежність теплоємності:
Коефіцієнти а, в, с, d, с¢ подаються в довідковій літературі. Оскільки в літературі подаються значення коефіцієнтів для СР, то якщо необхідно визначити значення теплового ефекту DU при сталому об¢ємі, враховують що для твердих тіл:
А для газів
Тепловий ефект при будь-якої температурі розраховують користуючись тепловим ефектом реакції, виміряним за стандартних умов:
Можливий розрахунок теплових ефектів з використанням середніх значень теплоємностей в інтервалі температури 298 – Т:
Розрахунок теплових ефектів при наявності фазових перетворень в інтервалі температур 298 – Т проводять за рівнянням:
де СР¢ і СР² - теплоємності фаз, стійких у даному інтервалі температур. Фазові перетворення супроводжуються поглинанням або виділенням прихованої теплоти перетворення Для визначення прихованих теплот перетворення необхідно враховувати вплив агрегатного стану компонентів реакції (рис.1.5). В даному випадку реакція відбувається між речовинами, що перебувають у рідкому стані (процес 1- 4). Враховуючи, що ентальпія є функція стану, маємо:
де
При врахуванні фазових перетворень застосовують рівняння у такому вигляді:
Наприклад, розглядаючи процес утворення карбіду бору, що відбувається при температурі 1800 К за реакцією:
при якому плавляться магній (723 К) і бор оксид (923 К), випаровується магній (1390 К), тепловий ефект реакції за рівнянням виразиться як:
Другий закон термодинаміки. Ентропія. В природі всі фізичні, хімічні і біологічні перетворення здійснюються у певному напрямку і до певної межі. Усі ці перетворення відбуваються довільно. Вони є термодинамічно незворотні, так як завжди є втрати енергії системою в навколишнє середовище у вигляді тепла, тертя, випромінювання. Незворотні термодинамічні процеси можуть бути двох типів: несамовільні і самовільні. Для здійснення перших необхідно прикласти енергію ззовні, другі – відбуваються без витрати енергії зовні. Напрямок проходження самовільних процесів встановлює другий закон термодинаміки: - самовільно можуть відбуватися тільки ті процеси, при яких система переходить в найбільш імовірний стан; - теплота не може самовільно переходити від тіла з меншою температурою до тіла з більшою температурою; - різні види енергії прагнуть перейти в теплоту, а теплота прагне рівномірно розподілитись між всіма тілами. Напрямок, в якому самовільно відбувається хімічна реакція, визначається сумісною дією двох факторів: 1) тенденцією до переходу системи в стан з найменшою внутрішньою енергією (для ізобарних процесів – з найменшою ентальпією); 2) тенденцією до досягнення імовірного стану (W), тобто стану, який може бути реалізований найбільшим числом рівномірних мікростанів. Мірою імовірності стану системи в термодинаміці прийнято ентропію – S, величину пропорційну логарифму числа рівномірних мікростанів, якими може бути реалізований даний макростан:
де k – стала Больцмана Ентропія є мірою безпорядку в системі, мірою хаотичності розміщення частинок в речовині або тіл в системі. Вона характеризує ту частину енергії в незворотних процесах, яка не перетворюється в роботу, а розсіюється в навколишнє середовище у вигляді теплоти. На величину ентропії речовин впливає їх природа і кількість (з ростом частинок ентропія зростає), а також умови, в яких находяться речовини (тиск, об'єм, температура, агрегатний стан). Значення абсолютної ентропії речовин розраховують при стандартних умовах (р = 101,325 кПа, Т = 298 К, t = 250С) і позначають Прийнято рахувати, що при 0 К ентропія речовини дорівнює нулю, оскільки при цій температурі розміщення атомів або молекул в кристалічній структурі характеризується максимальним порядком. З підвищенням температури ентропія завжди зростає. Вона стрибкоподібно збільшується при послідовному переході речовини з твердого кристалічного стану у газоподібний стан. На рис.1.6 приведена типова крива зміни ентропії речовини при її нагріванні. Відрізок ОА характеризує поступове збільшення значень ентропії від 0 до температури плавлення (ТПЛ). В точці плавлення А відбувається стрибок ентропії (відрізок АВ) на ΔSПЛ. Відрізок ВС характеризує збільшення значень ентропії при нагріванні рідкої речовини від температури кипіння (ТКИП). В точці кипіння С також відбувається стрибок ентропії (відрізок СD) на ΔSВИП. Стрибкоподібна зміна ентропії в точках плавлення і кипіння відбувається при постійній температурі. При подальшому нагріванні (крива DE) ентропія газоподібної речовини знов плавно зростає.
В разі збільшення тиску в системі або при охолодженні зміна ентропії відбувається в зворотному напрямку, яка характеризується кривими ЕD, СВ і АО. При цьому в точках D (початок конденсації) і В (початок кристалізації) спостерігається стрибкоподібне зменшення значень ентропії при сталих температурах. Зміна значень ентропії в процесах конденсації (ΔSКОНД) і кристалізації (ΔSКР) дорівнює значенням ΔSКИП і ΔSПЛ відповідно. Ентропія як функція системи підкоряється закону Гесса. Це можна довести розглядаючи процеси переходу води із одного стану в інший. Так процес переходу льоду у пару можливий за двома шляхами. Перший – через плавлення і випаровування рідини. В цьому випадку зміна ентропії складає:
Другий шлях – безпосередній перехід молекул води із льоду в пару – сублімація (возгонка). Зміна ентропії сублімації дорівнює:
З наведеного випливає, що зміна ентропії складного процесу, дорівнює сумі змін ентропії кожної окремої стадії цього процесу:
Наприклад, якщо переохолоджений лід при температурі -100 С поступово нагрівати до перетворення його у пару з температурою 1200 С загальна зміна ентропії буде дорівнювати сумі змін ентропії таких стадій: 1) нагрівання льоду від –10 до 00 С, ΔS1; 2) плавлення льоду, ΔSПЛ; 3) нагрівання води від 0 до температури кипіння 1000 С, ΔS2; 4) випаровування води, ΔSВИП; 5) нагрівання пари від 100 до 1200 С, ΔS3. За другим законом термодинаміки при нагріванні системи (абсолютна ентропія) чисельно дорівнює:
де С - молярна теплоємність речовини. Використовуючи значення стандартної ентропії визначають абсолютну ентропію при будь-якій температурі за рівнянням:
Загальний вираз для розрахунку температурної залежності ентропії речовини, що знаходиться в стандартному стані і характеризується фазовими переходами, має вигляд:
Для хімічної реакції, що відбувається при температурі Т, зміна ентропії хімічного процесу дорівнює різниці абсолютних ентропій продуктів реакції і вихідних речовин:
Енергія Гібсса. Напрямок хімічної реакції. Узагальнені рівняння першого і другого законів термодинаміки (співвідношення Максвела) відображають зв'язок між ентропією і параметрами стану системи (тиск, температура, об'єм). Характеристичними функціями, виведеними на підставі співвідношень Максвела, є енергія Гіббса (ізобарно-ізотермічний потенціал):
і енергія Гельмгольца (ізохорно-ізотермічний потенціал):
Ізобарний і ізохорний потенціали є функціями стану системи і їх використовують для визначення напрямку процесу в умовах термодинамічної рівноваги. Перебіг самочинного процесу в неізольованій системі можливий лише в напрямку, при якому за умов Т=const, Р=const зменшується енергія Гіббса і за умов Т=const, V=const зменшується енергія Гельмгольца, тобто ΔG < 0 і ΔF < 0. Якщо ΔG > 0 і ΔF > 0 зміна стану системи відбувається тільки при використанні зовнішньої роботи. У випадку коли ΔG і ΔF дорівнюють нулю, то система перебуває у рівновазі. Зміну енергії Гіббса в хімічній реакції розраховують за рівнянням Гіббса – Гельмгольца:
В цьому рівнянні
В температурному інтервалі 298 – Т враховується температурна залежність ΔG˚Т = f(Т) у вигляді рівності:
Рівняння (1.41) вирішується методом розкриття інтегралів:
Можливе виключення інтегральних величин Δс’/Т або Δb·Т+ Δс’/Т2, що спрощує розрахунок, але при цьому точність розрахунку зменшується. З рівняння Гіббса-Гельмгольца випливає: 1) якщо ΔН < 0 і ΔS > 0 то завжди ΔG < 0, тобто реакція з виділенням теплоти і збільшенням степені невпорядкованості можлива при всіх температурах; 2) якщо ΔH > 0 і ΔS < 0, то завжди ΔG > 0, тобто реакція з поглинанням теплоти і збільшенням степені упорядкованості неможлива ні при яких умовах; 3) у рештах випадках (ΔН < 0, ΔS < 0 і ΔН >0, ΔS > 0) знак ΔG залежить від співвідношення членів ΔН і ТΔS. Реакція можлива, тільки якщо вона супроводжується зменшенням ізобарного потенціалу; 4) при кімнатній температурі, коли значення Т невелике, значення добутку ТΔS також невелике (рис.1.8), і звичайно зміна ентальпії переважує ТΔS. Тому більшість реакцій, які відбуваються при кімнатній температурі, - це реакції з виділенням теплоти (ΔН < 0). При збільшенні температури збільшується і добуток ТΔS, тому при високих температурах навіть реакції з поглинанням теплоти (ΔН > 0) стають самовільними.
Слід відмітити, що хімічні реакції, під час перебігу яких відбувається зменшення термодинамічних потенціалів, називають екзергонічними, а якщо потенціали зростають – ендергонічними. При ізохорному процесі самовільна реакція можлива тільки при ΔF < 0. Для ΔF тлумачення точно такі, як і для ΔG. Чисельно ΔG і ΔF відрізняються на роботу розширення. Зв'язок між основними термодинамічними функціями ілюструє діаграма, що зображена на рисунку:
З аналізу співвідношень витікає, що: при Т→ 0 і Р → 0 ∆G → ∆F, а при Т = 0, Р = 0 і ∆n = 0 ∆G = ∆F. Крім того, чим більше ∆n і тиск в реакційній системі, тим більше чисельне значення роботи розширення. В табл. 1.1. співставлені форми характеристичних функцій, їх зміна при одному постійному параметрі стану і сумарні інтегральні форми. Таблиця 1.1 Характеристичні функції і їх перемінні
продовження табл. 1.1
Теплота фазових перетворень. Залежність теплоти фазового перетворення від умов його проходження для будь-якого рівноважного процесу визначається за рівнянням Клаузіуса – Клапейрона:
де НФ.П. – теплота фазового перетворення (плавлення, випаровування, поліморфного перетворення, сублімації тощо); ∆V – зміна об'єму при фазовому переході, dp/dT – похідна, що зв'язує зміну температури і тиску за умови збереження стану рівноваги між фазами. Теплота плавлення – переходу твердої фази в рідку - завжди позитивна. Об'єм рідкої фази (VР) в загальному випадку може бути більше або менше об'єму в тій же кількості твердої фази (VТ). Звідси витікає, що величина dp/dТ, яка характеризує зміну температури від тиску, може бути позитивною або від'ємною тобто, температура плавлення може підвищуватись або знижуватись зі збільшенням тиску. Величина dТ/dР має від'ємне значення лише для води і деяких інших речовин, у яких густина рідини при температурі плавлення більше густини твердої фази. Рівняння Клаузіуса-Клапейрона в цьому випадку набуває вигляду:
При випаровуванні – переходу рідкої фази в газоподібну – теплота випаровування також позитивна, а температура випаровування завжди підвищується зі зростанням тиску. В зв'язку з тим, що мольний об'єм пари значно перевищує мольний об'єм рідини значення Vр в рівнянні можна знехтувати і воно прийме вигляд:
Якщо насичену пару рахувати ідеальним газом, тобто
Тоді рівняння (1.44) набуде вигляду:
В області невисоких тисків теплоти випаровування порівняно мало змінюється з температурою, тому її можна вважати сталою. В цьому випадку після перетворення цього рівняння дістанемо рівняння:
які широко застосовуються в практиці. Практичне застосування термодинамічних розрахунків. Розглянемо розрахунок основних термодинамічних величин на прикладі хімічної реакції, яка відбувається в гомогенній системі:
при температурі 2000 К і тиску 3 атмосфери. З довідника виписуємо термодинамічні величини для вихідних сполук і продуктів реакції.
|

 (1.1)
(1.1) (1.2)
(1.2) Рис.1.1. Якісна характеристика залежності зміни ентальпії від температури
Рис.1.1. Якісна характеристика залежності зміни ентальпії від температури

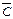 визначають з виразу:
визначають з виразу: (1.3)
(1.3)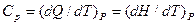 (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6)
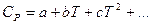 , (1.8)
, (1.8) , (1.9)
, (1.9) (1.10)
(1.10)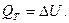 (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) (1.15)
(1.15)

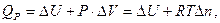 (1.16)
(1.16) (1.17)
(1.17) .
.

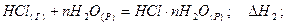
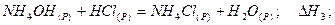
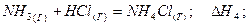


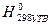 .) і теплот згоряння (
.) і теплот згоряння (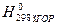 ) речовин.
) речовин.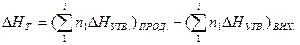 . (1.18)
. (1.18)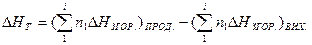 .
.  (1.19)
(1.19) . (1.20)
. (1.20)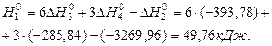
 ,
,
 .
.


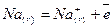 ;
;
 ,
,

 .
.
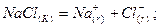
 .
.

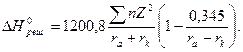
 (1.22)
(1.22)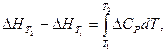 (1.23)
(1.23) (1.24)
(1.24)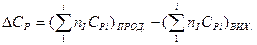 . (1.25)
. (1.25) (1.26)
(1.26)
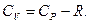 (1.27)
(1.27) (1.28)
(1.28)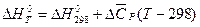 . (1.29)
. (1.29) (1.30)
(1.30)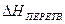 .
.

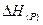
 1 2
T = const; P = const;
1 2
T = const; P = const;
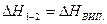 4 3
Конденсування
(Р, Т)
4 3
Конденсування
(Р, Т)
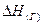


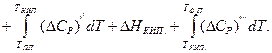 (1.31)
(1.31)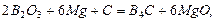


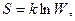 (1.32)
(1.32) ,
,  - стала Авогадро.
- стала Авогадро. (стандартна ентропія). Розмірність
(стандартна ентропія). Розмірність 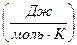 .
.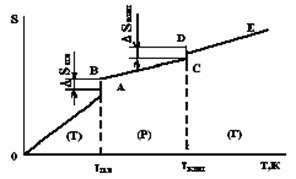

 Отже, зміна ентропії, як і зміна ентальпії, не залежить від способу переходу, при умові, що вихідний і кінцевий стани речовини однакові. Це ілюструє рис.1.7 на якому показані зміни ентропії і ентальпії води при фазових переходах.
Отже, зміна ентропії, як і зміна ентальпії, не залежить від способу переходу, при умові, що вихідний і кінцевий стани речовини однакові. Це ілюструє рис.1.7 на якому показані зміни ентропії і ентальпії води при фазових переходах.
 (1.33)
(1.33) (1.34)
(1.34)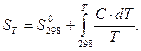 (1.35)
(1.35)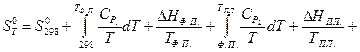
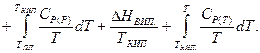 (1.36)
(1.36)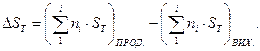 (1.37)
(1.37) (1.38)
(1.38) (1.39)
(1.39) (1.40)
(1.40)


 (1.41)
(1.41)
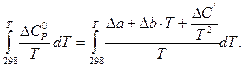


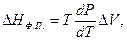 (1.42)
(1.42)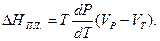 (1.43)
(1.43)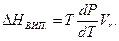 (1.44)
(1.44)
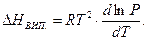 (1.45)
(1.45)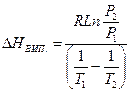
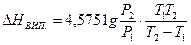 (1.46)
(1.46)


