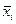Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ отсчёта средней от условного 0. Способ моментов.Содержание книги
Поиск на нашем сайте
Задача. Определить средний вес сотни писем, используя способ моментов или условного 0. Таб.1: Исходные данные
i – интервал → i = 100 А – соответствует xi при наибольшей частоте (max f)→ A = 900
Вывод: средний вес сотни писем равен 926 гр. Показатели вариации Меры вариации – абсолютные и относительные показатели вариации. Абсолютные показатели вариации: 1) Размах вариации: 2) Среднее линейное отклонение: Относительные показатели вариации: 1) Коэффициент осцилляции: 2) Коэффициент вариации: Если Если Если
3) Линейный коэффициент вариации: 4) Дисперсия 5) Среднее квадратическое отклонение: Структурные средние: 1) Мода: x0 – нижняя граница модального ряда i - интервал 2) Медиана: Задача. По приведённым в таблице данным определить: 1) среднюю заработную плату одного работника, 2) моду и медиану, 3) показатели вариации, 4) коэффициенты асимметрии и эксцесса. Изобразить анализируемый ряд графически (+моду и медиану) и сформулировать выводы. 1) Средняя з/п: 2) Мода: Медиана: Таб.1: Исходные данные
i = 60 A = 390 3)
Рис.1 Гистограмма распределения численности работников по размеру заработной платы.
Рис.2 Кумулята распределения численности работников по размеру заработной платы.
4) 1) Асимметрия – смещение закона распределения. 2) Эксцесс определяет "остриё" вершины (островершинная, плосковершинная)
Коэффициент асимметрии Пирсона:
Ка > 0 → асимметрия правосторонняя Ка < 0 → асимметрия левосторонняя Ка = 0 → закон распределения имеет нормальный вид
Характеристика правосторонней асимметрии: M0 < Me < Характеристика левосторонней асимметрии:
Коэффициент асимметрии As определяет величину смещения фактической кривой относительно нормальной.
As > 0,5 → значительное смещение кривой As < 0,25 → незначительное смещение кривой As = 0 → рассчитанная кривая совпадает с фактической Эксцесс:
Дисперсия 4 способа расчёта дисперсии: 1) Традиционный: 2) Условного 0: 3) Моментов: 4) Разности средней квадратов и квадрата средней:
Определение дисперсии при 2х и более группировках: 1) Внутригрупповая дисперсия: для дискретных величин: 2) Средняя из внутригрупповых дисперсий: 3) Межгрупповая дисперсия: 4) Общая дисперсия:
Характеристики дисперсии: 1) Коэффициент детерминации: показывает какая доля всей вариации признака обусловлена признаком, положенным в основание группировок. 2) Корреляционное отношение (эмпирическое): показывает тесноту связей между группировочным и результативным признаками.
Задача. Дано распределение численности работников по уровню выработки (производительности труда) в 2х филиалах организации связи. Рассчитать все виды дисперсии и характеристики дисперсии. Таб.1: Исходные данные
По традиционной формуле:
Разбивка предприятий на филиалы слабо влияет на уровень выработки. Показатель вариации:
Задача. По исходным данным определить все виды дисперсии. Таб.1: Исходные данные
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.160.29 (0.01 с.) |



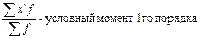

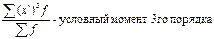

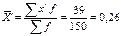


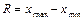



 < 33%, то совокупность однородная и её можно подвергать анализу
< 33%, то совокупность однородная и её можно подвергать анализу

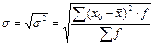

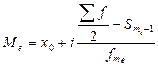


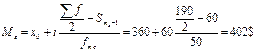
 |f
|f






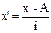

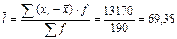
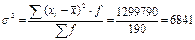

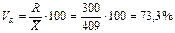
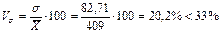
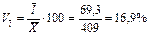



 1) 2)
1) 2)
 (380 < 402 < 409)
(380 < 402 < 409)
 - центральный момент 3его порядка
- центральный момент 3его порядка
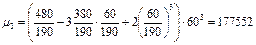
 < 0,25
< 0,25
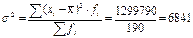
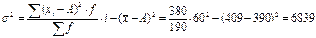

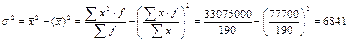



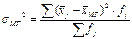
 - правило сложения дисперсий
- правило сложения дисперсий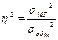
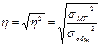
 xi
xi




 44,1
44,1
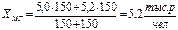 0,5
0,5

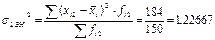

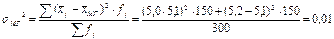


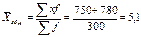
 Группировочным признаком обусловлено 0,82% всей вариации признака
Группировочным признаком обусловлено 0,82% всей вариации признака Доля межгрупповой вариации признака составляет 9,04% - очень слабая теснота связи.
Доля межгрупповой вариации признака составляет 9,04% - очень слабая теснота связи.