
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 1. Математика и психологияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос 1. МАТЕМАТИКА И ПСИХОЛОГИЯ Для существования психологии как науки она в своем научном становлении неизбежно должна была пройти и прошла путь математизации, хотя не во всех странах и не в полной мере. Точной даты начала пути математизации, пожалуй, не знает ни одна наука. По-видимому, И. Ф. Гербарту первому принадлежит мысль о том, что свойства потока сознания — это величины и, следовательно, они в дальнейшем развитии научной психологии подлежат измерению. Ему также принадлежит идея «порога сознания», и он первый употребил выражение «математическая психология». М.В.Дробиш издал в Лейпциге на немецком языке монографию под недвусмысленным названием: «Эмпирическая психология согласно естественнонаучному методу». В этой книге нет математики в смысле формул, символики и расчетов, но там есть четкая система понятий о характеристиках потока представлений в сознании как взаимосвязанных величинах. Математические средства для изучения сложных многомерных объектов, в том числе высших психических функции — интеллекта, способностей, личности, стали создавать англоязычные ученые. Среди других результатов оказалось, что рост потомков как бы стремится возвратиться к среднему росту предков. Появилось понятие «регрессия», и были получены уравнения, выражающие эту зависимость. Был усовершенствован коэффициент, раньше предложенный французом Бравэ. Этот коэффициент количественно выражает соотношение двух изменяющихся переменных, т. е. корреляцию. Чарльз Спирмен внес огромный вклад в развитие, он предложил теорию «генерального» фактора, определяющего совместную изменчивость переменных тестовых результатов, а также разработал метод выявления этого фактора по корреляционной матрице. Это был первый метод факторного анализа, созданный в психологии и для психологических целей. У однофакторной теории Ч. Спирмена быстро нашлись оппоненты. Противоположную, многофакторную теорию, объясняющую корреляции, предложил Леон Терстоун. Ему же принадлежит первый метод мультифакторного анализа, основанный на применении линейной алгебры. После Ч. Спирмена и Л. Терстоуна факторный анализ, не только стал одним из важнейших математических методов многомерного анализа данных в психологии, но и вышел далеко за ее пределы, превратился в общенаучный метод анализа, данных.
Созданный в области биологии Рональдом Фишером дисперсионный анализ становится основным математическим методом в генетической психологии. Математические модели из теории автоматического регулирования и шенноновская теория информации широко применяются в инженерной и общей психологии. В итоге современная научная психология во многих своих отраслях математизирована значительным образом. Многие методы играют служебную роль в самой математике, как, в частности, доказательства теорем или определенные строгости изложения, так приветствуемые математиками. Для практических приложений математических методов за пределами математики, в том числе в психологии, математические строгости и тонкости не нужны: они затеняют суть результатов, в которых математика должна находиться на заднем плане, как, например, логарифмическая основа психофизического закона Вебера—Фехнера.
Вопрос 2. ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ. Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность — это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, женщины 10-89 лет, использующие крем для рук определённой марки не реже одного раза в неделю, и имеющие доход не ниже 5 тысяч рублей на одного члена семьи. Выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании. Характеристики выборки:
Необходимость выборки
Вопрос 4. ТАБЛИЦЫ И ГРАФИКИ. ОСНОВНЫЕ СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ. Таблица – это рациональное изображение цифрового материала, полученного в результате статистического наблюдения. Таблица состоит из 1) макета, 2) цифрового материала. Макет – заголовочная часть, отделяется жирными линиями, остаточная часть – хвост, котор в свою очередь делится на боковик (первую слева графу) и прографку (остальные части таблицы). Каждая таблица состоит из 2х элементов – подлежащего и сказуемого. Подлежащее – это то, о чём говорится в данной таблице (объект исследования). Подлежащее записывается слева в таблице по строкам. Сказуемое – это то, что говорится о подлежащем. Сказуемое записывается справа в графах. В зависимости от построения подлежащего и сказуемого различают простые и сложные таблицы. Простая таблица – подлежащее которой не о группировано. Это таблица подлежащее которой содержит перечень единиц наблюдения (перечневая таблица), хронологических дат (хронолог таблица) или территориальных подразделений (территориальная таблица) Такие таблицы имеют чисто описательный характер. Их задача показать существенные типы явлений. графического образа поля графика пространственных и масштабных ориентиров экспликации графика. Полем графика является место, на котором он выполняется. Графический образ — это символические знаки, с помощью которых изображаются статистические данные (линии, точки, прямоугольники, квадраты, круги и т.д.). Пространственные ориентиры определяют размещение графических образов. Масштабные ориентиры придают этим образам количественную определенность. Вводятся ось абсцисс и ось ординат, как правило, используется равномерная линейная шкала и на осях откладываются масштабы. Экспликация графика — это пояснение его содержания, включает в себя заголовок графика, объяснения масштабных шкал, условные обозначения. Графики различают в соответствии с 2 признаками: 1) графические образы, 2) задачи, решаемые с помощью графика. Графические образы выбираются в зависимости от цели, поставленной перед графиком. В зависимости от графического образа различают виды графиков: точечные, линейные, полосовые, столбиковые, квадратные, круговые, секторные, прямоугольные, фигурные. Графики важны не только для придания наглядности, но и имеют большое аналитическое значение. Посредством графиков выявляются качественные особенности и тенденции в развитии явлений, изучается структура и динамика сложных совокупностей, устанавливается теснота связей между признаками, обнаруживаются ошибки в статистических материалах.
ВЫБОРОЧНОЕ СРЕДНЕЕ Выборочное среднее значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.
Выборочное среднее определяется при помощи следующей формулы:
где хср —выборочная средняя величина или среднее арифметическое значение по выборке; п — количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина; xk — частные значения показателей у отдельных испытуемых. Всего таких показателей п, поэтому индекс k данной переменной принимает значения от 1 до п; ∑ — принятый в математике знак суммирования величин тех переменных, которые находятся справа от этого знака. Выражение Пример. Допустим, что в результате применения психодиагностической методики для оценки некоторого психологического свойства у десяти испытуемых мы получили следующие частные показатели степени развитости данного свойства у отдельных испытуемых: х1= 5, х2 = 4, х3 = 5, х4 = 6, х5 = 7, х6 = 3, х7 = 6, х8= 2, х9= 8, х10 = 4. Следовательно, п = 10, а индекс k меняет свои значения от 1 до 10 в приведенной выше формуле. Для данной выборки среднее значение, вычисленное по этой формуле, будет равно:
ДИСПЕРСИЯ Дисперсия как статистическая, величина характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения или разброс данных. Прежде чем представлять формулу для расчетов дисперсии, рассмотрим пример. Воспользуемся теми первичными данными, которые были приведены ранее и на основе которых вычислялась в предыдущем примере средняя величина. Мы видим, что все они разные и отличаются не только друг от друга, но и от средней величины. Меру их общего отличия от средней величины и характеризует дисперсия. Ее определяют для того, чтобы можно было отличать друг от друга величины, имеющие одинаковую среднюю, но разный разброс. Представим себе другую, отличную от предыдущей выборку первичных значений, например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко убедиться в том, что ее средняя величина также равна 5,0. Но в данной выборке ее отдельные частные значения отличаются от средней гораздо меньше, чем в первой выборке. Выразим степень этого отличия при помощи дисперсии, которая определяется по следующей формуле:
где
п — количество испытуемых в выборке или первичных значений, по которым вычисляется дисперсия.
Определим дисперсии для двух приведенных выше выборок частных значений, обозначив эти дисперсии соответственно индексами 1 и 2:
Мы видим, что дисперсия по второй выборке (0,4) значительно меньше дисперсии по первой выборке (3,0). Если бы не было дисперсии, то мы не в состоянии были бы различить данные выборки.
ВЫБОРОЧНОЕ ОТКЛОНЕНИЕ
Иногда вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую выборочное отклонение. Оно равно квадратному корню, извлекаемому из дисперсии, и обозначается тем же самым знаком, что и дисперсия, только без квадрата—
МЕДИАНА Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Например, для выборки 2, 3,4, 4, 5, 6, 8, 7, 9 медианой будет значение 5, так как слева и справа от него остается по четыре показателя. Если ряд включает в себя четное число признаков, то медианой будет среднее, взятое как полусумма величин двух центральных значений ряда. Для следующего ряда 0, 1, 1, 2, 3, 4, 5, 5, 6, 7 медиана будет равна 3,5. Знание медианы полезно для того, чтобы установить, является ли распределение частных значений изученного признака симметричным и приближающимся к так называемому нормальному распределению. Средняя и медиана для нормального распределения обычно совпадают или очень мало отличаются друг от друга. Если выборочное распределение признаков нормально, то к нему можно применять методы вторичных статистических расчетов, основанные на нормальном распределении данных. В противном случае этого делать нельзя, так как в расчеты могут вкрасться серьезные ошибки. Если в книге по математической статистике, где описывается тот или иной метод статистической обработки, имеются указания на то, что его можно применять только к нормальному или близкому к нему распределению признаков, то необходимо неукоснительно следовать этому правилу и полученное эмпирическое распределение признаков проверять на нормальность. Если такого указания нет, то статистика применима к любому распределению признаков. МОДА Мода еще одна элементарная математическая статистика и характеристика распределения опытных данных. Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке. На графиках, представленных на рис. 72, моде соответствуют самые верхние точки кривых, вернее, те значения этих точек, которые располагаются на горизонтальной оси.
Для симметричных распределений признаков, в том числе для нормального распределения, значения моды совпадают со значениям среднего и медианы. Для других типов распределений, несимметричных, это не характерно. К примеру, в последовательности значений признаков 1, 2, 5, 2, 4, 2, 6, 7, 2 модой является значение 2, так как оно встречается чаще других значений — четыре раза. ИНТЕРВАЛ Иногда исходных частных первичных данных, которые подлежат статистической обработке, бывает довольно много, и они требуют проведения огромного количества элементарных арифметических операций. Для того чтобы сократить их число и вместе с тем сохранить нужную точность расчетов, иногда прибегают к замене исходной выборки частных эмпирических данных на интервалы. Интервалом называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. Пример. Представим следующий ряд частных признаков: О, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 8, 8, 8, 9, 9, 9, 10, 10, 11, 11, 11. Этот ряд включает в себя 30 значений. Разобьем представленный ряд на шесть подгрупп по пять признаков в каждом. *Первая подгруппа включит в себя первые пять цифр, *вторая — следующие пять и т.д. Вычислим средние значения для каждой из пяти образованных подгрупп чисел. Они соответственно будут равны 1,2; 3,4; 5,2; 6,8; 8,6; 10,6. Таким образом, нам удалось свести исходный ряд, включающий тридцать значений, к ряду, содержащему всего шесть значений и представленному средними величинами. Это и будет интервальный ряд, а проведенная процедура — разделением исходного ряда на интервалы. На практике, составляя интервальный ряд, рекомендуется руководствоваться следующим правилом: если в исходном ряду признаков больше чем тридцать, то этот ряд целесообразно разделить на пять-шесть интервалов и в дальнейшем работать только с ними. Для проверки сказанного проведем пробное вычисление среднего значения по приведенному выше ряду, составляющему тридцать чисел, и по ряду, включающему только интервальные средние значения. Полученные цифры с точностью до двух знаков после запятой будут соответственно равны 5,97 и 5,97, т.е. являются одинаковыми.
Направленные гипотезы H0: X1 не превышает Х2 H1: X1 превышает Х2 Ненаправленные гипотезы Параметрические критерии Критерии, включающие в формулу расчета параметры распределения, то есть средние и дисперсии (/-критерий Стьюдента, критерий F и др.) Непараметрические критерия Критерии, не включающие в формулу расчета параметров распределения и основанные на оперировании частотами или рангами (критерий Q Розенбаума, критерий Т Вилкоксона и др.) И те, и другие критерии имеют свои преимущества и недостатки. На основании нескольких руководств можно составить таблицу, позволяющую оценить возможности и ограничения тех и других (Рунион Р., 1982; McCall R., 1970; J.Greene, M.D'Olivera, 1989).
Таблица 1.1 Возможности и ограничения параметрических и непараметрических критериев ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют прямо оценить различия в средних, полученных в двух выборках (t - критерий Стьюдента). 2.Позволяют прямо оценить различия в дисперсиях (критерий Фишера). 3.Позволяют выявить тенденции изменения признака при переходе от условия к условию (дисперсионный однофакторный анализ), но лишь при условии нормального распределения признака. 4.Позволяют оценить взаимодействие двух и более факторов в их влиянии на изменения признака (двухфакторный дисперсионный анализ). 5.Экспериментальные данные должны отвечать двум, а иногда трем, условиям: а) значения признака измерены по интервальной шкале; б) распределение признака является нормальным; в) в дисперсионном анализе должно соблюдаться требование равенства дисперсий в ячейках комплекса. 6.Математические расчеты довольно сложны. 7.Если условия, перечисленные в п.5, выполняются, параметрические критерии оказываются несколько более НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б - более низкие значения признака (критерии Q, U, φ* и др.). 2.Позволяют оценить лишь различия в диапазонах вариативности признака (критерий φ*). 3.Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерии тенденций L и S). 4.Эта возможность отсутствует. 5.Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть представлены в любой шкале, начиная от шкалы наименований; б) распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения в) требование равенства дисперсий отсутствует. 6.Математические расчеты по большей части просты и занимают мало времени (за исключением критериев χ2 и λ).
Из Табл. 1.1 мы видим, что параметрические критерии могут оказаться несколько более мощными4, чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. С интервальной шкалой есть определенные проблемы (см. раздел "Шкалы измерения"). Лишь с некоторой натяжкой мы можем считать данные, представленные не в стандартизованных оценках, как интервальные. Кроме того, проверка распределения "на нормальность" требует достаточно сложных расчетов, результат которых заранее неизвестен (см. параграф 7.2). Может оказаться, что распределение признака отличается от нормального, и нам так или иначе все равно придется обратиться к непараметрическим критериям. 4 О понятии мощности критерия см. ниже.
Непараметрические критерии лишены всех этих ограничений и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном - с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту задачу может решить только дисперсионный двухфакторный анализ. Учитывая это, в настоящее руководство включены в основном непараметрические статистические критерии. В сумме они охватывают большую часть возможных задач сопоставления данных. Единственный параметрический метод, включенный в руководство - метод дисперсионного анализа, двухфакторный вариант которого ничем невозможно заменить.
ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют прямо оценить различия в средних, полученных в двух выборках (t - критерий Стьюдента). 6.Позволяют прямо оценить различия в дисперсиях (критерий Фишера). 7.Позволяют выявить тенденции изменения признака при переходе от условия к условию (дисперсионный 8.Позволяют оценить взаимодействие двух и более факторов в их влиянии на изменения признака (двухфакторный дисперсионный анализ). 9.Экспериментальные данные должны отвечать двум, а иногда трем, условиям: а) значения признака измерены по интервальной шкале; б) распределение признака является нормальным; в) в дисперсионном анализе должно соблюдаться требование равенства дисперсий в ячейках комплекса. 8.Математические расчеты довольно сложны. 9.Если условия, перечисленные в п.5, выполняются, параметрические критерии оказываются несколько более НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б - более низкие значения признака (критерии Q, U, φ* и др.). 2.Позволяют оценить лишь различия в диапазонах вариативности признака (критерий φ*). 3.Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерии тенденций L и S). 4.Эта возможность отсутствует. 5.Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть представлены в любой шкале, начиная от шкалы наименований; б) распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения в) требование равенства дисперсий отсутствует. 6.Математические расчеты по большей части просты и занимают мало времени (за исключением критериев χ2 и λ).
НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 1. Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б - более низкие значения признака (критерии Q, U, φ* и др.). 2.Позволяют оценить лишь различия в диапазонах вариативности признака (критерий φ*). 3.Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерии тенденций L и S). 4.Эта возможность отсутствует. 5.Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть представлены в любой шкале, начиная от шкалы наименований; б) распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения в) требование равенства дисперсий отсутствует. 6.Математические расчеты по большей части просты и занимают мало времени (за исключением критериев χ2 и λ). Выборки 3 выборки и более
n1, n2 ≥ 11, n1 или n2<11 n ≤ 10 c≤6 n ˃ 10 c ˃ 6
критерий критерий критерий тенденций критерий Q Розенбаума U Манна Уитни S Джонкира H Крускара Уолеса
Если различия не выявляются, то использовать угловое преобразование Фишера
Q - критерий Розенбаума Критерий используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой из выборок должно быть не менее 11 испытуемых. U - критерий Манна-Уитни Критерий предназначен для оценки различий между бвумя выборками по уровню какого-либо признака, количественного измеренного. Он позволяет выявлять различия между малыми выборками, когда n1, n2 >3 или n1=2, n2> 3 и является более мощным, чем критерий Розенбаума. Вопрос 1. МАТЕМАТИКА И ПСИХОЛОГИЯ Для существования психологии как науки она в своем научном становлении неизбежно должна была пройти и прошла путь математизации, хотя не во всех странах и не в полной мере. Точной даты начала пути математизации, пожалуй, не знает ни одна наука. По-видимому, И. Ф. Гербарту первому принадлежит мысль о том, что свойства потока сознания — это величины и, следовательно, они в дальнейшем развитии научной психологии подлежат измерению. Ему также принадлежит идея «порога сознания», и он первый употребил выражение «математическая психология». М.В.Дробиш издал в Лейпциге на немецком языке монографию под недвусмысленным названием: «Эмпирическая психология согласно естественнонаучному методу». В этой книге нет математики в смысле формул, символики и расчетов, но там есть четкая система понятий о характеристиках потока представлений в сознании как взаимосвязанных величинах. Математические средства для изучения сложных многомерных объектов, в том числе высших психических функции — интеллекта, способностей, личности, стали создавать англоязычные ученые. Среди других результатов оказалось, что рост потомков как бы стремится возвратиться к среднему росту предков. Появилось понятие «регрессия», и были получены уравнения, выражающие эту зависимость. Был усовершенствован коэффициент, раньше предложенный французом Бравэ. Этот коэффициент количественно выражает соотношение двух изменяющихся переменных, т. е. корреляцию. Чарльз Спирмен внес огромный вклад в развитие, он предложил теорию «генерального» фактора, определяющего совместную изменчивость переменных тестовых результатов, а также разработал метод выявления этого фактора по корреляционной матрице. Это был первый метод факторного анализа, созданный в психологии и для психологических целей. У однофакторной теории Ч. Спирмена быстро нашлись оппоненты. Противоположную, многофакторную теорию, объясняющую корреляции, предложил Леон Терстоун. Ему же принадлежит первый метод мультифакторного анализа, основанный на применении линейной алгебры. После Ч. Спирмена и Л. Терстоуна факторный анализ, не только стал одним из важнейших математических методов многомерного анализа данных в психологии, но и вышел далеко за ее пределы, превратился в общенаучный метод анализа, данных. Созданный в области биологии Рональдом Фишером дисперсионный анализ становится основным математическим методом в генетической психологии. Математические модели из теории автоматического регулирования и шенноновская теория информации широко применяются в инженерной и общей психологии. В итоге современная научная психология во многих своих отраслях математизирована значительным образом. Многие методы играют служебную роль в самой математике, как, в частности, доказательства теорем или определенные строгости изложения, так приветствуемые математиками. Для практических приложений математических методов за пределами математики, в том числе в психологии, математические строгости и тонкости не нужны: они затеняют суть результатов, в которых математика должна находиться на заднем плане, как, например, логарифмическая основа психофизического закона Вебера—Фехнера.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.42.190 (0.014 с.) |


 соответственно означает сумму всех х с индексом k от 1 до n.
соответственно означает сумму всех х с индексом k от 1 до n.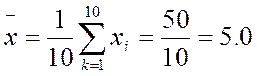

 — выборочная дисперсия, или просто дисперсия;
— выборочная дисперсия, или просто дисперсия; — выражение, означающее, что для всех xk от первого до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;
— выражение, означающее, что для всех xk от первого до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;









