
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет зубьев цилиндрических прямозубых колес на сопротивление контактной усталости (по контактным напряжениям). Вывод расчетной зависимости и ее анализ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчет на контактную прочность включает расчеты на сопротивление усталости и на предотвращение разрушения рабочих поверхностей зубьев при максимальной однократной нагрузке. Расчет на сопротивление усталости. Разрушение от переменных контактных напряжений начинается вблизи полюса. Поэтому расчетные напряжения определяют на линии контакта, проходящей через полюс П. Цель расчета — определение размеров передачи при выбранном материале и заданной твердости поверхности зубьев колес, при которых не будет прогрессивного выкрашивания. Условие контактной прочности записывают в виде
где σн — расчетное напряжение, зависящее от геометрических параметров передачи и нагрузки; [σ]н — допускаемое напряжение, зависящее от материала, термообработки колес и характера нагрузки. Контакт двух зубьев можно рассматривать как контакт двух цилиндров с радиусами кривизны ρ1 = N1П и ρ2 = N2П в полюсе зацепления П. В качестве исходной принимают формулу Герца для наибольших контактных напряжений σн на площадке контакта двух стальных цилиндров при их сжатии
Где Для получения расчетной зависимости в удобной форме заменим величины, входящие в формулу Герца через параметры зацепления. Для прямозубой передачи нормальная результирующая сила определяется через окружную силу Ft
Суммарная длина контактных линий К1К2 в прямозубой передаче переменна. В зоне однопарного зацепления она равна b, в зоне двухпарного зацепления — 2b. Для расчетов принимают
Для стальных колес модуль упругости Е = 2,1 • 105 МПа, тогда коэффициент, учитывающий механические свойства материала колес, ZЕ = 191,6 МПа0,5.
Учитывая
Подставим все в формулу Герца
Дополнительно обозначим
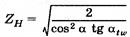
ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев.
Выразим
Для передач без смещения
39. Расчет зубьев цилиндрических прямозубых колес на изгибную усталость. Вывод расчетной зависимости на изгибную усталость. (Вывод формулы для расчета цилиндрических колес на изгиб).
Расчет зубьев на сопротивление усталости при изгибе основан на сопоставлении расчетного местного напряжения σF и допускаемого напряжения [σ] F. Расчетом определяют напряжения в опасном сечении на переходной поверхности зуба для шестерни и колеса раздельно. Зуб прямозубой передачи рассматривают как консольную балку с нагрузкой, распределенной по линии контакта зубьев. Силы трения малы, и их не учитывают. Нагрузку заменяют силой F, направленной по линии зацепления, касательной к основным окружностям. В расчетах рассматривают наиболее опасный случай, при котором полная нагрузка приложена к вершине зуба. Это возможно из-за ошибок изготовления или при коэффициенте перекрытия, близком к единице. Результирующая сила, приложенная к вершине, переносится на ось зуба и раскладывается на окружную и радиальную силы.
Находим напряжения от изгиба и сжатия в опасном сечении зуба:
где sx — толщина зуба в опасном сечении; b — ширина зубчатого колеса. На стороне сжатия результирующие напряжения больше, чем на стороне растяжения зуба. Однако образование трещин усталости и разрушение начинается на стороне растяжения. Поэтому расчет ведут по напряжениям
Выразим толщины и высоты зуба в долях модуля,
Для косозубых и шевронных передач, по сравнению с прямозубыми, характерно повышенное сопротивление усталости при изгибе, их дополняют еще двумя коэффициентами:
|
|||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.197 (0.01 с.) |


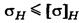 .
.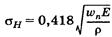
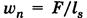 — распределенная нагрузка; F — нормальная к контактирующим поверхностям сила сжатия; ls, — суммарная длина контактных линий; Е — модуль упругости; ρ — приведенный радиус кривизны.
— распределенная нагрузка; F — нормальная к контактирующим поверхностям сила сжатия; ls, — суммарная длина контактных линий; Е — модуль упругости; ρ — приведенный радиус кривизны.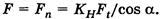
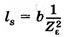 ,
, 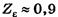 - коэффициент, учитывающий суммарную длину контактных линий.
- коэффициент, учитывающий суммарную длину контактных линий.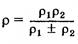
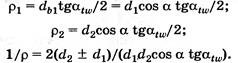
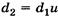 , получаем в итоге
, получаем в итоге
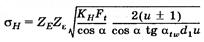
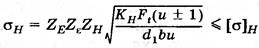
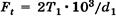 и заменим
и заменим 
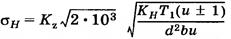
 .
. - коэффициент относительной ширины колеса.
- коэффициент относительной ширины колеса.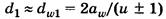

 =450 для прямозубых,
=450 для прямозубых, 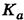 =410 для косозубых.
=410 для косозубых.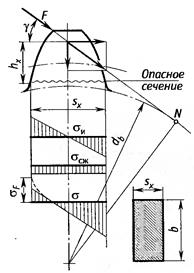
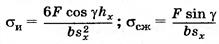
 .
.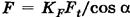 , KF – коэффициент нагрузки, получим
, KF – коэффициент нагрузки, получим
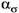 - теоретический коэффициент концентрации напряжений в корне зуба.
- теоретический коэффициент концентрации напряжений в корне зуба.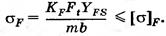 где
где  - коэффициент формы зуба.
- коэффициент формы зуба.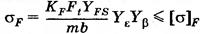
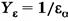 - коэффициент, учитывающий торцевое перекрытие.
- коэффициент, учитывающий торцевое перекрытие.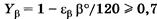 - коэффициент, учитывающий наклон зуба, получен экспериментально.
- коэффициент, учитывающий наклон зуба, получен экспериментально. 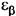 - коэффициент осевого перекрытия.
- коэффициент осевого перекрытия.


