
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определим частость и накопленную частость для каждого интервала по формуламСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где
7. Строим график плотности распределения значений параметра 8. В соответствии с рекомендациями Тогда 9.Заключение: В предложенном примере количество двигателей с мощностью менее 85 л. с. составляет 5 единиц.
Рис. 2.1 – Графики плотности (Рi) и функции (Fi) распределения случайной величины
Задача 7. Определить предельно-допустимое значение диагностического параметра и характеристики случайной величины по статистической выборке 60 значений мощности, развиваемой двигателями транспортного средства, приведенной ниже (двухмодальное распределение параметра).
Таблица 2.4 - Значение мощности, развиваемой двигателями транспортного средства, л. с. Решение: Характеристиками случайной величины являются среднее значение случайной величины Определим эти характеристики
Примем
Случайные величины, у которых при 0,1< Точечные оценки позволяют предварительно судить о качестве изделий и технологических процессов. Чем ниже средний ресурс – Таким образом, мы определили характеристики случайной величины. Далее решение задачи осуществляем, аналогично решению задачи 6, выполняя действия, изложенные в п. 1…6. В результате выполнения этих действий мы получим распределение параметра по интервалам (табл. 2.5).
Таблица 2.5 - Распределение параметра по интервалам
По полученным значениям частостей (см. табл. 3) построим кривую плотности распределения (рис. 2). Как видно из рис. 2, мы имеем двухмодальное распределение. Для решения задачи необходимо из выборки значений случайной величины отбросить те значения, которые создают левый “пик” на графике. Из графика (рис. 2.2) видно, что необходимо убрать значения, лежащие в интервале 51 – 75 л. с. Это такие значения: 51, 55, 58, 61, 64, 65, 65, 57, 58 – всего их 9. По оставшейся выборке составляем новое распределение параметра по интервалам (табл. 2.6) и строим графики плотности и функции распределения параметра (рис. 2.3).
Таблица 2.6 - Распределение параметра по интервалам
Для
Рис. 2.2 – График плотности распределения случайной величины
Рис. 2.3 – Графики плотности (Рi) и функции распределения (Fi) случайной величины
Задача 1 Условие. В течение некоторого периода времени проводилось наблюдение за работой одного восстанавливаемого изделия. За весь период наблюдения было зарегистрировано n отказов. До начала наблюдения изделие проработало t1 час, к концу наблюдения наработка изделия составила t2 час. Требуется определить среднюю наработку на отказ
Таблица 3.1
Задача 2. В течение некоторого времени проводилось наблюдение за работой N 0 экземпляров восстанавливаемых изделий. Каждый из образцов проработал t i часов и имел п i отказов. Требуется определить среднюю наработку на отказ по данным наблюдения за работой всех изделий. Исходные данные для расчёта приведены в табл. 3.2. Таблица 3.2
Задача 3. Система состоит из N приборов, имеющих разную надёжность. Известно, что каждый из приборов, проработав вне системы t i часов, имел п i отказов. Для каждого из приборов справедлив экспоненциальный закон распределения отказов. Найти среднюю наработку на отказ всей системы. Исходные данные для расчёта в табл. 3.3. Таблица 3.3
Задача 4. Система состоит из k групп элементов. В процессе эксплуатации зафиксировано п отказов. Количество отказов в j –й группе равно n j; среднее время восстановления элементов j –й группы равно t j. Требуется вычислить среднее время восстановления системы. Исходные данные для расчёта приведены в табл. 3.4. Таблица 3.4
Задача 5. Изделие имеет среднюю наработку на отказ t ср и среднее время восстановления t в. Требуется определить коэффициент готовности изделия. Исходные данные для расчёта приведены в табл. 3.5. Таблица 3.5
Задача 6. Определить предельно-допустимое значение диагностического параметра по статистической выборке n значений мощности, развиваемой двигателями транспортного средства, приведенной ниже. Вариант 1 (к задаче 6) (выборка из 30 значений, л. с.)
Вариант 2 (к задаче 6) (выборка из 40 значений, л. с.)
Вариант 3 (к задаче 6) (выборка из 50 значений, л. с.)
Вариант 4 (к задаче 6) (выборка из 30 значений, кВт.)
Вариант 5 (к задаче 6) (выборка из 40 значений, кВт.)
Вариант 6 (к задаче 6) (выборка из 50 значений, кВт.)
Вариант 7 (к задаче 6) (выборка из 30 значений, л. с.) Вариант 8 (к задаче 6) (выборка из 40 значений, л. с.)
Вариант 9 (к задаче 6) (выборка из 50 значений, л. с.) Вариант 10 (к задаче 6) (выборка из 30 значений, кВт.) Вариант 11 (к задаче 6) (выборка из 40 значений, кВт.) Вариант 12 (к задаче 6) (выборка из 50 значений, кВт.) Вариант 13 (к задаче 6) (выборка из 30 значений, л. с.) Вариант 14 (к задаче 6) (выборка из 40 значений, л. с.) Вариант 15 (к задаче 6) (выборка из 50 значений, л. с.) Вариант 16 (к задаче 6) (выборка из 30 значений, кВт.) Вариант 17 (к задаче 6) (выборка из 40 значений, кВт.) Вариант 18 (к задаче 6) (выборка из 50 значений, кВт.) Вариант 19 (к задаче 6) (выборка из 30 значений, л. с.) Вариант 20 (к задаче 6) (выборка из 40 значений, л. с.) Вариант 21 (к задаче 6) (выборка из 50 значений, л. с.) Вариант 22 (к задаче 6) (выборка из 30 значений, кВт.) Вариант 23 (к задаче 6) (выборка из 40 значений, кВт.)
|

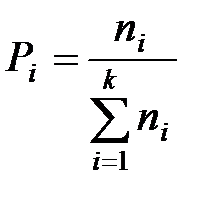 ,
,  ,
,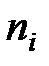 - количество значений параметра;
- количество значений параметра; - общее количество значений мощности по статистической выборке.
- общее количество значений мощности по статистической выборке. и кривую функции распределения
и кривую функции распределения 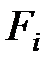 (см. рис.1).
(см. рис.1). принимаем, что состояние автомобильного парка должно соответствовать обеспечению
принимаем, что состояние автомобильного парка должно соответствовать обеспечению  - ресурсного пробега. Для двигателей
- ресурсного пробега. Для двигателей  .
. , т. е. общее число автомобилей, имеющих мощность двигателя ниже предельно-допустимого значения должно быть не более 15 %. Откладываем на оси ординат значение 0,15 и проводим горизонталь до пересечения с кривой функции распределения
, т. е. общее число автомобилей, имеющих мощность двигателя ниже предельно-допустимого значения должно быть не более 15 %. Откладываем на оси ординат значение 0,15 и проводим горизонталь до пересечения с кривой функции распределения  i. На оси абсцисс находим значение параметра, соответствующее точке пересечения горизонталей с кривой
i. На оси абсцисс находим значение параметра, соответствующее точке пересечения горизонталей с кривой 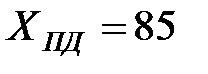 л. с.
л. с. , ее среднеквадратическое отклонение
, ее среднеквадратическое отклонение  и вариация, которая оценивается коэффициентом вариации
и вариация, которая оценивается коэффициентом вариации  .
. л. с.
л. с. л. с. (для упрощения расчетов)
л. с. (для упрощения расчетов) л. с.
л. с. .
. , имеют малую вариацию;
, имеют малую вариацию;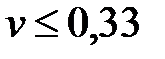 - среднюю вариацию; при
- среднюю вариацию; при 



 произведем действия по определению предельнодопустимого значения диагностического параметра. Получим
произведем действия по определению предельнодопустимого значения диагностического параметра. Получим  л. с.
л. с.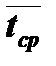 . Исходные данные в табл. 3.1.
. Исходные данные в табл. 3.1. , час
, час

 , час
, час

 , час
, час

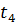 , час
, час

 , час
, час

 мин.
мин.
 мин.
мин.
 мин.
мин.
 мин.
мин.
 мин.
мин.
 , час.
, час.
 , час.
, час.



