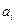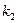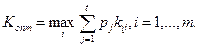Матрица эффективности программных продуктов

	0,1	0,5	0,1	0,2
	0,2	0,3	0,2	0,4
	0,1	0,4	0,4	0,3

Критерий среднего выигрыша. Данный критерий предполагает задание вероятностей состояний обстановки р_i.. Эффективность систем оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по всем состояниям обстановки:

Оптимальной системе будет соответствовать эффективность

Если в данном примере задаться вероятностями применения противником программных воздействий p ₁ = 0,4, р ₂ = 0,2, р ₃ = 0,1 и p₄ = 0,3, то получим следующие оценки систем:

К (а ₁)= 0,4 0,1+0,2 0,5+0,1 0,1+0,3 0,2=0,21;

К (а ₂) = 0,4 0,2 + 0,2 0,3 + 0,1 • 0,2 + 0,3 0,4 = 0,28;

К (а ₃) = 0,4×0,1+0,2 0,4+0,1×0,4+0,3×0,3 = 0,25.

Оптимальное решение — система а₂.

Для применения критерия среднего выигрыша необходим, по существу, перевод операции из неопределенной в вероятностную, причем произвольным образом.

Критерий Лапласа. В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными. Исходя из этого

Рассчитаем эффективность систем по данному критерию для приведенного примера:

К (а ₁) = 0,25 (0,1 + 0,5 + 0,1 + 0,2) = 0,225;

К (а ₂) = 0,25 (0,2 + 0,3 + 0,2 + 0,4) = 0,275;

К (а ₃) = 0,25 (0,1 + 0,4 + 0,4 + 0,3) = 0,3.

Оптимальное решение — система а₃. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

Критерий осторожного наблюдателя (Вальда). Это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях. Критерий основывается на том, что, если состояние обстановки неизвестно, нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы.

В каждой строке матрицы эффективности находится минимальная из оценок систем по различным состояниям обстановки

Оптимальной считается система из строки с максимальным значением эффективности:

Применение критерия максимина к нашему примеру дает следующие оценки:

К (а ₁) = min(0,1; 0,5; 0,1; 0,2) = 0,1;

К (а ₂) = min(0,2; 0,3; 0,2; 0,4) = 0,2;

К (а ₃) = min(0,1; 0,4; 0,4; 0,3) = 0,1.

Оптимальное решение — система а₂.

Максиминный критерий ориентирует на решение, не содержащее элементов риска: при любом из возможных состояний обстановки выбранная система покажет результат операции не хуже найденного максимина. Такая осторожность является в ряде случаев недостатком критерия. Другой недостаток — он не удовлетворяет требованию 3 (добавление постоянного числа к каждому элементу столбца матрицы эффективности влияет на выбор системы).

 

Критерий максимакса. Этим критерием предписывается оценивать системы по максимальному значению эффективности и выбирать в качестве оптимального решения систему, обладающую эффективностью с наибольшим из максимумов:

Оценки систем на основе максимаксного критерия в нашем примере принимают такие значения:

К (а ₁) = max (0,1; 0,5; 0,1; 0,2) = 0,5;

К (а ₂) = max (0,2; 0,3; 0,2; 0,4) = 0,4;

К (а ₃) = max (0,1; 0,4; 0,4; 0,3) = 0,4,

Оптимальное решение — система а₁. Критерий максимакса самый оптимистический критерий. Те, кто предпочитает им пользоваться, всегда надеются на лучшее состояние обстановки и, естественно, в большой степени рискуют.

Критерий пессимизма-оптимизма (Гурвица). Это критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем неразумно проявлять как осторожность, так и азарт, а следует, учитывая самое высокое и самое низкое значения эффективности, занимать промежуточную позицию (взвешиваются наихудшие и наилучшие условия), Для этого вводится коэффициент оптимизма a (0 < a < 1), характеризующий отношение к риску лица, принимающего решение. Эффективность систем находится как взвешенная с помощью коэффициента aсумма максимальной и минимальной оценок:

Условие оптимальности записывается в виде

Зададимся значением a = 0,6 и рассчитаем эффективность систем для рассматриваемого примера:

К (а ₁) = 0,6×0,5+(1-0,6)×0,1 = 0,34;

К (а ₂) = 0,6×0 5+(1-0,6)×0,2 = 0,32;

К (а ₃) = 0,6×0,4+(1-0,6)×0,1 = 0,34.

Оптимальной системой будет а₁.

При a =0 критерий Гурвица сводится к критерию максимина, при a =1 — к критерию максимакса. Значение aможет определяться методом экспертных оценок. Очевидно, что, чем опаснее оцениваемая ситуация, тем ближе величина a должна быть к единице, когда гарантируется наибольший из минимальных выигрышей или наименьший из максимальных рисков.

На практике пользуются значениями коэффициента aв пределах 0,3 — 0,7. В критерии Гурвица не выполняются требования 4 и 5.

Критерий минимального риска (Сэвиджа). Минимизирует потери эффективности при наихудших условиях. Для оценки систем на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце:

После преобразования матрицы используется критерий минимакса:

Оценим эффективность систем из приведенного примера в соответствии с данным критерием. Матрице эффективности (см. табл. 2.11) будет соответствовать матрица потерь (табл. 2.12).

Таблица 2.12

Матрица потерь

	0,1		0,3	0,2
			0,2
	0,1	0,1		0,1

 

Тогда

К (а ₁) =max(0,1; 0; 0,3; 0,2) =0,3;

К (а ₂) = mах(0; 0,2; 0,2; 0) = 0,2;

К (а ₃) = mах(0,1; 0,1; 0; 0,1) = 0,1.

Оптимальное решение— система а₁. Критерий минимального риска отражает сожаление по поводу того, что выбранная система не оказалась наилучшей при определенном состоянии обстановки. Так, если произвести выбор системы а₁, а состояние обстановки в действительности n₃, то сожаление, что не выбрана наилучшая из систем (а₃), составит 0,3. О критерии Сэвиджа можно сказать, что он, как и критерий Вальда, относится к числу осторожных критериев. По сравнению с Критерием Вальда в нем придается несколько большее значение выигрышу, чем проигрышу. Основной недостаток критерия — не выполняется требование 4.

Таким образом, эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

ü природа конкретной операции и ее цель (в одних операциях допустим риск, в других — нужен гарантированный результат);

ü причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

ü характер лица, принимающего решение (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Выбор какого-то одного критерия приводит к принятию решения по оценке систем, которое может быть совершенно отличным от решений, диктуемых другими критериями. Это наглядно подтверждают результаты оценки эффективности систем применительно к примеру 2.2 по рассмотренным критериям (табл. 2.13).

 

Таблица 2.13