Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идеальная оптическая системаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Идеальная оптическая система изображает точку в виде точки, т.е. все лучи, исходящие из любой точки предмета, собираются после выхода из системы в одной точке изображения. Другими словами под идеальной оптической системой понимают такую оптическую систему, которая не нарушает гомоцентричности прошедших через нее лучей. Теория идеальной оптической системы разработана Гауссом и имеет чисто геометрический характер. Реальные оптические системы, состоящие из сферических и плоских преломляющих и отражающих поверхностей, в общем случае не удовлетворяют положениям теории идеальных оптических систем. Изображением светящейся точки на экране в реальной оптической системе будет не точка, а светлое пятно. Реальные оптические системы ведут себя как идеальные лишь для лучей, распространяющейся вдоль оси центрированной оптической системы, когда лучи образуют очень малые углы с оптической осью и нормалями к преломляющим и отражающим поверхностям системы. В этом случае (если e ‹‹ 1рад) и, пользуясь разложением в ряд Тейлора функций sin e:
можно положить sin e - e, где e выражается в радианах.
Область, в пределах которой можно делать такие замены, называется параксиальной, а соответствующие пучки лучей называют параксиальными (или нулевыми). В этой области закон преломления света можно записать в следующем виде:
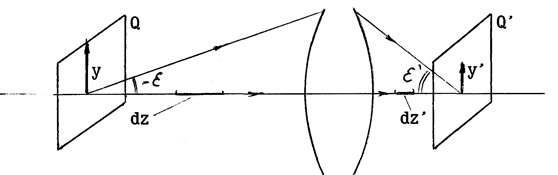
Линейное, угловое и продольное увеличение оптической системы Выберем в предметной плоскости Q перпендикулярной оптической оси отрезок длиной y. Его изображение будет расположено в сопряженной плоскости Q ¢ и будет иметь линейные размерыy¢ (рис.4). Отношение размера изображения к размеру предмета называют линейным увеличением оптической системы (b): b = У ¢ / У. (3) Для пары сопряженных плоскостей Q и Q ' перпендикулярных оптической оси линейное увеличение постоянно и не зависит от величины предмета. При b › 0 изображение перевернутое, при b ‹ 0 - изображение прямое.
Рис.4. К определению увеличения оптической системы. Угловым увеличением оптической системы (¡) называют отношение тангенсов углов образованных сопряженными лучами с оптической осью: ¡ = tg e ¢ / tg e. (4) Продольным увеличением оптической системы (a) называют отношение размера изображения бесконечно малого отрезка, расположенного вдоль оптической оси, к размеру этого отрезка:
a = dz ¢ / dz. (5) Кардинальные элементы оптической системы Идеальная оптическая система обладает рядом кардинальных элементов - передний и задний фокусы, передние и задние главные и узловые точки, передние и задние фокальные и главные плоскости, переднее и заднее фокусные расстояния. Знание четырех кардинальных точек (обычно это фокусы и главные точки) полностью определяет работу оптической системы, т.е. мы можем построить изображение любой точки, пользуясь только кардинальными элементами и совершенно не рассматривая действительного хода лучей в данной оптической системе.
2.5.1. Задний фокус и задняя фокальная плоскость оптической системы. Задним фокусом оптической системы называют изображение бесконечно удаленной точки, расположенной на оптической оси. Лучи, выходящие из бесконечно удаленной точки на оптической оси, падают на оптическую систему параллельно оптической оси. Поэтому можно сказать, что задним фокусом оптической системы называется точка (F '), в которой собирается пучок лучей, падающих на систему параллельно ее оптической оси (рис.5).
Рис.5. Задний фокус и задняя фокальная плоскость оптической системы. Плоскость (Qf), проходящая через задний фокус и перпендикулярная оптической оси, называется задней фокальной плоскостью оптической системы. Эта плоскость является изображением бесконечно удаленной плоскости. Параллельный пучок лучей, падающий на оптическую систему под углом к оптической оси (e), идет из бесконечно удаленной точки, расположенной вне оптической оси, и после выхода из оптической системы собирается в сопряженной точке С', которая находится вне оптической оси, в задней фокальной плоскости.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.144 (0.011 с.) |

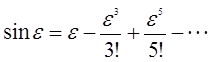 (1)
(1)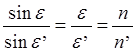 (2)
(2)