Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерферометрический синтез изображенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис 9.10 В предыдущем разделе мы заявили, что альтернативой проекту TPF может стать интерферометр. Например, это может быть многоапертурный интерферометр, способный давать (размытые) изображения экзопланет, даже таких небольших как Земля. Европейское космическое агентство (ESA) планирует вывести на орбиту интерферометр "Дарвин" (Darwin). По одному из его конкретных проектов (рис. 9.10) он будет состоять из шести телескопов с диаметром зеркала у каждого в несколько метров. Телескопы будут размещены по окружности диаметром около 100 м и смогут изменять взаимное положение, двигаясь по кругу и смещаясь по радиусу. Собранный ими свет будет направляться в центральный аппарат, где и произойдёт синтез изображения. "Дарвин" будет наблюдать в среднем инфракрасном диапазоне, вблизи 10 мкм. Выбор диапазона обусловлен следующими причинами: во-первых, в этих лучах не так велика разница в яркости звезды и планеты (разд. 9.1), а во-вторых, именно в этом диапазоне заключена ценная информация о возможности жизни на экзопланетах (гл. 12). Разумеется, выбор диапазона продиктован и общим интересом к инфракрасному изображению космоса, поскольку возможности наземной интерферометрии в среднем ИК-диапазоне весьма ограничены из-за сильного поглощения в атмосфере Земли и её собственного излучения в этом диапазоне (разд. 9.3). Размещение инфракрасного интерферометра в космосе дает массу преимуществ, порой весьма неожиданных. Например, там легче и точнее можно менять положение телескопов по сравнению с поверхностью Земли, которая, к тому же, постоянно вибрирует. А для проведения измерений необходимо либо поддерживать конфигурацию интерферометра с точностью до малых долей длины волны наблюдаемого излучения (т. е. существенно лучше, чем 10 мкм), либо с такой же точностью измерять положение каждого телескопа, а затем при помощи оптических линий задержки исправлять ошибки положения. Для этого "Дарвин" будет снабжен системой лазерного контроля за положением телескопов, а также реактивными двигателями коррекции на каждом из них.
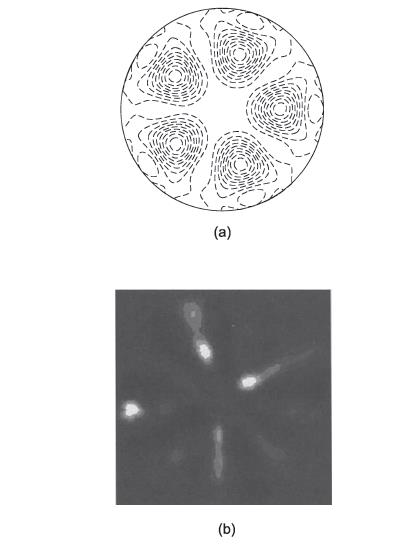
Рис 9.11 "Дарвин" будет использовать принцип нуль-интерферометрии: оптические пути от каждого телескопа до центрального аппарата будут подобраны так, чтобы волны от объекта, лежащего на оптической оси системы, складываясь в изображении, взаимно гасили, "обнуляли" друг друга. Пример этого для системы из пяти телескопов показан на рис. 9.11(а). Пять контурных "холмов" указывают зоны наименьшего ослабления в этой конфигурации. Яркость звезды, расположенной на оптической оси, будет сильно подавлена (но не полностью, из-за конечного размера её изображения). Получив множество интерференционных картин при различных радиальных и угловых положениях телескопов, можно синтезировать двумерное изображение планетной системы с «обнулённым» изображением центральной звезды. Рис. 9.11(б) показывает, как бы в этом случае выглядела наша Солнечная система. Три ярких пятна – это Венера, Земля и Марс, а остальные детали – это ложные изображения, возникшие из-за неполного заполнения общей апертуры телескопами в их различных положениях. Возможно, уже в середине следующего десятилетия "Дарвин" и TPF (который будет наблюдать в видимом диапазоне) окажутся на орбите; ну по крайней мере – один из них. Тогда мы сможем открывать землеподобные планеты в десятках световых лет от нас. Чтобы обнаружить такую планету, любому из этих телескопов понадобится всего несколько часов накопления света, и всего несколько недель наблюдений, чтобы обнаружить на ней признаки жизни (гл. 12). Кроме этого, сейчас разрабатываются методы нуль-интерферометрии для наземных телескопов, например, для VLT и "Кек". Они подготовят почву для "Дарвина" и TPF, хотя и не смогут сравниться с ними в эффективности. Так или иначе, в настоящее время прямое обнаружение экзопланет из космоса или с поверхности Земли весьма проблематично. Поэтому не следует забывать о возможностях косвенных методов обнаружения и исследования экзопланет. Этому посвящена следующая глава.
Резюме
* Прямое обнаружение экзопланет затруднено тем, что они располагаются очень близко к гораздо более ярким объектам – их звёздам. * Коронограф облегчает обнаружение планеты, уменьшая интенсивность функции рассеяния точки (ФРТ) звезды значительно сильнее, чем планеты. * Атмосфера Земли поглощает излучение в некоторых диапазонах длин волн, особенно – в инфракрасном и ультрафиолетовом. К тому же, она сама излучает в среднем инфракрасном диапазоне и частично рассеивает излучение всех длин волн. Всё это снижает отношение сигнала к шуму в изображении и тем самым осложняют задачу обнаружения планеты. * Кроме того, атмосферная турбулентность ухудшает качество изображений, создавая видимость уширения ФРТ телескопа. Это уширение можно частично скомпенсировать методом адаптивной оптики в небольшом поле зрения вокруг опорной «звезды». * Пока возможности прямого обнаружения экзопланет даже крупнейшими наземными телескопами (например, VLT или "Кек") весьма ограничены, но можно надеяться, что к 2010 году VLT будет способен регистрировать планеты типа Юпитера на расстоянии до 15 св. лет. Еще лучшими возможностями будет обладать космический телескоп "Джеймс Вебб", запланированный к запуску в 2010 году. Телескоп ELT (с диаметром зеркала около 30 м), оснащенный адаптивной оптикой, позволит регистрировать планеты типа Юпитера на расстояниях в сотни световых лет, а планеты типа Земли – на расстояниях в десятки световых лет. Его постройка запланирована на 2014 г. * Космический интерферометр "Дарвин" и обсерватория TPF будут способны не только получать изображения экзопланет тип Земли на расстояниях в десятки световых лет, но и искать на них следы биосферы. Реальные сроки их запуска – в районе 2015 года. * Несмотря на постоянное совершенствование аппаратуры, прямое обнаружение экзопланет (как из космоса, так и с Земли) в настоящее время представляется маловероятным.
Вопросы
Ответы даны в конце книги.
Вопрос 9.1. (а) Опишите качественно, как изменится контраст изображения Земли (рис. 9.1), если она приблизится к Солнцу. (б) Рассмотрите причины, по которым прямое обнаружение Земли станет (i) легче или (ii) сложнее, если она приблизится к Солнцу.
Вопрос 9.2. Объясните, почему в космических телескопах следует использовать коронограф, а не адаптивную оптику.
Вопрос 9.3. Объясните, какую роль играет: (i) размер объектива одиночного телескопа; (ii) расстояние между телескопами в интерферометре.
Подписи к рисункам Рис. 9.1. Спектры Солнца, Юпитера, Земли и Урана в одинаковом масштабе. Заметьте, что указана энергия, излучаемая в единичном интервале частоты, а не длины волны, поэтому положения пиков интенсивности немного смещены. Рис. 9.2. (а) Телескоп-рефлектор с оптически совершенным круглым зеркалом диаметром D создает изображение удаленного точечного объекта; (б) Так выглядит изображение далёкого точечного объекта и соответствующая ему ФРТ (функция рассеяния точки) зеркала телескопа. Рис. 9.3. Сечение изображений звезды и планеты, разделённых углом q p. Изображения построены оптически идеальным круглым зеркалом диаметром D. Рис. 9.4. Дифракционно-ограниченная ФРТ и ФРТ коронографа Лио. q – угловое расстояние от центра фокальной плоскости, измеренное в единицах l/ D, где D – диаметр зеркала, а l – длина волны света.
Рис. 9.5. Спектр поглощения земной атмосферы на уровне моря в безоблачную погоду для источника, наблюдаемого высоко над горизонтом. Интенсивность полос, связанных с Н2О, меняется в зависимости от влажности воздуха. Рис. 9.6. (а) Типичная система адаптивной оптики; (б) Изображение участка звездного неба до и после обработки методами адаптивной оптики. Isaac Newton Group of Telescopes/Astronomy Technology Centre. Durham University. Рис. 9.7. Возможно, так будет выглядеть гигантский телескоп OWL Европейской южной обсерватории European Southern Observatory.
Рис. 9.8. (а) Электромагнитная волна. (б) Волны усиливают друг друга. (в) Волны одинаковой амплитуды нейтрализуют друг друга. Рис. 9.9. (а) Изображение звезды в простом двухзеркальном интерферометре. (б) Построенное тем же интерферометром изображение звезды с планетой (по сравнению с верхним рисунком горизонтальный масштаб растянут).
Рис. 9.10. Проект космического интерферометра "Дарвин" Европейского космического агентства. Вариант с шестью зеркалами при диаметре каждого из них около 1,5 м. Alcatel/ESA. Рис. 9.11. (а) Карта ослабления в плоскости изображения нуль-интерферометра из пяти телескопов. Пять контурных "холмов" указывают зоны наименьшего ослабления. (б) Так интерферометр "Дарвин" мог бы увидеть Солнечную систему; три ярких пятна – Венера, Земля и Марс. (b) Mennesson and Mariotty. Надписи на рисунках Рис. 9.1. 1 – Длина волны, мкм 2 – Поток энергии (условные единицы) 3 – ультрафиолет 4 – видимый свет 5 – инфракрасное излучение 6 – Солнце 7 – Юпитер 8 – Земля 9 – Уран
Рис. 9.2. 1 – Плоские волновые фронты от удаленного точечного объекта 2 – Фокальная плоскость 3 – Зеркало диаметром D 4 – Изображение (негатив) 5 – Яркость (условные единицы)
Рис. 9.3. 1 – Фокальная плоскость 2 – Звезда 3 – Планета 4 – Зеркало диаметром D 5 – Яркость (условные единицы) Рис. 9.4. 1 – Яркость (условные единицы) 2 – Круглая апертура 3 – Коронограф Лио 4 – Планета
Рис. 9.5. 1 – Поглощение, % 2 – Длина волны, мкм 3 – Видимый диапазон
Рис. 9.6. 1 – Волновой фронт за пределом земной атмосферы 2 – Волновой фронт, искаженный земной атмосферой 3 – Качающееся зеркало 4 – Деформируемое зеркало 5 – Камера 6 – Датчик волнового фронта 7 – До 8 – После Рис. 9.8. 1 – Электрическое поле 2 – Магнитное поле 3 – Направление распространения 4 – В фазе 5 – В противофазе
Рис. 9.9. 1 – Плоскость изображения 2 – Изображение звезды 3 – Яркость изображения 4 - проп. 1/ D 5 - проп. 1/ d 6 – Звезда 7 – Планета
Барри Джонс. Жизнь в Солнечной системе и за её пределом. Шпрингер, 2004.
Глава 10. Поиск планет: косвенные методы
Хотя прямыми методами мы сможем изучить экзопланету намного полнее, чем косвенными, маловероятно, что в ближайшие годы у нас будем возможность непосредственно наблюдать движение планет вокруг других звезд. Поэтому сейчас мы можем полагаться лишь на менее информативные косвенные методы, которые позволяют нам судить о наличии планеты по её воздействию на движение звезды, вокруг которой она обращается, или по вызванному ей изменению яркости самой звезды или объектов фона.
10.1. Обнаружение планеты по движению её звезды
10.1.1. Влияние планеты на движение её звезды
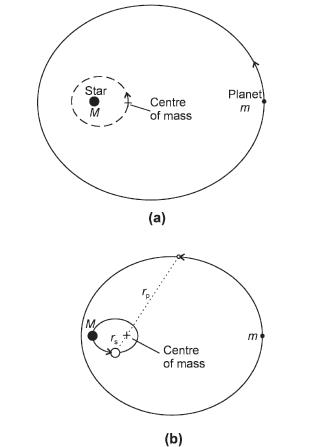
Рис 10.1 Рисунок 10.1(а) показывает, как обычно изображают движение планеты относительно центральной звезды; на нем планета обращается вокруг неподвижной звезды. Однако движение этих тел можно изобразить и в другой системе координат, связанной с их общим центром масс, вокруг которого обращаются по своим орбитам как планета, так и звезда (рис. 10.1(б)). Положение центра масс при этом определяется уравнением
M ´ r s = m ´ r p (10.1),
где M и m – это массы звезды и планеты соответственно, а r s и r p – их текущие расстояния от центра масс. Это уравнение справедливо для всех точек орбиты, включая значения r s и r p, соответствующие положениям на больших полуосях орбит (a s и a p) по отношению к центру масс. Следовательно
M ´ a s = m ´ a p (10.2)
Экцентриситеты e и периоды P для всех трёх орбит, показанных на рис. 10.1, одинаковы. Как известно, планета движется вокруг звезды (рис. 10.1(а)) с неравномерной скоростью: в соответствии со вторым законом Кеплера (разд. 1.1.1) максимальная скорость достигается в периастре (ближайшая к звезде точка орбиты), а минимальная – в апоастре (наиболее удаленная от звезды точка). Эти же закономерности сохраняются и при движении звезды и планеты вокруг их общего центра масс (рис. 10.1(б)), так что максимальные скорости достигаются в перицентрах (ближайшие к центру масс точки орбит), а минимальные – в апоцентрах. Заметим, что a = a s + a p. А поскольку для звезд и планет M» m, а значит, a p» a s, можно считать, что a» a p. Таким образом, любая звезда, вокруг которой обращается планета, сама движется по небольшой орбите. Это периодическое движение накладывается на стационарное перемещение звезды в пространстве, называемое её собственным движением. Если мы сможем зарегистрировать орбитальный компонент в движении звезды, то тем самым мы обнаружим присутствие планеты и сможем кое-что узнать об её массе и орбите. Для измерения орбитального движения звезды применяются методы астрометрии и доплеровской спектроскопии.
10.1.2. Принципы астрометрии Астрометрия занимается высокоточным измерением положений звезд на небесной сфере в последовательные моменты времени. Анализируя затем траекторию звезды, можно попытаться выявить в ней орбитальный компонент. Возможность его выявления зависит от углового размера (b) орбиты звезды. Для определения b мы перепишем уравнение (10.2) в виде a s = (m / M) a p. Обозначив расстояние от нас до звезды через d и использовав полученное выше приближение (a» a p), имеем:
где угол b измеряется в радианах. Это уравнение справедливо в том случае, когда большая полуось орбиты звезды лежит в плоскости небесной сферы, иначе измеренный нами размах смещения звезды будет меньше, чем a s. Мы можем выразить b через орбитальный период системы (P), использовав связь между a и P, вытекающую из Ньютоновых законов движения и тяготения:
Из уравнений (10.3) и (10.4) следует, что
(Заметим, что из уравнения (10.4) для Солнечной системы вытекает Третий закон Кеплера, описанный в разд. 1.1.1.) Из уравнения (10.3) следует, что астрометрический сигнал b возрастает • с увеличением отношения m / M; • с увеличением значения a (и, соответственно, с ростом P); • с уменьшением значения d. Как и следовало ожидать, легче всего обнаружить массивную планету, обращающуюся по большой орбите вокруг маломассивой звезды, если наблюдать её с небольшого расстояния. Но движение по большой орбите происходит с большим периодом, поэтому накопление измерений на значительном участке орбитальной траектории потребует многих лет наблюдений.
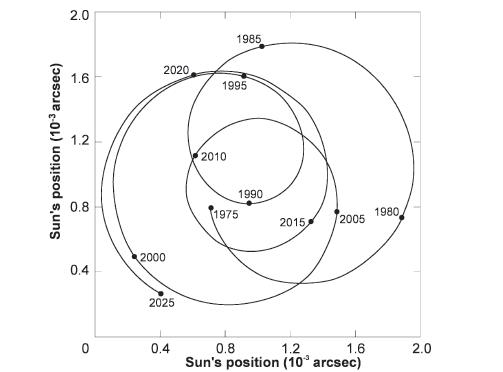
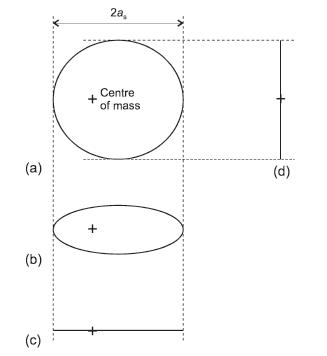
Рис 10.2 На рис. 10.2 приведены значения величины b ´ d для некоторых конкретных случаев. Чтобы лучше понять смысл представленных на рисунке зависимостей, вообразим себе Солнечную систему, в которой присутствует лишь одна планета (например, Юпитер). Тогда Солнце будет двигаться по орбите с большой полуосью a s = 7,4 ´ 108 м, что ненамного превышает радиус самого Солнца (6,96 ´ 108 м). Период обращения Юпитера равен 4,33 ´ 103 суток, так что отсчёт по соответствующей линии на рис. 10.2 дает значение b ´ d = 1,6 ´ 10–2 угл. сек ´ св. лет. Для расстояния в 30 св. лет мы получим отсюда угол b = 5,3 ´ 10–4 ², или 530 микросекунд дуги. Под таким крошечным углом видна, например, толщина человеческому пальца с расстояния 7000 км! Так что для астрометрии задача обнаружения планет является весьма сложной. В рассмотренном примере предполагалось, что большая полуось a s орбиты звезды лежит в плоскости небесной сферы. Если это не так, то ситуация еще хуже, поскольку тогда мы видим в проекции отрезок короче a s. Посмотрим на рис.10.3. Если орбита развернута к нам плашмя (рис. 10.3(а)) или как-то иначе, но так что большая полуось a s располагается в плоскости небесной сферы (рис.10.3(б) и 10.3(в)), то мы наблюдаем полный размах смещений звезды, равный 2 a s. Но если орбита ориентирована по-другому, мы увидим смещение меньшее полного размаха. Самый неудачный случай показан на рис.10.3(г), где большая полуось направлена перпендикулярно плоскости неба, вследствие чего мы можем наблюдать только минимальное смещение звезды, равное двум малым полуосям эллиптической орбиты.
Рис 10.3 Возникает вопрос, а можно ли определить истинную орбиту, если она не развернута к нам плашмя? Оказывается – можно. Посмотрим на рис. 10.3(б). Если бы наблюдаемая орбита была истинной, то она должна была бы иметь гораздо больший эксцентриситет, чем истинная орбита на рис. 10.3(а), а центр масс системы заметно сдвинулся бы влево. Более того, движение звезды по орбите в этом случае должно было бы иметь совершенно иной характер (например, разница орбитальных скоростей в перицентре и апоцентре должна была бы быть гораздо больше). Таким образом, измеряя достаточно точно интервалы времени между различными точками видимой орбиты звезды, можно найти истинную орбиту при любой ориентации ее плоскости. А значит, можно определить значение величины b, входящей в уравнения (10.3) и (10.5), которое соответствует истинному значению a s.
Массы и орбиты планет
Чтобы определить массу планеты, преобразуем уравнение (10.5) к виду
где параметры b и P регистрируются при наблюдении за движением звезды, а расстояние d определяется какими-либо другими астрономическим методами, например, тригонометрическими измерениями параллакса звезды (см. раздел 1.3.1). В уравнение входит также масса звезды М, которую мы можем определить следующим образом. Оптический спектр подтвердит, что это звезда главной последовательности, из числа тех, которые нас интересуют. Поэтому, измерив ее светимость и воспользовавшись соотношением «масса – светимость» (рис. 8.1), мы можем вычислить массу звезды. Заметим, что само соотношение «масса – светимость» было получено на основе анализа движения звезд относительно друг друга в двойных системах, о чем можно узнать из книг по астрономии (см. Приложение). Зная P и М, легко можно определить большую полуось a орбиты планеты из уравнения (10.4). Эксцентриситет орбиты планеты такой же, как у орбиты звезды (рис. 10.1), величина которого известна, поскольку, как сказано выше, по наблюдениям мы можем найти истинную орбиту звезды. На практике варьируют параметры орбиты, пока она не станет наилучшим образом удовлетворять результатам наблюдений. Естественно, астрономические измерения всегда содержат некоторую неточность, ведущую к соответствующим неточностям в значениях массы и параметрах орбиты предполагаемой планеты.
Рис 10.4 До сих пор мы рассматривали звезду с одной планетой. Наличие нескольких планет существенно усложняет характер орбиты звезды. Это демонстрирует рис. 10.4, где показано движение Солнца в плоскости земной орбиты орбиты при наблюдении с расстояния в 30 св. лет. Наибольшее воздействие на движение Солнца, естественно, оказывает Юпитер, однако наличие других планет (особенно Сатурна) приводит к тому, что траектория Солнца значительно отличается от простого эллипса. Конечно, проведя большое количество тщательных измерений, можно «распутать» сложную картину и выявить роль отдельных планет. В случае с Солнцем нетрудно было бы выделить воздействие Юпитера и Сатурна, определив при этом их орбиты и массы, но значительно сложнее было бы найти массы и орбиты остальных, более мелких планет.
10.1.3. Астрометрические измерения
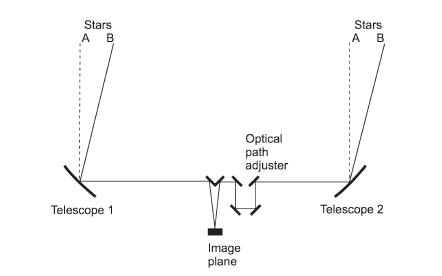
Основной проблемой астрометрии является выбор системы отсчёта, в которой следует измерять смещения изучаемой звезды. В качестве такой системы выбирают несколько других звезд, по отношению к которым и производят многократные измерения положения интересующей нас звезды. Изменение этого положения может быть вызвано различием в собственном движении звезд, орбитальным движением исследуемой звезды или различием параллаксах при измерениях с Земли в различные сезоны года. Поэтому данные наблюдений должны быть тщательно обработаны, чтобы выявить возможное орбитальное движение изучаемой звезды. Первую серьезную попытку астрометрического обнаружения планет предпринял голландский астрономом Питер ван де Камп, который в 1937 г. начал свои наблюдения в обсерватории Спрул (штат Пенсильвания). Он использовал телескоп-рефрактор с линзовым объективом диаметром D = 0,61 м. Из уравнения (9.1) следует, что для волны длиной l = 0,5 мкм угловой радиус центрального диска дифракционно-ограниченной ФРТ (1,22l/ D рад) в этом случае составляет 0,2² . Точность определения положения центра диска будет в несколько раз выше. Ван де Камп регистрировал положение нескольких изучаемых звезд на фотопластинках в течение нескольких десятилетий и пришел к убеждению, что ему удалось обнаружить наличие планет у некоторых звезд. В частности, речь шла о звезде Барнарда, которая расположена на расстоянии 5,94 св. года от Земли и является второй ближайшей космической соседкой нашего Солнца, после тройной системы, состоящей из Проксимы Кентавра и двух звезд (А и В) Альфы Кентравра. К сожалению, после капитального ремонта телескопа в 1949 г. ван де Кампу пришлось отказаться от анализа данных, содержащихся на ранее отснятых фотопластинках, а юстировка телескопа в 1957 г. внесла дополнительные проблемы. Коллеги ван де Кампа поставили под сомнение его заявление об открытии планет, отчасти из-за юстировок 1957 года, отчасти из-за недостаточной экспозиции фотопластинок и использования малого числа опорных звезд. Ван де Камп скончался в 1995 г., уверенный, что у звезды Барнарда есть, по крайней мере, одна планета. Этого не подтверждают другие исследователи, хотя и признают, что в движении звезды наблюдаются какие-то непонятные колебания. В настоящее время некоторые астрономы продолжают вести астрометрические измерения с Земли, используя, как и ван де Камп, обычные телескопы с одной апертурой, но заменив в последние годы фотопластинки на более современные электронные приемники света. Однако никто из них пока не открыл планету. Иной подход к астрометрическим измерениям основан на применении интерферометра (раздел 9.5), позволяющего увеличить точность определения положения объекта по схеме, показанной на рис. 10.5. Если в поле зрения находится одна звезда, то её свет, пойдя через две апертуры, попадает на плоскость изображения с некоторой разницей фаз, в результате чего на ней возникают чередующиеся светлые и темные полосы. В тех точках изображения, где волны, идущие по разным оптическим путям, приходят с одинаковой фазой, они усиливаются, создавая светлые полосы; а складываясь в противофазе, они ослабляются. Если в другом направлении видна вторая звезда, то в плоскости изображения ее светлые полосы лежат в других местах.
Рис 10.5 . Наблюдатель может совместить положение полос опорной и измеряемой звезд, варьируя длину плеч интерферометра, что позволяет определить угловое расстояние между звездами [Это объяснение, как и схема интерферометра (рис. 10.5), слишком упрощены. Желающим глубже разобраться в предмете, рекомендую книгу А.А. Токовинина "Звездные интерферометры", М.: Наука, 1988. – Прим. ред. ]. Вообще говоря, базисная линия между телескопами обычно не параллельна линии, соединяющей измеряемые звезды, поэтому необходимо либо иметь возможность поворачивать базис телескопов, либо использовать дополнительные телескопы с различной ориентацией баз. Путем многократных измерений можно точно определить параметры движения наблюдаемой звезды по отношению к нескольким опорным фоновым звездам.
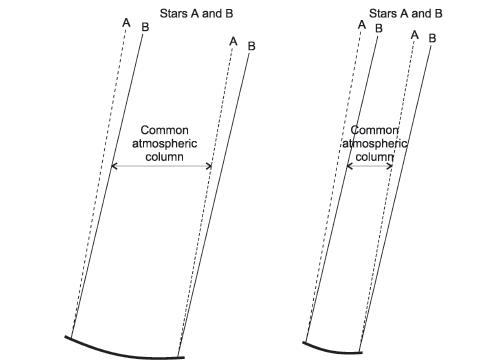
Рис 10.6 При помощи наземных астрометрических методов пока не удалось зафиксировать те малые движения звезд, которые возникают под влиянием планет. Причиной этому два фактора, связанные с атмосферой Земли. Во-первых, атмосферная рефракция зависит от угловой высоты объекта над горизонтом, поэтому в изображении возникают поперечные искажения, меняющиеся в зависимости от высоты центра изображения. Во-вторых, из-за упомянутой выше атмосферной турбулентности (раздел 9.3.1) изображение звезды дрожит, вследствие чего, даже в высокогорных обсерваториях, где влияние атмосферы слабее, точность измерений относительного расстояния между звездами обычно не превосходит 0,1². Степень дрожания изображения уменьшается при увеличении апертуры телескопа. Рассмотрим две звезды, разделенные малым угловым расстоянием (рис. 10.6). При большой апертуре свет каждой из звезд проходит практически через один и тот же атмосферный столб, поэтому относительные дрожания изображений звезд меньше, чем в телескопах с малой апертурой, где оптические пути света каждой из звезд различаются сильнее. Это различие возрастает с увеличением углового расстояния между звездами. Участок на плоскости изображения, где эффекты дрожания изображений почти совпадают, называется областью изопланатизма; его размер у 10-метрового телескопа на высокогорной обсерватории составляет в поперечнике около 50–100². В области этого пятна расстояние между изображениями двух звезд может быть измерено с точностью 10–4 ² или даже выше, если эти звезды не слишком слабые. При этом время накопления сигнала (чтобы собрать достаточное число фотонов для точной локализации центров ФРТ звезд) составляет около часа. Дрожание изображений можно подавлять и методами адаптивной оптики. В разделе 10.1.2 уже отмечалось, что точность порядка 10–4 ² позволяет на удалении в 30 св. лет обнаруживать планеты с массой Юпитера, обращающиеся на расстоянии 5 а. е. от звезды типа Солнца.
Перспективы наземной и космической астрометрии
Два телескопа "Кек" на Мауна-Кеа и четыре телескопа VLT в Чили – это инструменты 8-10-метрового диаметра, установленные в высокогорных обсерваториях и способные работать в режиме интерферометра. В принципе, их можно использовать для астрометрического поиска планет. Телескопам "Кек" для этого еще потребуется некоторая доработка. А с телескопами VLT планируется начать астрометрические измерения уже в 2005 году, используя на каждом из четырех инструментов адаптивную оптику и объединяющую их систему PRIMA (Phase Referenced Imaging and Microarcsecond Astrometry), астрометрическая точность которой будет доведена до 10 микросекунд дуги. Большая полуось орбиты звезды должна быть примерно вдвое больше этого значения, чтобы ее можно было измерить с приемлемой точностью. PRIMA будет способна обнаружить смещения звезды, вызываемые планетой типа Юпитера, на расстояниях до 800 св. лет (уравнение 10.3). Обнаружить присутствие планеты типа Земли она не сможет, но будет способна заметить планету с массой Земли, обращающуюся вокруг маломассивного М-карлика по орбите радиусом несколько а. е., то есть – вне зоны жизни (рис. 8.5). Приблизительно к 2010 году планируется создание системы радиотелескопов миллиметрового диапазона, способной в режиме интерферометра астрометрически обнаруживать планеты. Эта система ALMA (Ataсama Large Millimetre Array) будет располагаться в чилийской пустыне Атакама и состоять из 64 антенн. Достигаемая ею астрометрическая точность (около 10–4 ²) позволит обнаруживать планеты типа Юпитера на расстояниях в десятки световых лет. Хотя интерферометрические и другие измерения с помощью наземных телескопов не позволили пока получить достоверные свидетельства существования экзопланет, однако применение космических телескопов уже привело к первому успеху в этом направлении. В 2002 г. "Хаббл" астрометрически зафиксировал смещение звезды Gliese 876, вызванное обращением вокруг нее нескольких планет-гигантов, причем для измерений использовался не интерферометр, а простой оптический телескоп с одним объективом. Этот успех в значительной мере объясняется небольшой массой звезды Gliese 876 (М-карлик с массой около 1/3 массы Солнца) и тем, что на наличие планет заранее указывали результаты доплеровской спектроскопии (раздел 10.1.4). Астрометрические наблюдения удобнее осуществлять в космосе, поскольку отсутствуют искажения, вызванные земной атмосферой. Большие возможности космической астрометрии продемонстрировал аппарат "Гиппаркос" [Названием спутника служит аббревиатура HIPPARCOS – HIgh Precision PARallax COllecting Satellite, спутник для высокоточных измерений параллаксов. В то же время, оно напоминает нам об античном астрономе Гиппархе (ок. 180 – 125 до н. э.), создавшем первый звездный каталог и открывшем явление прецессии. – Прим. ред. ], запущенный Европейским космическим агентством в 1989 году с программой наблюдений, рассчитанной на четыре года. Точность измерений доходила до 0,0005², что позволяет фиксировать наличие планеты типа Юпитера на расстоянии 30 св. лет.
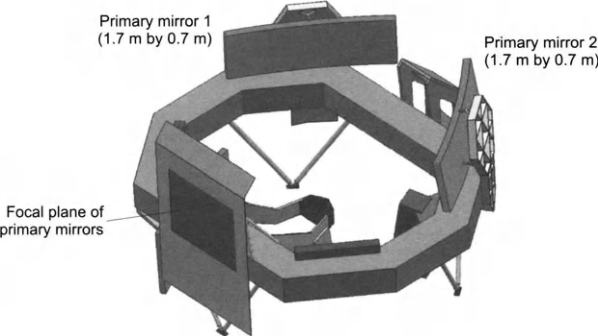
В ближайшем будущем астрометрический поиск планет будет осуществляться несколькими космическими обсерваториями, из которых прежде всего нужно отметить запланированные к запуску в районе 2010 г. аппараты SIM (Space Interferometry Mission, проект NASA) и GAIA (Global Astrometry Instrument for Astrophysics, проект ESA), каждый из которых будет нести по два телескопа. SIM будет измерять отдельные звезды и даст точность в несколько микросекунд дуги даже для слабых звезд, таких как Солнце на расстоянии в несколько тысяч световых лет. Для вычисления орбит столь слабых звезд потребуется провести десятки измерений, для каждого из которых время накопления сигнала составит несколько часов. Планету типа Юпитера можно будет обнаружить на расстоянии несколько тысяч световых лет, а планету типа Земли – на расстоянии несколько десятков световых лет. Но по указанным причинам этот спутник за год сможет исследовать сравнительно немного звезд. Целью запуска европейского спутника GAIA будет исследование не отдельных звезд, а обзор всего звездного неба. Его оптическая схема (рис. 10.7) включает в себя два астрометрических телескопа с главными зеркалами размером 1,7 ´ 0,7 м. Каждый телескоп будет наблюдать свою небольшую область неба, разделенные углом в 106°. Вращение спутника позволит очень точно измерять угловое расстояние (в плоскости вращения) между парами звезд, одновременно попадающими в указанные области неба. Изменив направление вращения спутника, можно измерить углы в другой плоскости и окончательно вычислить полные угловые расстояния между звездами. За 5 лет запланированной работы спутника каждый участок звездного неба будет просканирован около 80 раз. Для звезд с визуальной величиной не слабее 10 m (так выглядит Солнце с расстояния 350 св. лет) точность измерения большой полуоси орбиты (в проекции на небо) составит около 40 микросекунд дуги. Этого достаточно для обнаружения рядом с М-карликом планеты типа Юпитера с расстояния 350 св. лет или планеты с массой несколько масс Земли с расстояния несколько десятков световых лет. Но планету с массой Земли заметить не удастся. Третий телескоп на спутнике GAIA предназначен для измерения лучевых скоростей звезд. Хотя точность этого прибора представляется недостаточной для обнаружения планет, однако сам метод доплеровской спектроскопии, описанный в следующем разделе, дает такую возможность.
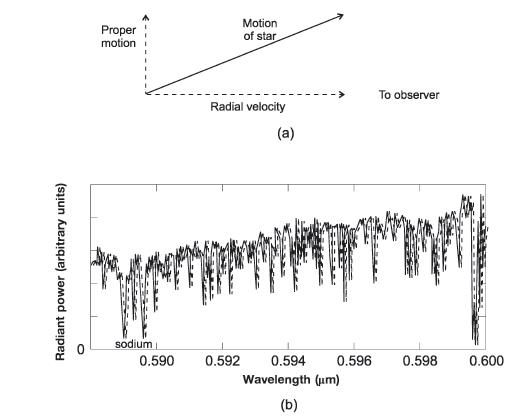
10.1.4. Доплеровская спектроскопия: теория
В отличие от астрометрии, позволяющей обнаруживать орбитальное движение звезды путем точных измерений ее положения в последовательные моменты времени, доплеровская спектроскопия дает возможность выявлять орбитальное движение путем многократного измерения лучевой скорости звезды, то есть компонента полной скорости, направленного вдоль луча зрения наблюдателя (рис. 10.8(а)). Поэтому такой метод иногда называют методом лучевых скоростей. Обнаружив циклическое изменение лучевой скорости звезды, мы можем предположить, что звезда имеет орбитальное движение, следовательно, рядом с ней есть компаньон. Лучевую скорость измеряют по положению линий в спектре звезды. На рис. 10.8(б) представлен спектр звезды с многочисленными линиями поглощения (узкие участки спектра, в которых излучение значительно ослаблено). Эти линии возникают в атмосфере звезды, в основном состоящей из водорода и гелия, но содержащей и другие, редкие, но важные химические элементы.
Рис 10.8 Большинство элементов представлено одиночными атомами, часть из которых ионизована (большая или меньшая – в зависимости от элемента и температуры звезды). В атмосферах наиболее холодных звезд могут существовать простые молекулы. Излучение звезды просачивается из недр наружу сквозь атмосферу. Ее атомы поглощают проходящее излучение со строго определенными длинами волн, характерными для каждого элемента. Большая часть поглощенной энергии затем вновь излучается с той же длиной волны, но уже во всех направлениях. Некоторая часть энергии излучается на больших длинах волн, а остаток рассеивается при столкновениях атомов друг с другом. Именно эта столкновительная деактивация атомов поддерживает температуру в атмосфере звезды. Столкновения могут возбуждать атомы, которые затем излучают на характерных длинах волн. Каждый химический элемент в атмосфере звезды проявляет себя наличием в спектре либо линий поглощения (как показано на рисунке), либо линий излучения (эмиссионных линий – узких областей спектра, в которых наблюдается избыток излучения). Оба типа линий имеют строго определенные длины волн для каждого элемента, что позволяет легко идентифицировать излучающие атомы. В доплеровской спектроскопии обычно используют линии поглощения, которых, как правило, значительно больше. Лучевую скорость звезды определяют по спектральным линиям, используя эффект Доплера. Он заключается в том, что измеренная наблюдателем длина волны излучения любого источника зависит от лучевой скорости этого источника относительно наблюдателя. Именно поэтому линии в наблюдаемом спектре звезды (рис. 10.8(б)) несколько сдвинуты, что показывает пунктирная линия. Изменения относятся лишь к измеряемым значениям длин волн, а не к истинным их значениям, которые естественно не зависят от движения источника в пространстве. Отметим, что собственное движение звезды (поперечный компонент скорости) не вызывает смещения линий. Изменение регистрируемой наблюдателем длины волны зависит только от лучевого компонента скорости звезды nr и определяется формулой
lнабл – lисточ nr = с ------------------ (10.7) lисточ
где с – скорость волны (в нашем случае равная скорости света), lисточ – длина волны излучения источника, а lнабл – длина волны, воспринимаемая и регистрируемая наблюдателем. Если lнабл > lисточ, то источник удаляется от наблюдателя. В этом случае, как указывает уравнение (10.7), лучевая скорость nr имеет положительное значение. Мы не приводим вывода формулы (10.7), поскольку он содержится во многих учебных курсах, включая ук
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 588; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.015 с.) |


 (10.3),
(10.3),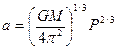 (10.4).
(10.4).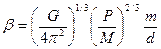 (10.5).
(10.5).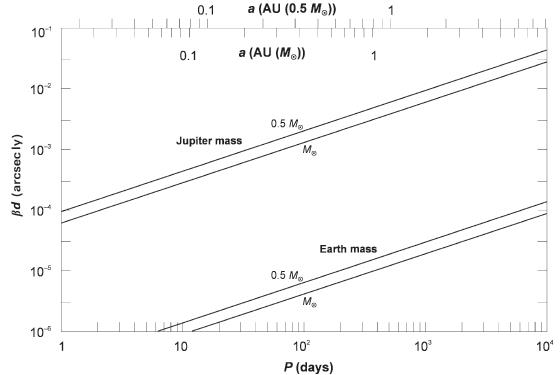
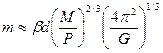 (10.6)
(10.6)