
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гравитационное микролинзированиеСодержание книги
Поиск на нашем сайте
Рис 10.17
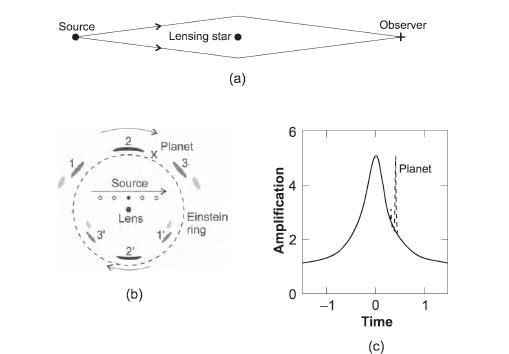
В этом методе используется эффект гравитационного влияния экзопланетной системы на проходящий через неё свет более далекой, фоновой звезды, которую чаще называют просто "источником". На рис. 10.7(а) показано взаимное расположение на одной линии источника, наблюдателя и находящейся между ними звезды, у которой могут быть планеты. На первый взгляд кажется, что источник скрыт от наблюдателя. Но гравитационное поле расположенной между ними звезды искривляет траектории световых лучей и позволяет им попасть к наблюдателю (поэтому звезду в этом случае часто называют "гравитационной линзой"). В результате наблюдатель видит источник в форме кольца вокруг изучаемой звезды. Это кольцо называют "кольцом Эйнштейна", в честь Альберта Эйнштейна, чья общая теория относительности (1916) позволила объяснить искривление световых лучей гравитацией. Кольцо, показанное фронтально на рис. 10.7(б), имеет угловой радиус
где M – масса линзы, а dl и d s – расстояния от наблюдателя до звезды-линзы и звезды-источника, соответственно. При типичных значениях всех параметров величина q Е равна нескольким сотням микросекунд дуги. Сравним это с угловым радиусом центрального диска дифракционно-ограниченной ФРТ, равным 1,22l/ D радиан (уравнение 9.1). При длине волны l = 0,5 мкм и апертуре телескопа D около 10 метров радиус диска составляет 1,3 ´ 104 микросекунд дуги, поэтому телескоп не сможет дать изображение кольца. Однако эффект гравитационной линзы всё же удается зарегистрировать, поскольку при его наличии мы получаем от звезды большее света, чем при его отсутствии. Таким образом, когда собственное движение изучаемой звезды подводит ее на небе близко к звезде-источнику, мы должны обнаружить увеличение яркости этой «линзированной» звезды. Этот эффект временного увеличения яркости называют гравитационным микролинзированием. Конечно, звезды никогда не располагаются абсолютно точно вдоль прямой линии. На рис. 10.17(б) показана последовательность взаимного расположения двух звезд на небе, когда угловое расстояние между ними описывается изменяющейся долей x введенного выше углового радиуса q Е кольца. При таком прохождении линзовый эффект создает последовательность искаженных парных изображений, например, приведенных на рисунке комбинаций (1, 1¢), (2, 2¢) и (3, 3¢), располагающихся вблизи кольца Эйнштейна. Коэффициент А усиления блеска источника из-за линзового эффекта (показан на рис.10.17(в) сплошной линией) описывается уравнением
и зависит только от x; пик кривой, естественно, соответствует наиболее тесном сближению на небе линзы и источника. Если сближение происходит лишь до расстояния много большего q Е, когда x» 1, то усиления практически не наблюдается (А» 1). По порядку величины длительность линзового эффекта составляет
где m – собственное движение линзы относительно источника (в единицах угла за единицу времени). При стандартных значениях параметров время t E составляет несколько суток. Линзовый эффект может возникнуть и под влиянием гравитационного поля планеты, причем любой массы. Поскольку пиковое усиление зависит только от x (уравнение 10.15), при достаточно малых значениях x планета может создать усиление, сравнимое с усилением звезды. К сожалению, q Е пропорционально квадратному корню из значения массы линзы (уравнение 10.14), поэтому площадь области усиления от планеты очень мала, и требуется чрезвычайно точное ее совпадение с одним из изображений источника, чтобы эффект стал заметным. К тому же, продолжительность усиления также пропорциональна квадратному корню из массы (уравнение 10.16), так что даже при самом благоприятном расположении планеты длительность усиления ею яркости источника ограничена часами или даже минутами; это событие легко можно пропустить. Поэтому на практике пытаются заметить момент начала гравитационного линзирования звездой и затем тщательно следить за ней, пытаясь не пропустить возможный кратковременный эффект от планеты. Это возможно лишь в том случае, когда орбита планеты проходит вблизи траектории одного из изображений звезды-источника (на рис. 10.17(б) это положение планеты обозначено значком «´»). Тогда гравитационное поле планеты сможет отклонить лучи света, создающие изображение источника, и создать на кривой блеска резкий пик, показанный пунктиром на рис.10.17(в). Высота пика возрастает с приближением планеты к изображению источника, поскольку коэффициент ее усиления определяется тем же уравнением (10.15), где роль относительного расстояния играет ее удаленность от изображения. Поэтому пик может быть высоким, а его длительность t Eр порядка q Ер/m, где q Ер – угловой радиус кольца Эйнштейна для планеты. Отсюда следует соотношение:
где m – масса планеты, так что длительность наблюдаемого линзового эффекта возрастает с увеличением массы планеты. Предположим, что орбита планеты действительно располагается вблизи траектории одного из изображений звезды-источника, а сами эти траектории лежат близко к кольцу Эйнштейна. В этом случае угловое расстояние между планетой, которую мы хотим обнаружить, и ее звездой должно быть таким, чтобы в проекции на небо оно примерно равнялось угловому радиусу q Е кольца от звезды, а планета при этом еще и располагалась бы на орбите в точно требуемом для обнаружения линзового эффекта месте. Понятно, что таким способом можно выявить лишь весьма незначительное число экзопланет. Тем не менее, микролинзирование считается ценным дополнительным методом по нескольким причинам. Во-первых, он позволяет обнаруживать планеты на очень больших расстояниях, вплоть до десятков тысяч световых лет, что значительно превышает возможности доплеровской спектроскопии и фотометрии прохождений. Во-вторых, он позволяет определять массу планеты, причем даже очень небольшую массу m из уравнения (10.17) в тех случаях, когда мы можем каким-либо независимым способом оценить массу звезды M. Более того, поскольку длительность события пропорциональна m ½, ширина пика при прохождении планеты с массой Земли будет всего в 318½ = 18 раз меньше, чем для планеты с массой Юпитера, так что линзовый эффект позволяет обнаруживать даже очень маленькие планеты. В-третьих, нам не нужно проводить измерения в течение всего периода обращения планеты, то есть для планеты типа Юпитера (с радиусом орбиты 5 а. е.) измерения займут всего несколько дней, а не несколько лет. Наконец, регистрируя побочные пики блеска, мы можем обнаружить даже спутники у планет. С другой стороны, у метода микролинзирования есть и свои минусы. Во-первых, он почти не дает информации об орбите планеты. Фактически, мы знаем, что в момент наблюдения угловое расстояние между звездой и планетой приблизительно равно q Е, что в линейной мере составляет R E = dlq Е, где величину R E можно назвать линейным радиусом кольца Эйнштейна. Обычно значение R E составляет несколько астрономических единиц. Так что все, что мы узнаем об орбите планеты, это что в момент наблюдения проекция расстояния от звезды до планеты составляла несколько а. е. Кроме того, гравитационное микролинзирование – это почти всегда «разовое» явлением, повторение такого события крайне маловероятно. Так что для достаточно близких систем измерения по этому методу полезно сочетать с другими, описанными выше методами. Предпринято уже довольно много обзоров по поиску микролинзорования. В основном исследовались те участки неба, где велика плотность звезд фона, играющих роль источников, и много более близких звезд, способных играть роль гравитационных линз. Такой областью, например, является центральный балдж Галактики (разд. 1.3.2). Множество событий микролинзирования было зарегистрировано в многолетнем обзоре OGLE (Optical Gravitational Lensing Experiment) с использованием 1,3-метрового телескопа «Варшава» на обсерватории Лас-Кампанас (Чили). Особенно важно быстро оповещать о таких событиях другие обсерватории, чтобы не пропустить кратковременные планетные события. Системы быстрого оповещения сейчас создаются, и можно лишь сожалеть, что ранее из-за их отсутствия мы получили лишь разрозненные и недостаточно достоверные свидетельства о существовании нескольких экзопланет.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 683; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |


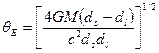 (10.14),
(10.14),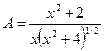 (10.15)
(10.15) (10.16)
(10.16) (10.17)
(10.17)


