
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ввести массив NxN (не больше 50) целых чисел и в функции посчитать сумму его положительных значений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте #include <stdio.h> #include <conio.h> void summa(int, int a1[ ][50]);
void main(void) { int a[50][50]; int i,j,N; clrscr(); puts("\n Введите размер массива N (<50)\n"); scanf(“%d”,&N); printf("\n Введите данные \n"); for(i=0; i<N; i++) for(j=0; j<N; j++) { printf("\n a[%d][%d]=", i+1, j+1); scanf("%d", &a[i][j]); } summa(N,a); } void summa(int n, int a1[ ][50]) { int i,j,s; puts(" ФУНКЦИЯ summa "); /* ВЫЧИСЛЕНИЕ СУММЫ ПОЛОЖИТЕЛЬНЫХ ЭЛЕМЕНТОВ МАССИВА */ for (s=0,i=0; i<n; i++) { printf("\n"); for (j=0;j<n;j++) if (a1[i][j]>0) s+=a1[i][j]; } printf("\a СУММА = %d, Press any key... ",s); getch(); }
Варианты индивидуальных заданий 1. Даны три натуральных числа. Определить их наибольший делитель (определение HOD – см. N 10). 2. Даны отрезки a,b,c,d. Для каждой тройки этих отрезков, из которых можно построить треугольник, вычислить площади треугольников. Площадь треугольника 3. Дано натуральное число N. Определить, если это возможно, пару x,y таких натуральных чисел, что 4. Дано натуральное число N. Определить все пары x,y натуральных чисел таких, что 5. Даны действительные числа x,y (x>0, y>1). Получить целое число K (положительное, отрицательное или равное нулю), удовлетворяющее условию 6. Дано натуральное число N (N > 99). Определить число сотен в нем. 7. Дано натуральное число N (N 8. Дано натуральное число N (N > 10000). Определить сумму цифр первых K разрядов числа N (K 9. Даны натуральные числа n,m. Получить произведение m последних цифр числа n. 10. Даны натуральные числа n,m. Найти наибольший общий делитель n и m (наименьшее общее кратное n и m) используя алгоритм Евклида. Пусть n и m – одновременно не равные нулю целые неотрицательные числа и пусть m 11. Даны натуральные числа a,b,c,d. Вычислить f(a)·f(b)+f(c)
12. Дано натуральное число N. Удалить из записи числа N цифры 0 и 5, оставив прежним порядок остальных цифр. Например, из числа 59015509 должно получиться число 919. 13. Дано натуральное число N. Получить все такие натуральные K, что N делится на K2 и не делится на K3. 14. Даны натуральные целые числа n и m, вычислить A(n,m), где
15. Натуральное число из n цифр является числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу (как, например, 153=13+53+33 ). Получить все числа Армстронга, состоящие из двух, трех и четырех цифр. 16. Имеется n населенных пунктов, перенумерованных от 1 до n (n=10). Некоторые пары пунктов соединены дорогами. Определить, можно ли попасть по этим дорогам из первого пункта в n-й пункт. Информация о дорогах задается в виде последовательности пар чисел i и j (i<j) указывающих, что i-й и ј-й населенный пункт пункты соединены дорогой. Признак окончания этой последовательности – пара нулей. 17. Напечатать все цифры числа 2500 и числа 1!+2!+…+100! 18. Даны координаты вершин двух треугольников. Определить, какой из них имеет большую площадь. 19. Три прямые на плоскости заданы уравнением akx+bky=ck (k=1,2,3). Если эти прямые попарно пересекаются и образуют треугольник, тогда найти его площадь. 20. Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, числа 41 и 43). Напечатать все пары «близнецов» на отрезке [n,2n], где n – заданное целое число, больше 2. 21. Ввести целое натуральное число N. Сформировать треугольник Паскаля по алгоритму: C00 C10 C11 C20 C21 C22 C30 C31 C32 C33 C40 C41 C42 C43 C44 ……………………….. Здесь 22. «Ханойская башня». Имеются три колышка A,B и C и n дисков разного размера, перенумерованных от 1 до n в порядке возрастания их размеров. Сначала все диски надеты на колышек A так, как показано на рис.1,а. Требуется перенести все диски с колышка A на колышек С (рис.1,в), соблюдая при этом следующие условия:диски можно переносить только по одному, больший диск нельзя ставить на меньший. 23.
А В С А В С А В С а) б) с)
Рис. 1
24. «Задача о 8 ферзях». На шахматной доске расставить 8 ферзей так, чтобы они не «били» друг друга (всего существует 92 расстановки). 25.«Метод фон Неймана». Дано n вещественных чисел. Упорядочить их по неубыванию:образовать два массива А и В и записать исходные числа в А; упорядочить пары соседних чисел (А1 и А2, А3 и А4 и т.д.) и записать их в В; взять из В по две соседние упорядоченные пары и, слив их в упорядоченные четверки, снова записать в А; затем каждые две соседние четверки из В слить в упорядоченные восьмерки и перенести в А, и т.д. 26. Даны два массива чисел X и Y размером 100 элементов. Составить программу меняющую последовательно местами значение элементов xk и yk не используя промежуточных величин. 27. Дана последовательность из N целых чисел, среди которых нет двух одинаковых. Требуется вычеркнуть минимально возможное количество чисел так, чтобы оставшиеся числа шли в порядке возрастания. 28. Имеется 9 карточек, на которых написаны цифры 1,2,3,4,5,6,7,8,9 (по одной цифре на каждой карточке). Из этих карточек составляются два числа. Первое число – это числитель дроби, а второе число – это знаменатель дроби. Каждая карточка должна быть обязательно использована. Знаменатель дроби состоит из пяти цифр. Например, числитель – 6729, знаменатель – 13458 (все карточки использованы). Дробь 6729/13458 в точности равна ½. 29. Ввести два натуральных числа N и M. Найти такую комбинацию карточек (если она существует), которая образовала бы дробь, равную в точности N/M. Если комбинация не единственная, то вывести их все.
Контрольные вопросы 1. Чем функция пользователя отличается от стандартной функции? 2. Способы передачи аргументов в функцию? 3. Поясните понятие “локальные” и “глобальные” переменные? 4. Для чего и каким образом применяется оператор return?
ЛАБОРАТОРНАЯ РАБОТА № 6
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.006 с.) |

 , где
, где 
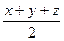 .
.
 .
. ,
,  .
. <
<  .
. 99).Выяснить, верно ли, что N2 равно кубу суммы цифр числа N.
99).Выяснить, верно ли, что N2 равно кубу суммы цифр числа N. n. Тогда, если n = 0, то NOD (n,m) = m, и если n ≠ 0, то для чисел m, n, r, где r остаток от деления m на n, выполняется равенство NOD (m,n) = NOD (n,r). Например, NOD (15,6) = NOD (6,3) = NOD (3,0) = 3.
n. Тогда, если n = 0, то NOD (n,m) = m, и если n ≠ 0, то для чисел m, n, r, где r остаток от деления m на n, выполняется равенство NOD (m,n) = NOD (n,r). Например, NOD (15,6) = NOD (6,3) = NOD (3,0) = 3. f(d), где
f(d), где

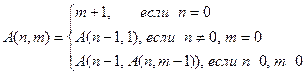
 , где n!=1·2·3·….·n – факториал числа n.
, где n!=1·2·3·….·n – факториал числа n.


 Написать программу, которая печатает последовательность действий (в виде «перенести диск с q на r», где q и r – это А,В или С), решающую указанную задачу для n дисков, где n- заданное натуральное число. (При правильном переносе n дисков с А на С обязательно встретится конфигурация, показанная на рис.6,б).
Написать программу, которая печатает последовательность действий (в виде «перенести диск с q на r», где q и r – это А,В или С), решающую указанную задачу для n дисков, где n- заданное натуральное число. (При правильном переносе n дисков с А на С обязательно встретится конфигурация, показанная на рис.6,б).












