Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производственная функция и ее свойстваСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Ранее было показано, что представление производственной системы в виде «черного ящика» предполагает установление связи между факторами производства и продуктом с помощью функциональной зависимости, называемой производственной функцией (ПФ). Существует строгое математическое определение ПФ: ПФ – это уравнение гиперповерхности эффективных технологических процессов, а именно - это непрерывная дифференцируемая функция v=f(u), описывающая множество эффективных технологических процессов. Другими словами эта функция однозначно определяет наибольший набор продуктов v, который может быть произведен для определенного набора факторов u. Агрегирование наборов факторов и продуктов производства позволяет привести уравнение гиперповерхности к виду:
Отметим, что под агрегированием понимают операции укрупнения (суммирования) объемов факторов и продуктов, если они являются однородными товарами, либо стоимостное соизмерение разнородных товаров (индексы в статистике!). Также ПФ могут определены для систем различных масштабов – от производственных участков до мировой экономики. Вопросы получения различных видов математических зависимостей в ПФ основаны на эконометрике и регрессионном анализе. Фактически речь идет о построении простых или множественных уравнений регрессии. Так, распространенной в анализе производственных процессов является производственная функция, связывающая объем выпуска единственного продукта (Y) с агрегированными факторами труда (L) и капитала (К) за определенный период времени: Y = f(L,K). Отметим, что с точки зрения управленческого учета затраты труда представляют переменные издержки, а затраты капитала – постоянные издержки производства. Поэтому в краткосрочном периоде система производства может изменять только затраты труда, но не может изменить затраты капитала. Следовательно, изменение обоих факторов возможно только в долгосрочном периоде. Рассмотрим общие свойства ПФ: 1. Это свойство означает (аналогично первому свойству технологических множеств), что при отсутствии затрат одного из факторов производства производится нулевой продукт, то есть не существует факторов – абсолютных субститутов. То есть возможно лишь частичное замещение одного фактора другим, а не полное. Для двухфакторной ПФ соответственно это свойство будет означать: f(L,0)=0 и f(0,K)=0. 2. Фактически это свойство означает, что производительность любой системы ограничена сверху, то есть при увеличении затрат факторов количество производимого продукта будет расти, а после достижения некоторого критического значения будет падать. Критические значения и задают границу экономической области, выход из которой приводит к снижению производительности системы при дальнейшем росте факторов производства. Следовательно, на границе экономической области существуют такие точки, в которых 3. Это свойство означает вогнутость ПФ, а с экономической точки зрения оно выражает закон убывания предельной эффективности производства продукта при увеличении затрат факторов (см. закон убывания предельной полезности в модели потребителя). 4. - это свойство характеризует линейную однородность ПФ, то есть при одновременном изменении количества затрат факторов в l раз, количество произведенного продукта изменится также в l раз. Свойство линейной однородности позволяет также преобразовать ПФ в функцию одной переменной. Например, двухфакторную ПФ можно привести к однофакторной:
Или: ПФ, которые обладают всеми приведенными выше свойствами, называют неоклассическими. Рассмотрим подробнее свойства неоклассических ПФ. Ранее было сформулировано положение о том, что ПФ строится на множестве эффективных технологических процессов. Математически эффективность производственного процесса определяется величиной среднего и предельного продуктов, произведенных при определенных затратах факторов производства. Средний продуктi -го фактора производства – это есть отношение количества произведенного продукта к количеству затрачиваемого фактора xi за период времени: Предельный продукт фактора xi – это дополнительный продукт, произведенный системой при затратах дополнительной единицы фактора xi. Опять-таки, можно провести аналогию между понятиями предельный продукт и предельная полезность, качественная однородность этих понятий приводит к понятию первой частной производной продукта y по затратам фактора xi как количественной мере оценки этой предельной величины:
Отношение предельного продукта к среднему дает коэффициент эластичности продукта по i -му фактору производства (аналогично коэффициенту эластичности функции спроса по доходу):
Для двухфакторной ПФ имеем:
Коэффициент эластичности продукта по i- му фактору показывает, на сколько процентов изменится количество произведенного продукта при увеличении затрат i -го фактора на один процент. Используя коэффициенты эластичности можно выразить предельный продукт через средний:
Введение коэффициентов эластичности позволяет вычислить изменение выпуска продукта при одновременном изменении объемов затрачиваемых факторов:
Последнее свойство ПФ об однородности приводит также к понятию степени однородности ПФ, а именно:
В общем случае, для любой однородной дифференцируемой функции со степенью однородности δ справедлива теорема Эйлера:
Для двухфакторной ПФ, являющейся линейно-однородной (δ=1) теорема Эйлера приводит к:
Если бы двухфакторная ПФ не являлась бы линейно-однородной, то тогда справедливо соотношение:
И в заключение обсуждения свойств ПФ рассмотрим, как влияет изменение масштаба производства на его эффективность. Для этого вводятся понятия среднего и предельного продукта масштаба производства. Средний продукт масштаба – это есть отношение продукта, полученного при увеличении факторов в l раз, к коэффициенту масштабирования l:
Предельный продукт масштаба производства приблизительно равен частной производной продукта, полученного при увеличении факторов в l раз по коэффициенту масштабирования:
Так как коэффициент эластичности – это отношение предельного продукта к среднему, то коэффициент эластичности масштаба производства будет равен:
И еще одно важное свойство El: для любой однородной ПФ сумма коэффициентов эластичности продукта по факторам равна коэффициенту эластичности масштаба производства:
Анализ коэффициента эластичности масштаба производства позволяет выявить, что если El >1, то укрупнение производства дает положительный эффект, так как такие производственные системы имею более высокую эффективность при увеличении масштабов производства. Если El <1, то увеличение масштаба производства приведет к снижению его эффективности, но уменьшение масштаба в этом случае даст повышение производительности системы. Для линейно-однородных ПФ изменение масштабов производства приводит всегда к пропорциональному изменению продукта, то есть производство инвариантно к изменению масштаба.
Изокванты и изоклины ПФ Если вновь обратиться к методу аналогии, то, как и в случае модели поведения потребителя, в теории моделирования производственных процессов можно выделить понятие кривой безразличия производителя. Этому понятию может соответствовать множество наборов производственных факторов, которым соответствует одинаковое количество произведенного продукта, то есть:
Множество точек, удовлетворяющих равенству (4.1), называют изоквантой ПФ (iso – постоянный, quantity – количество). Каждая изокванта соответствует различному уровню производства продукта (y), причем изокванты, более удаленные от нулевой точки (точки бездействия) соответствуют более высоким значениям y. Изокванты также обладают теми же свойствами, что и кривые безразличия (параллельны друг другу, не пересекаются с осями абсцисс и ординат и др.) Для двухфакторной ПФ изокванта по сути будет выражать функциональную зависимость затрат капитала от затрат труда при данном уровне произведенного продукта:
Производитель, варьируя технологии, может выбирать разные сочетания факторов производства и поддерживать при этом постоянный уровень производства. Согласно изокванте, увеличение одного фактора приведет к уменьшению другого. Следовательно, должна существовать характеристика, позволяющая оценить компенсацию одного фактора другим. Такой характеристикой является предельная норма замещения (аналогично такой же характеристике в теории полезности потребителя):
которая показывает, какое увеличение фактора j скомпенсирует снижение фактора i на единицу, чтобы уровень производства продукта остался прежним (замещение фактора i фактором j). Соответственно обратное замещение (фактора j фактором i) будет характеризоваться обратной величиной: Согласно взаимосвязи коэффициента эластичности и предельного продукта (4.1) предельную норму замещения можно выразить как:
Согласно (4.1) для двухфакторной ПФ имеем:
Согласно (4.3) для двухфакторной модели также предельную норму замещения можно выразить через коэффициенты эластичности:
Наряду с изоквантами важную роль в ПФ играют изоклины – множества точек экономической области, у которых предельная норма замещения i -го фактора j -м постоянна:
Используя понятие изоклины (изоклинали) можно преобразовать произвольный набор факторов (L,K) в набор (Y,MRS), то есть решением системы уравнений:
будет являться:
Однородная ПФ с постоянной предельной нормой замещения труда капиталом и степенью однородности δ=1 относится к классу линейных функций, то есть Таким образом, для двухфакторной ПФ каждая точка изокванты характеризуется затратами капитала и труда или предельной нормой замещения труда капиталом MRSLK и фондовооруженностью k. Если обратиться к геометрическому представлению, то MRSLK равна угловому коэффициенту касательной к данной точке изокванты, а величина k – угловому коэффициенту луча, выходящего из начала координат и проходящего через заданную точку изокванты (см. Рис. 4.2).
Рис 4.2
Таким образом, очевидной становится связь между изменением фондовооруженности и предельной нормой замещения труда капитала, то есть мы опять приходим к понятию эластичности, а именно эластичности замещения труда капиталом, которая показывает, насколько процентов изменится фондовооруженность труда при изменении предельной нормы замещения труда капиталом на один процент:
Рис 4.3 Отметим, что в обоих случаях в точках А и В значения MRSLK остаются одинаковыми, а значение фондовооруженности в точке А выше, чем в точке В. Отсюда вытекает еще одно важное свойство: для однородной ПФ эластичность замещения труда капиталом зависит лишь от фондовооруженности и остается постоянной вдоль лучей, выходящих из нулевой точки. Выразим связь между MRSLK и k при постоянной эластичности Eσ. Согласно (4.4) имеем:
Предполагая зависимость MRSLK(k), можно записать (4.5) в виде обычного дифференциального уравнения:
Интегрирование (4.6) дает:
Следовательно, условие постоянства эластичности замещения труда капиталом дает степенную зависимость между величинами MRSLK и k. Соответственно, случай единичной эластичности будет соответствовать линейной связи между указанными величинами:
Введение понятия постоянной эластичности замещения привело к общей форме однородной ПФ, для которой эластичность замещения факторов постоянна. Такие ПФ называют ПФ класса CES (Constant Elasticity of Substitution). Впервые функции этого класса были предложены Эрроу Кеннетом и Солоу Робертом в 1961 году. Функции этого класса предполагают, что замещение труда капиталом возможно только в некоторых пределах и не существует технологий, которые позволяли бы произвести заданное количество продукта при затратах факторов производства ниже определенных критических значений. (Геометрически это означает, что можно построить асимптоты к изокванте, и они будут соответствовать минимально возможным значениями труда и капитала. Возможен вывод математических соотношений асимптот, в данном изложении этот материал мы не будем приводить.) Многие ПФ являются по сути частными или предельными случаями функций CES, основные характеристики которых приведены в Табл 4.1. Табл 4.1
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

 , то есть связь (эффективное преобразование) между агрегированными факторами производства и единственным продуктом.
, то есть связь (эффективное преобразование) между агрегированными факторами производства и единственным продуктом.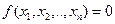 при xi=0 для любых
при xi=0 для любых 
 для всех
для всех  .(??), а количество производимого продукта при увеличении факторов производства будет расти внутри экономической области.
.(??), а количество производимого продукта при увеличении факторов производства будет расти внутри экономической области. для всех
для всех 
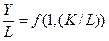 или
или  , где y – средняя производительность труда, к – фондовооруженность.
, где y – средняя производительность труда, к – фондовооруженность. . Для двухфакторной ПФ можно получить соотношения:
. Для двухфакторной ПФ можно получить соотношения:  и
и  , что соответствует средней фондоотдаче (среднему количеству произведенного продукта единицей капитала) и средней производительности труда (среднему количеству произведенного продукта единицей труда). (Можно провести аналогию с моделированием потребителя). Понятие среднего продукта является подтверждением вогнутости ПФ: чем больше затраты по фактору, тем меньше средний продукт.
, что соответствует средней фондоотдаче (среднему количеству произведенного продукта единицей капитала) и средней производительности труда (среднему количеству произведенного продукта единицей труда). (Можно провести аналогию с моделированием потребителя). Понятие среднего продукта является подтверждением вогнутости ПФ: чем больше затраты по фактору, тем меньше средний продукт. , а для двухфакторной ПФ:
, а для двухфакторной ПФ:  и
и  , что соответствует предельной фондоотдаче и предельной производительности труда (marginal product of capital, marginal product of labor). Опять-таки, предельные продукты факторов всегда меньше средних продуктов, что является следствием вогнутости ПФ.
, что соответствует предельной фондоотдаче и предельной производительности труда (marginal product of capital, marginal product of labor). Опять-таки, предельные продукты факторов всегда меньше средних продуктов, что является следствием вогнутости ПФ.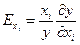
 и
и 

 или
или  (4.1)
(4.1)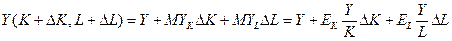
 , где δ – степень однородности ПФ. Неоклассическая ПФ является однородной ПФ со степенью однородности, равной единице. Такие функции называют также линейно-однородными.
, где δ – степень однородности ПФ. Неоклассическая ПФ является однородной ПФ со степенью однородности, равной единице. Такие функции называют также линейно-однородными. . Эта теорема имеет важное экономическое значение, а именно, произведенный продукт может быть представлен как сумма вкладов каждого фактора в произведенный продукт.
. Эта теорема имеет важное экономическое значение, а именно, произведенный продукт может быть представлен как сумма вкладов каждого фактора в произведенный продукт. .
. , отсюда следует, что:
, отсюда следует, что:


 , то есть коэффициент эластичности масштаба производства всегда будет равен степени однородности ПФ.
, то есть коэффициент эластичности масштаба производства всегда будет равен степени однородности ПФ.


 , (4.2)
, (4.2) .
. (4.3)
(4.3) - предельная норма замещения капитала трудом;
- предельная норма замещения капитала трудом; - предельная норма замещения труда капиталом.
- предельная норма замещения труда капиталом.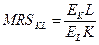
 , где к – фондовооруженность.
, где к – фондовооруженность.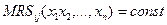
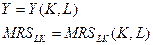

 .
. Например, в точке В значение затрат труда больше, чем в точке А, следовательно, значение MRSLK в точке В меньше, чем в точке А. Соответственно точка В будет соответствовать меньшему значению фондовооруженности, чем в точке А.
Например, в точке В значение затрат труда больше, чем в точке А, следовательно, значение MRSLK в точке В меньше, чем в точке А. Соответственно точка В будет соответствовать меньшему значению фондовооруженности, чем в точке А. (4.4)
(4.4) Графически можно также показать, что с ростом кривизны изокванты эластичность Eσ уменьшается (см. Рис. 4.3).
Графически можно также показать, что с ростом кривизны изокванты эластичность Eσ уменьшается (см. Рис. 4.3).
 (4.5)
(4.5) (4.6)
(4.6) или после преобразования:
или после преобразования: , где
, где