
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие производственной системы и производственного процесса. Технологический процесс и технологическое множествоСодержание книги
Поиск на нашем сайте
Изокванты и изоклины ПФ Если вновь обратиться к методу аналогии, то, как и в случае модели поведения потребителя, в теории моделирования производственных процессов можно выделить понятие кривой безразличия производителя. Этому понятию может соответствовать множество наборов производственных факторов, которым соответствует одинаковое количество произведенного продукта, то есть:
Множество точек, удовлетворяющих равенству (4.1), называют изоквантой ПФ (iso – постоянный, quantity – количество). Каждая изокванта соответствует различному уровню производства продукта (y), причем изокванты, более удаленные от нулевой точки (точки бездействия) соответствуют более высоким значениям y. Изокванты также обладают теми же свойствами, что и кривые безразличия (параллельны друг другу, не пересекаются с осями абсцисс и ординат и др.) Для двухфакторной ПФ изокванта по сути будет выражать функциональную зависимость затрат капитала от затрат труда при данном уровне произведенного продукта:
Производитель, варьируя технологии, может выбирать разные сочетания факторов производства и поддерживать при этом постоянный уровень производства. Согласно изокванте, увеличение одного фактора приведет к уменьшению другого. Следовательно, должна существовать характеристика, позволяющая оценить компенсацию одного фактора другим. Такой характеристикой является предельная норма замещения (аналогично такой же характеристике в теории полезности потребителя):
которая показывает, какое увеличение фактора j скомпенсирует снижение фактора i на единицу, чтобы уровень производства продукта остался прежним (замещение фактора i фактором j). Соответственно обратное замещение (фактора j фактором i) будет характеризоваться обратной величиной: Согласно взаимосвязи коэффициента эластичности и предельного продукта (4.1) предельную норму замещения можно выразить как:
Согласно (4.1) для двухфакторной ПФ имеем:
Согласно (4.3) для двухфакторной модели также предельную норму замещения можно выразить через коэффициенты эластичности:
Наряду с изоквантами важную роль в ПФ играют изоклины – множества точек экономической области, у которых предельная норма замещения i -го фактора j -м постоянна:
Используя понятие изоклины (изоклинали) можно преобразовать произвольный набор факторов (L,K) в набор (Y,MRS), то есть решением системы уравнений:
будет являться:
Однородная ПФ с постоянной предельной нормой замещения труда капиталом и степенью однородности δ=1 относится к классу линейных функций, то есть Таким образом, для двухфакторной ПФ каждая точка изокванты характеризуется затратами капитала и труда или предельной нормой замещения труда капиталом MRSLK и фондовооруженностью k. Если обратиться к геометрическому представлению, то MRSLK равна угловому коэффициенту касательной к данной точке изокванты, а величина k – угловому коэффициенту луча, выходящего из начала координат и проходящего через заданную точку изокванты (см. Рис. 4.2).
Рис 4.2
Таким образом, очевидной становится связь между изменением фондовооруженности и предельной нормой замещения труда капитала, то есть мы опять приходим к понятию эластичности, а именно эластичности замещения труда капиталом, которая показывает, насколько процентов изменится фондовооруженность труда при изменении предельной нормы замещения труда капиталом на один процент:
Рис 4.3 Отметим, что в обоих случаях в точках А и В значения MRSLK остаются одинаковыми, а значение фондовооруженности в точке А выше, чем в точке В. Отсюда вытекает еще одно важное свойство: для однородной ПФ эластичность замещения труда капиталом зависит лишь от фондовооруженности и остается постоянной вдоль лучей, выходящих из нулевой точки. Выразим связь между MRSLK и k при постоянной эластичности Eσ. Согласно (4.4) имеем:
Предполагая зависимость MRSLK(k), можно записать (4.5) в виде обычного дифференциального уравнения:
Интегрирование (4.6) дает:
Следовательно, условие постоянства эластичности замещения труда капиталом дает степенную зависимость между величинами MRSLK и k. Соответственно, случай единичной эластичности будет соответствовать линейной связи между указанными величинами:
Введение понятия постоянной эластичности замещения привело к общей форме однородной ПФ, для которой эластичность замещения факторов постоянна. Такие ПФ называют ПФ класса CES (Constant Elasticity of Substitution). Впервые функции этого класса были предложены Эрроу Кеннетом и Солоу Робертом в 1961 году. Функции этого класса предполагают, что замещение труда капиталом возможно только в некоторых пределах и не существует технологий, которые позволяли бы произвести заданное количество продукта при затратах факторов производства ниже определенных критических значений. (Геометрически это означает, что можно построить асимптоты к изокванте, и они будут соответствовать минимально возможным значениями труда и капитала. Возможен вывод математических соотношений асимптот, в данном изложении этот материал мы не будем приводить.) Многие ПФ являются по сути частными или предельными случаями функций CES, основные характеристики которых приведены в Табл 4.1. Табл 4.1
Понятие производственной системы и производственного процесса. Технологический процесс и технологическое множество Основная задача любого производственного процесса - создание добавленной стоимости и нового экономического продукта, который затем участвует в последующих процессах обмена и потребления. Известно, что производственный процесс является условием возникновения процессов потребления с одной стороны, а с другой, прекращение потребления приводит к прекращению производственного процесса. Следовательно, развитие производственных процессов определяется экономическим поведением потребителя. Эту взаимосвязь можно представить в виде следующей концептуальной модели по функционирования экономического объекта: Центральным звеном является модель производственного процесса, которая связывает входные переменные производственной системы с выходными; модель рынка ресурсов является необходимым условием функционирования производственного процесса; модель рынка товаров – необходимое условие существования и возобновления производственного процесса; модель принятия решений – выбор наилучшего в некотором смысле решения товаропроизводителя об объемах выпуска на основе информации о рыночной конъюнктуре и производственных возможностях. Современные представления в области моделирования производственных процессов базируются на теориях экономистов - неоклассиков, которые предложили модель человека «экономического», хозяйственное поведение которого определяется функцией полезности. Таким образом, производственный процесс – это процесс создания добавленной стоимости путем целенаправленного преобразования одного набора товаров в другой. Экономическая система, в которой организован и протекает производственный процесс, называется производственной системой или производством. Цель любой производственной системы – желаемое конкретное конечное будущее состояние или результат хозяйственной деятельности. С точки зрения неоклассической экономической теории целями производителя являются максимизация дохода или прибыли, или минимизация издержек. Потребляемые товары в процессе производства называют производственными факторами, полученные товары в результате производственного процесса – продуктами производства. С этой точки зрения любая производственная система со сложной внутренней структурой представляет собой «черный ящик», при этом известной является информация о производственных факторах (входная информация) и продукте производства (результат), а неизвестная внутренняя структура описывается с помощью некоторой производственной функции. При этом надо помнить о том, что модель «черного ящика» полезна для экономиста, но бесполезна для менеджера, реформирующего организационную структуру и процессы внутри системы. Помимо понятия производственных функций для моделирования производственных процессов важны такие понятия, как концепция эластичности факторов производства, предельной нормы замещения факторов производства, так как ресурсы в производственной системе могут выступать в роли товаров-субститутов. Кроме того, в реальном производственном процессе невозможно производить продукт при полном отсутствии какого-либо фактора производства, то есть можно говорить о взаимодополняемости факторов производства, то есть об их комплементарности. Технология - это технический способ преобразования факторов производства в продукты. Существует огромное число доступных технологий, из которых производители выбирают самые эффективные. Технология задает отношение между элементом u из числа факторов производства и элементом v из области продуктов. Технологический процесс – это совокупность отношений между элементами ui и vj ( 1. невозможность существования «рога изобилия», то есть нулевой технологический процесс (без затрат факторов производства) принадлежит технологическому множеству и означает бездействие; 2. технологическое множество выпукло, то есть технологические процессы можно комбинировать (некоторый технологический процесс может являться выпуклой комбинацией других); 3. технологическое множество ограничено сверху, что связано с ограниченностью (исчерпаемостью) ресурсов (факторов производства); 4. технологическое множество замкнуто, то есть имеет границы. Эффективные технологические процессы описываются точками, лежащими на эффективной границе выпуклого технологического множества. Метод технологических множеств позволяет описать многономенклатурное производство, так как возможен строгий переход от технологических множеств к производственным функциям путем агрегирования факторов производства и продуктов. В заключение отметим, что существует два альтернативных подхода к решению задачи оптимального управления производственными процессами. Первый подход рассматривает задачу максимизации производства продукта при фиксированных бюджетных ограничениях. Решение этой задачи основано на анализе производственной функции производственной системы с учетом рыночной стоимости труда и капитала и размера производственного бюджета. Второй подход решает задачу минимизации производственных издержек при заданном уровне производства продукта. Эта задача решается с использованием функции затрат, которая может быть вычислена по имеющейся производственной функции. Эти два подхода приводят к одинаковому результату при решении оптимизационных задач. (Вспомнить двойственность!).
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.007 с.) |



 , (4.2)
, (4.2) .
. (4.3)
(4.3) - предельная норма замещения капитала трудом;
- предельная норма замещения капитала трудом; - предельная норма замещения труда капиталом.
- предельная норма замещения труда капиталом.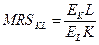
 , где к – фондовооруженность.
, где к – фондовооруженность.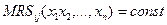
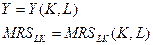

 .
. Например, в точке В значение затрат труда больше, чем в точке А, следовательно, значение MRSLK в точке В меньше, чем в точке А. Соответственно точка В будет соответствовать меньшему значению фондовооруженности, чем в точке А.
Например, в точке В значение затрат труда больше, чем в точке А, следовательно, значение MRSLK в точке В меньше, чем в точке А. Соответственно точка В будет соответствовать меньшему значению фондовооруженности, чем в точке А. (4.4)
(4.4) Графически можно также показать, что с ростом кривизны изокванты эластичность Eσ уменьшается (см. Рис. 4.3).
Графически можно также показать, что с ростом кривизны изокванты эластичность Eσ уменьшается (см. Рис. 4.3).
 (4.5)
(4.5) (4.6)
(4.6) или после преобразования:
или после преобразования: , где
, где 
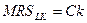
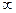

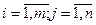 ), поэтому он является простейшей моделью производственного процесса. В свою очередь, совокупность технологических процессов образует технологическое множество. Технологические множества обладают следующими свойствами:
), поэтому он является простейшей моделью производственного процесса. В свою очередь, совокупность технологических процессов образует технологическое множество. Технологические множества обладают следующими свойствами:


