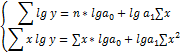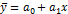Малая выборка: понятие, характеристика, сфера применения. Ошибка малой выборки.

При контроле качества товаров в экономических исследованиях эксперимент может проводиться на основе малой выборки.

Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.
Средняя ошибка малой выборки вычисляется по формуле:
,
где — дисперсия малой выборки.
При определении дисперсии число степеней свободы равно n-1:
.
Предельная ошибка малой выборки определяется по формуле

При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, в которых даны распределения стандартизированных отклонений:
.

 

Основные понятия корреляционного и регрессионного анализа.

Задачи, поставленные перед корреляционным методом исследования, решаются с помощью следующих методов анализа:

1) качественного анализа с отбором взаимосвязанных признаков

2) графического метода

3) определения тесноты связи

 

Этапы проведения корреляционного анализа:

1) определение зависимости между признаками: предполагает качественный анализ в обработке первичного материала, отбор факторов, определение зависимостей определяется с помощью метода группировок

2) выбор формы связи: осуществляется с помощью графического метода с последующим нанесением на график результатов, полученных на основании построенной корреляционно-регрессионной модели

Количественное определение степени влияния факторных признаков на результативный признак. Мерой существенности влияния являются показатели тесноты связи. Это линейный коэффициент корреляции при прямолинейной форме связи, и корреляционное отношение при криволинейной форме связи.

При линейной форме зависимости для измерения тесноты связи, кроме корреляционного отношения используется также коэффициент корреляции, который определяется по формуле:

Коэффициент корреляции может принимать значения [-1;1]. Отрицательные значения указывают на наличие обратной связи, то есть убывающей линейной зависимости. Положительные значения указывают на наличие прямой возрастающей линейной зависимости. Если коэффициент корреляции равен 0, то можно сделать вывод, что линейная связь отсутствует.

При криволинейной зависимости в статистике для характеристики связи используется показатель, представляющий собой долю межгрупповой дисперсии к общей дисперсии. Это эмпирический коэффициент детерминации.

На его основе можно получить эмпирическое корреляционной отношение:

Оно характеризует влияние признака, положенного в основание группировки на вариацию результативного признака (0< <1)

Максимально тесная связь – это связь функциональная, когда каждое значение признака результата У может быть однозначно определено значением Х, при этом остаточная дисперсия равна 0, коэффициент детерминации также равен 0. Таким образом, чем ближе значение показателя к 1, тем сильнее связь между признаками.

 

Наименование функции	Система нормальных уравнений для нахождения параметров уравнения
Линейная
Парабола (2-го порядка)
Показательная
Гиперболическая

Регрессионный метод анализа

По характеру расположения точек в корреляционном поле сделаем вывод о форме связи, то есть, каким уравнением можно выразить тенденцию развития изучаемого процесса. Соединив точку прямыми, получим эмпирическую линию связи, показывающую, что взаимосвязи систематически нарушают влияние прочих факторов. При таком подходе, когда сочетается качественный анализ с применением математических методов, обеспечивается точность полученных результатов и их практическая значимость.

 

Зависимости между признаками выражаются следующими уравнениями:

Линейная
Парабола (2-го порядка)
Показательная
Гиперболическая

 

Нахождение параметров теоретической линии связи равносильно выравниванию эмпирических данных. Наиболее распространенных способ – способ наименьших квадратов. (как для прямолинейной зависимости, так и для криволинейной зависимости). Суть его состоит в том, чтобы удовлетворить следующее требование: сумма квадратов отклонений выровненной линии от точек эмпирической кривой должна быть минимальной. Требование наименьших квадратов приводит к решению систем нормальных уравнений, для нахождения параметров a_i.

 

41. Понятие взаимосвязанных признаков как предмет статистического изучения связи. Зада­чи статистического изучения связи

Важнейшей формой связи является причинная, которая определяет все другие формы связей. Сущность причинности состоит в порождении одного явления другим. Вместе с тем причина сама по себе не определяет следствие, она зависит также от условий, в которых протекает действие причины. Для возникновения следствия нужны все определяющие его факторы – причина и условия.

Необходимая обусловленность явлений множеством факторов называется детерминизмом.

Объектами исследования при статистическом изучении связей служит детерминированность следствия факторами. Признак, характеризующий следствие называется результативным. Признак, характеризующий причины называется факторным.

Задача статистики – это количественная оценка закономерности связи. Математическая определенность позволяет использовать результаты экономических разработок для практических целей.

Существуют различные виды и формы связей, различающиеся по существу, характеру, направлению, тесноте и аналитическому выражению.

1. По характеру зависимости явлений:

1) функциональная, то есть полную связь. При этой связи определенному значению факторного признака во всех случаях соответствует строго определенное значение результативного признака.

2) корреляционную, то есть неполную связь. При этом связи не существует строгого соответствия между значениями взаимосвязанных признаков. В этом случае одному и тому же значению одного признака обычно соответствует ряд значений другого признака. Такие отношения зависимости называются корреляционными.

2. По направлению:

1) прямая связь: связь, при которой с ростом значений факторного признака растут значения результативного признака

2) обратная связь: связь, при которой с увеличением значений величина одного признака, не зависящего от него другого признака, уменьшается

3. По аналитическому выражению

1) линейная связь: связь, которая может быть выражена аналитическим уравнением прямой линии

2) криволинейная связь: связь, выраженная уравнением какой-либо кривой линии (гипербола, парабола)

4. По количеству факторов, то есть факторов, действующих на результативный признак

1) однофакторная связь (парные)

2) многофакторная связь