Лабораторная работа №3. Функции просмотра и ссылок

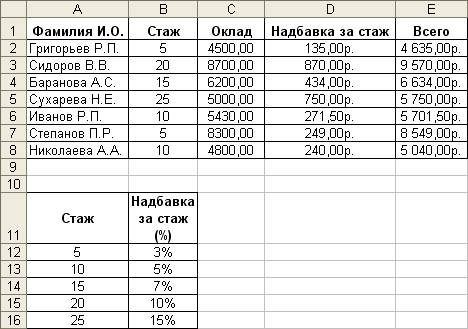
Задание 1. Сформировать ведомость заработной платы, в которой надбавка за стаж определяется исходя из соответствующих надбавок за количество отработанных лет.

Ход работы:

1. Сформируйте ведомость и дополнительную таблицу, как показано на рис. 8.

2. В ячейку D2 введите формулу:

=С2*ВПР(В2;$А$16:$В$20;2),

где:

• В2 — искомое значение (стаж сотрудника), которое необходимо найти в крайнем левом столбце таблицы, определяемой диапазоном $А$12:$В$16;

• индекс 2 определяет номер столбца таблицы, из которого будет возвращено значение (в данном случае, процент надбавки);

• С2 — оклад сотрудника.

функции ВПР() и ГПР() используются для поиска информации в прямоугольных таблицах. Данные функции имеют следующий синтаксис:

=ВПР(искомое_знач; таблица; номер_столбца; тип_просмотра);

=ГПР(искомое_знач; таблица; номер_строки; тип_просмотра),

где:

• искомое_знач— это значение, которое необходимо найти в первом столбце (строке) таблицы;

Рис. 8. Исходные данные для ведомости зарплаты

• таблица— массив или имя диапазона, который определяет таблицу с данными. Первый столбец (строка) должны быть упорядочены в алфавитном порядке текстовых значений или в порядке возрастания числовых данных, а также значений даты/времени;

•номер_столбца (номер_строки) — указывает, из какого столбца (строки) таблицы следует выбирать возвращаемое значение;

• тип_просмотра — определяет логическое значение для указания типа соответствия: точное или приближенное. Если аргумент опущен, то используется приближенное сравнение, что означает поиск наибольшего сравниваемого значения, которое меньше или равно искомому значению.

Поиск осуществляется по следующему правилу: Искомое значение сравнивается с данными, расположенными в крайнем левом столбце для функции ВПРО (ИЛИ В верхней строке для функции ГПРО) таблицы, и таким образом определяется первый индекс возвращаемого значения. Номер столбца (номер строки) задает второй индекс, определяющий строку или столбец таблицы, из которой возвращается значение.

3. В ячейку Е2 введите формулу =C2+D2.

4. Скопируйте формулы в соответствующие диапазоны.

5. Отформатируйте таблицу.

Результат для этого примера представлен на рис. 9.

Рис. 9. Ведомость заработной платы

Лабораторная работа №4. Финансовые функции MS Excel.

 

Финансовые функции MS Excel предназначены для вычисления базовых величин, необходимых при проведении сложных расчетов.

 

Задание 1. Определить величину основного платежа за четвертый год, если выдана ссуда размером 1 000000000 сроком на 5 лет под 12% годовых.

Решение

Для основных платежей по займу, который погашается равными платежами в конце или начале каждого расчетного периода, в MS Excel XP используется функция:

ОСПЛТ (Ставка, Период, Кпер, Пс, Бс)

(в более ранних версиях MS Excel эта функция называлась ОСНПЛАТ) В нашем случае функция СППЛТ имеет вид: ОСПЛТ(12%, 4, 5, 1000000000)

Ввод данных и расчеты производятся в соответствии с рис. 4.4.

Рис. 11. Расчет основных платежей по займу

В ячейку В8 вводится формула:

ОСПЛТ (В5;В6;В4;ВЗ)

Задание 2. Рассчитать 20-летнюю ипотечную ссуду ей ставкой 10% годовых при начальном взносе 25% и ежемесячной (ежегодной) выплате.

Решение

Для вычисления величины постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке используется функция ПЛТ (в ранних версиях — функция ППЛАТ):

ПЛТ(Ставка; Кпер; Бс; Пс; Тип)

В нашем случае функция ПЛТ имеет вид:

ПЛТ(10%/12; 20*12; -(350000* (1-25%)))— ежемесячные выплаты;

ПЛТ(10%; 20; -(350000* (1-25%)))—ежегодные выплаты.

Решение задачи приведено на рис. 12 и 13.

Рис. 12. Расчет ипотечной ссуды

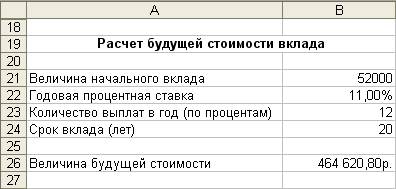
Рис. 13. Формулы для расчета ипотечной суды

Задание 3. Определить, какая сумма окажется на счете, если 52 000 руб. положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.

Решение

Для расчета будущей стоимости единой суммы вклада используются сложные проценты, а расчетная формула основана на функции БС (в ранних версиях — функция БЗ):

БС(Ставка; Кпер; Плт; Пс; Тип)

Для нашей задачи функция БС примет вид:

БС(11%/12;20*12;,-52000)

Решение задачи приведено на рис. 14, а формула для ячейки В26:

=БС(B22/B23;B24*B23;;-B21)

Рис. 14. Расчет будущей стоимости вклада

Задание 4. Облигация номиналом 200 000 руб. выпущена на 7 лет. Предусматривается следующий порядок начисления процентов: в первый год— 11%, последующие три года— по 16%, в оставшиеся

три года— по 20%. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.

Решение

Для расчета наращенной стоимости облигации по сложной процентной ставке используется функция:

БЗРАСПИС(Первичное; План)

Для нашей задачи функция принимает вид:

БЗРАСПИС(200000; {11%; 16%; 16%; 16%; 20%; 20%; 20%))

Решение приведено на рис. 15, а формула для расчета в ячейке В42:

=БЗРАСПИС(В30;В34:В40)

 

Аналогичным образом можно использовать встроенные функции MS Excel и для других финансовых расчетов.

 

Рис. 15 Расчет наращенной стоимости облигации по сложной процентной ставке