
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Логика и язык праваСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Лекция 1. Логика и язык права
1. Понятие и виды языков Язык – это знаковая система, выполняющая функцию формирования, хранения и передачи информации в процессе познания действительности и общения между людьми. Комплексное изучение языка осуществляется общей теорией знаковых систем – семиотикой. По своему происхождению языки бывают естественные и искусственные. Естественные языки – это исторически сложившиеся в обществе звуковые (речь) и графические (письмо) знаковые системы. Они являются носителями многовековой культуры народов. Искусственные языки – это вспомогательные знаковые системы, создаваемые на базе естественных языков для точной и экономной передачи научной и другой информации. Юридический язык или язык права является одним из искусственных языков. Для современной логики общепринятым искусственным языком является язык логики предикатов. Алфавит этого языка включает следующие виды знаков: 1) a, b, c, … - символы для единичных имен предметов (предметные константы); 2) x, y, z, … - символы общих имен предметов (предметные переменные); 3) P, Q, R, … - символы для обозначения свойств предметов или отношений между ними (предикатные переменные); 4) p, q, r, … - символы для обозначения высказываний (пропозициональные переменные); 5) ", $ - символы для количественной характеристики высказываний (кванторы); " - квантор общности, он символизирует выражения: все, каждый, всякий; $ - квантор существования, он символизирует выражения: некоторый, иногда, бывает, встречается, существует и т.п.; 6) логические связки: & - конъюнкция (союз «и»); Ú - дизъюнкция (союз «или»); - импликация (союз «если…, то…»); «- эквиваленция (союз «если и только если…, то…»); ``p – отрицание («неверно, что…»). Допустимые в языке логики предикатов выражения называются правильно построенными формулами (ППФ).
2. Основные логические законы Логический закон – это необходимая существенная связь мыслей в процессе рассуждения. Основными логическими законами являются законы тождества, противоречия, исключенного третьего и достаточного основания. Первые три закона были выявлены и сформулированы древнегреческим философом Аристотелем, а закон достаточного основания – немецким философом Г.В. Лейбницем в XVIII веке. 1. Закон тождества Сущность данного закона заключается в следующем: любая мысль в процессе рассуждения должна быть тождественна самой себе. Обозначается это так: а есть а или а=а, где под а понимается любое понятие или p®p, где p – некоторое высказывание. Нарушение этого закона выражается в отождествлении различных понятий и представляет собой логическую ошибку, называемую подменой понятий. 2. Закон противоречия Два несовместимых друг с другом высказывания не могут быть одновременно истинными, одно из них должно быть ложным. Обозначается это так: неверно, что p и 3. Закон исключенного третьего Два противоречащих высказывания не могут быть одновременно ложными, одно из них должно быть истинным. Обозначается это так: (p или p Ú Согласно последним двум законам, одно из двух противоречащих высказываний должно быть истинным, а другое – ложным, третьего не дано. Закон достаточного основания Всякая мысль признается истинной, если она имеет достаточное основание. «После» не означает «из-за» или «вследствие». Достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и установленная мысль, из которой с необходимостью вытекает истинность данной мысли. p, p®q ———— – правило логического вывода modus ponens q p – основание, которое должно быть достаточным, а q – следствие или вывод.
Лекция 2. Понятия
1. Понятие как форма мышления
Обратить внимание на соотношение понятия и слова (синонимы, омонимы). Понятие – это форма мышления, в которой отражаются существенные и отличительные признаки отдельного предмета или множества однородных предметов. Признаком предмета называется то, в чем предметы сходны друг с другом или чем они отличаются друг от друга. Неточные (молодой человек, лысый человек) и неясные (человек) понятия. Содержание понятия – это совокупность тех признаков, которые присущи всем предметам, обозначаемым данным понятием, и только им. Например, в содержание понятия «стул» входят признаки: «быть предметом мебели, предназначенным для сидения» и «иметь ножки, сидение и спинку». Объем понятия – это совокупность тех предметов, которые обладают признаками, входящими в содержание понятия. Например, в объем понятия «стул» входят все стулья, какие только были, есть и будут существовать в мире. Пример: понятие «преступление» - содержание и объем. Закон обратного отношения между объемом и содержанием понятия гласит следующее: увеличение содержания понятия ведет к образованию понятия с меньшим объемом, и наоборот. Классом (множеством) называется определенная совокупность предметов, имеющих некоторые общие признаки. Например, классы (множества) высших учебных заведений, студентов, преступлений и т.д. Класс (множество) может включать в себя подкласс (подмножество). Например, класс студентов ТРТУ включает в себя подкласс студентов ФЭМП, класс преступлений – подкласс должностных преступлений. Отношение между классом (множеством) и подклассом (подмножеством) выражается при помощи знака включения Ì: AÌB. Например, если A – адвокаты, а B – юристы, то A будет подклассом класса B. Классы (множества) состоят из элементов. Элемент класса (множества) – это предмет, входящий в данный класс (данное множество). Например, элементами множества высших учебных заведений будут МГУ, РГУ, ТРТУ и т.д. Отношение элемента к классу (множеству) выражается при помощи знака принадлежности Î: aÎA. Например, если a - ТРТУ, A – высшие учебные заведения, то a является элементом множества A. Различают универсальный класс, единичный класс и нулевой (пустой) класс. Универсальный класс (универсум) – класс, состоящий из всех элементов исследуемой области. Например, класс планет Солнечной системы. Единичным классом называется класс, состоящий из одного элемента. Например, планета Земля. Нулевым (пустым) классом называется класс, который не содержит ни одного элемента. Например, пустыми классами являются вечный двигатель, круглый квадрат, русалка, леший и др.
2. Виды понятий
Единичные понятия обозначают один и только один предмет. Например, «Москва», «Л.Н. Толстой», «Российская Федерация», «Солнце». Пустое понятие не обозначает ни одного реально существующего предмета. Например, «Зевс», «Пегас», «кентавр», «идеальный газ», «Снегурочка» и т.п. Общие понятия обозначают множество предметов, состоящее из двух и более элементов. Например, «человек», «писатель», «юрист», «студент», «стол», «дом». Общие понятия делятся на регистрирующие и нерегистрирующие. Понятие называется регистрирующим, если множество обозначаемых им предметов поддается учету, регистрируется. Регистрирующие понятия имеют конечный объем. Например, «участник Великой Отечественной войны 1941-1945 гг.», «родственники потерпевшего Петрова», «планета Солнечной системы». Общее понятие, относящееся к неопределенному числу элементов, называется нерегистрирующим. Нерегистрирующие понятия имеют бесконечный объем. Например, «человек», «юрист», «преступление», «закон», «указ», «договор». Конкретными называются понятия, которые обозначают самостоятельно существующие предметы. Абстрактными называются понятия, которые обозначают признак предмета или отношение между предметами. Например, понятия «книга», «свидетель», «государство» являются конкретными, а понятия «белизна», «смелость», «ответственность» – абстрактными. Положительными называются понятия, содержание которых составляют свойства, присущие предмету. Отрицательными называются понятия, в содержании которых указывается на отсутствие у предмета определенных свойств. Например, понятия «грамотный», «порядок», «верующий» являются положительными, а понятия «неграмотный», «беспорядок», «неверующий» являются отрицательными. К отрицательным понятиям также относятся: «невиновный», «невменяемый», «аморальный», «анонимный», «молчаливый», «трезвый» и т.д. Безотносительными называются понятия, которые отражают предметы, существующие раздельно и мыслящиеся вне их отношения к другим предметам. Например, «студент», «государство», «место преступления», «следователь». Соотносительные понятия содержат признаки, указывающие на отношение одного понятия к другому понятию. Например, «родители» (по отношению к понятию «дети»), «начальник» («подчиненный»), «получение взятки» («дача взятки»), «брат», «сосед».
3. Отношения между понятиями Следует различать сравнимые и несравнимые понятия. Сравнимыми называются понятия, которые имеют некоторые признаки, позволяющие сравнивать эти понятия друг с другом. Несравнимыми называются понятия, не имеющие общих признаков, поэтому сравнивать эти понятия невозможно. Например, «пресса» и «телевидение» – сравнимые понятия, т.к. они имеют общие признаки, характеризующие средства массовой информации, а «государство» и «симфоническая музыка» – несравнимые понятия. В логических отношения могут находиться только сравнимые понятия. Сравнимые понятия делятся на совместимые и несовместимые.
Понятия, объемы которых полностью или частично совпадают, называются совместимыми. Существует три вида отношений совместимости: 1. Равнозначность. Равнозначными являются два понятия, объемы которых полностью совпадают (хотя содержание их различно). Например, равнозначными являются понятия: «геометрическая фигура с тремя равными углами» и «геометрическая фигура с тремя равными сторонами», т.к. они обозначают один предмет – правильный (равносторонний) треугольник. 2. Пересечение. В отношении пересечения находятся два понятия, объемы которых частично совпадают. Например, «летчик» и «космонавт». 3. Подчинение. В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, составляя его часть. Например, «преступление» (A) и «должностное преступление» (B). Понятие, имеющее больший объем и включающее объем другого понятия (A), называется подчиняющим, а понятие, имеющее меньший объем (B), называется подчиненным. Если в отношении подчинения находятся два общих понятия, то подчиняющее понятие называется родом, а подчиненное – видом. Например, понятие «должностное преступление» будет видом по отношению к понятию «преступление». В то же время, оно будет родом по отношению к понятию «получение взятки». Если в отношении подчинения находятся общее и единичное понятия, то общее (подчиняющее) понятие называется видом, а единичное (подчиненное) – индивидом. Например, общее понятие «адвокат» является видом, а единичное понятие «М. Барщевский» является индивидом. Несовместимыми называются понятия, объемы которых не совпадают ни полностью, ни частично. Существует три вида отношений несовместимости: 1. Соподчинение. В отношении соподчинения находятся два непересекающихся понятия, подчиненных общему для них понятию. Например, соподчиненными являются понятия «адвокат» и «следователь», а общим для них является понятие «юрист». 2. Противоположность. Противоположными называются понятия, которые составляют в сумме только часть объема общего для них родового понятия, видами которого они являются, и которому они соподчинены. Например, «черный» и «белый», «отличник» и «двоечник», «дружественное государство» и «враждебное государство». 3. Противоречие. Противоречащими называются понятия, объемы которых в сумме составляют весь объем рода, видами которого они являются, и которому они соподчинены. Например, «черный» и «нечерный», «виновный» и «невиновный», «дружественное государство» и «недружественное государство».
Операции с классами В операциях с классами приняты следующие обозначения: A, B, C и т.д. – произвольные классы, E - универсальный класс (универсум), Æ - нулевой (пустой) класс. 1. Операция объединения (сложения) классов состоит в объединении двух или нескольких классов в один класс, состоящий из элементов – слагаемых классов. Операция объединения обозначается знаком È: C=AÈB. Например, если A – множество всех инструкций Минфина РФ, B – множество всех инструкций Минэкономики РФ, то C=AÈB – множество всех инструкций Минфина РФ или Минэкономики РФ. 2. Операция пересечения (умножения) классов состоит в отыскании элементов, общих для двух или нескольких классов. Операция пересечения обозначается знаком Ç: D=AÇB. Например, при пересечении классов инструкций Минфина РФ и Минэкономики РФ образуется класс инструкций, принятых одновременно двумя органами: и Минфином РФ, и Минэкономики РФ. При пересечении множеств, входящих в несовместимые понятия, получается нулевой (пустой) класс, так как элементов, входящих одновременно в оба понятия, не существует. Например, если А – множество законов, а В – множество постановлений, то AÇB=Æ. Операцию пересечения (умножения) можно выполнять не только для двух, но и для большего количества классов. Например, D=AÇBÇC, где А – юристы, В – депутаты, С – москвичи, D – юристы, являющиеся депутатами и москвичами. 3. Образование дополнения (отрицание) – это операция по образованию нового класса путем исключения данного класса (A) из универсального класса (E), к которому оно принадлежит (AÌE). Полученный в результате класс называется отрицанием исходного класса и обозначается Например, исключая множество адвокатов (A) из универсального класса юристов (E), образуем отрицание
Лекция 4. Суждение и норма
1. Суждение как форма мышления Суждение – это форма мышления, в которой утверждается или отрицается связь или отношение между понятиями и которая может быть либо истинной, либо ложной. Суждение выражается повествовательным предложением, в котором содержится сообщение о чем-либо. Истинность суждения определяется его соответствием объективной действительности. Истинные – это такие суждения, в которых связь понятий правильно отражает реальные свойства и объективную действительность. Ложные – это такие суждения, в которых связь понятий искажает объективную действительность. Истинные суждения обозначаются следующим образом: «Истинно», И, 1, а ложные – «Ложно», Л, 0. Истинность или ложность суждения называется значением его истинности. Суждения делятся на простые и сложные.
2. Простые суждения Простым называется суждение, которое выражает связь двух понятий. Простые суждения, в свою очередь, делятся на: 1) атрибутивные (категорические) – это суждения о признаке предмета. Они состоят из субъекта (S), предиката (P) и связки (логическая схема S – P). Субъектом называется понятие о предмете суждения. Предикатом называется понятие о признаке предмета. Связка выражает отношение между субъектом и предикатом. Субъект и предикат называются терминами суждения. Примеры: «Россия (S) – суверенное государство (P)». «Никто из судей (S) не вправе воздержаться от голосования (P)». Объемная интерпретация – круговые схемы. 2) суждения с отношением – суждения, отражающие отношение между предметами. Это могут быть отношения равенства, неравенства, родства, пространственные, временные, причинно-следственные и другие. Логическая структура: xRy, где x и y – члены отношения, они обозначают понятия о предметах, R – отношение между ними. Примеры: A равно В; С больше D; Семен – отец Сергея; Казань восточнее Москвы; Мораль возникла раньше права. 3) суждения существования (экзистенциальные) выражают сам факт существования или несуществования предмета суждения. Примеры: Существуют логические законы; На Земле уже нет многих видов животных. Атрибутивные (категорические) суждения делятся по качеству на утвердительные, выражающие принадлежность предмету некоторого признака (S есть P), и отрицательные, выражающие отсутствие у предмета некоторого признака (S не есть P). Примеры: Обвиняемый не обязан доказывать свою невиновность; Данное лицо признано невменяемым. Они также делятся по количеству на единичные, частные и общие, в которых что-либо утверждается или отрицается соответственно об одном предмете, о некоторых или обо всех предметах. Частные суждения, в свою очередь, делятся на определенные и неопределенные. В неопределенном частном суждении слово «некоторые» употребляется в значении «некоторые, а может быть, и все»: Некоторые свидетели дали показания. В определенном частном суждении слово «некоторые» употребляется в значении «только некоторые»: Лишь некоторые свидетели дали показания.
По объединенной классификации по количеству и качеству суждения делятся на: А – общеутвердительные (все S есть P); Е – общеотрицательные (ни одно S не есть P); I – частноутвердительные (некоторые S есть P); О – частноотрицательные (некоторые S не есть P). M есть P S есть М S есть P
Общие правила категорического силлогизма: а) правила терминов: 1. В силлогизме должно быть только три термина. 2. Средний термин должен быть распределен хотя бы в одной из посылок. 3. Термин, не распределенный в посылке, не может быть распределен и в заключении. б) правила посылок: 1. Хотя бы одна из посылок должна быть утвердительным суждением. 2. Если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным. 3. Хотя бы одна из посылок должна быть общим суждением. 4. Если одна из посылок — частное суждение, то и заключение должно быть частным. Фигуры и модусы категорического силлогизма. Фигуры силлогизма – это его разновидности, различающиеся положением среднего термина в посылках. Существует 4 вида фигур:
Посылками силлогизма могут быть суждения, различные по качеству и количеству: АА ЕА IА ОА АЕ (ЕЕ) IЕ (ОЕ) АI ЕI (II) (ОI) АО (ЕО) (IО) (ОО) Разновидности силлогизма, различающиеся количеством и качеством посылок, называются модусами простого категорического силлогизма. Если отобрать только те модусы, которые согласуются с общими правилами силлогизма, то получим 19 модусов, которые называются правильными. Их записывают вместе с заключениями: 1-я фигура: ААА, ЕАЕ, АII, ЕIО 2-я фигура: ЕАЕ, АЕЕ, ЕIО, АОО 3-я фигура: ААI, IАI, АII, ЕАО, ОАО, ЕIО 4-я фигура: ААI, АЕЕ, IАI, ЕАО, ЕIО Особые правила фигур силлогизма. Каждая фигура имеет свои особые правила, которые выводятся из общих. Правила 1-й фигуры: 1. Большая посылка – общее суждение. 2. Меньшая посылка – утвердительное суждение. Правила 2-й фигуры: 1. Большая посылка – общее суждение. 2. Одна из посылок – отрицательное суждение. Правила 3-й фигуры: 1. Меньшая посылка – утвердительное суждение. 2. Заключение – частное суждение. Иван – брат Сергея Петр – брат Сергея
Логическим основанием таких умозаключений являются свойства отношений 1) Симметричность: xRy ® yRx
xRy А похож на В _______ ____________ yRx В похож на А
2) Рефлексивность: xRy ® (xRx & yRy)
xRy a=b _________ __________ xRx & yRy a=a и b=b
3) Транзитивность: (xRy & yRz) ® xRz
xRy Петр – брат Ивана yRz Иван – брат Сергея ______ _________________ xRz Петр – брат Сергея
2. Дедуктивные выводы из сложных суждений Дедуктивными выводами из сложных суждений называются дедуктивные умозаключения, в которых одна из посылок представляет собой сложное суждение. К ним относятся: чисто условное, условно-категорическое, разделительно-категорическое и условно-разделительное умозаключения. 1. Чисто условное умозаключение Чисто условным называется умозаключение, обе посылки которого являются условными суждениями. Схема чисто условного умозаключения: Если p, то q В символической записи: Если q, то r (p®q)&(q®r) ——————— ——————————— Если p, то r p®r Пример. Если понятые не приглашены, то процессуальный порядок обыска нарушен. Если нарушен процессуальный порядок обыска, то найденные при обыске предметы не могут считаться доказательствами. —————————————————————————————————— Если понятые не приглашены, то найденные при обыске предметы не могут считаться доказательствами. 2. Условно-категорическое умозаключение Условно-категорическим называется умозаключение, в котором одна из посылок – условное суждение, а другая посылка и заключение – простое категорическое суждение. Данный вид умозаключения имеет две разновидности: 1) утверждающий модус (modus ponens), в котором рассуждение направлено от утверждения основания к утверждению следствия; 2) отрицающий модус (modus tollens), в котором рассуждение направлено от отрицания следствия к отрицанию основания. Схема утверждающего модуса (modus ponens): Если p, то q В символической записи: p (p®q), p ——————— ————— q q Пример. Если состав преступления отсутствует (p), то уголовное дело не может быть возбуждено (q). Состав преступления отсутствует (p). ——————————————————————— Уголовное дело не может быть возбуждено (q).
Схема отрицающего модуса (modus tollens): Если p, то q В символической записи: не-q (p®q), ——————— ————— не-p Пример. Если иск предъявлен недееспособным лицом (p), то суд оставляет иск без рассмотрения (q). Суд не оставил иск без рассмотрения ( —————————————————————— Иск предъявлен дееспособным лицом ( Обратная дедукция. Кроме рассмотренных выше, существуют также еще умозаключения, которые строятся по схемам обратной дедукции. Все эти схемы дают вероятностные заключения, которые ни в коем случае нельзя считать достоверными или доказанными.
1. Схема, обратная правилу modus ponens: Если p, то q В символической записи: q (p®q), q ——————— ————— вероятно, p вероятно, p Пример. Если Петров совершил это преступление (p), то он знал потерпевшего (q). Петров знал потерпевшего (q). ——————————————————————— Вероятно, Петров совершил это преступление (p).
2. Схема, обратная правилу modus tollens: Если p, то q В символической записи: не-p (p®q), ——————— ————— вероятно, не-q вероятно, Пример. Если у Петрова есть алиби (p), то преступление совершил не он (q). У Петрова отсутствует алиби ( —————————————————————— Вероятно, преступление совершил Петров (
3. Разделительно-категорическое умозаключение Разделительно-категорическим называется умозаключение, в котором одна из посылок – разделительное, а другая посылка и заключение – простые категорические суждения. Этот тип умозаключения делится на два вида: 1) утверждающе-отрицающий модус (modus ponendo tollens), в котором вторая посылка (категорическое суждение) утверждает один из членов дизъюнкции, а заключение отрицает другой ее член; 2) отрицающе-утверждающий модус (modus tollendo ponens), в котором вторая посылка отрицает один дизъюнкт, а заключение утверждает другой. Схема утверждающе-отрицающего модуса: p или q В символической записи:
——————— ————— не-q Обратим внимание на то, что между p и q в этой схеме – строгая дизъюнкция (либо, либо)! Пример. Облигации могут быть предъявительскими (p) или именными (q) Данная облигация предъявительская (p) ————————————————————————————— Данная облигация не является именной ( Схема отрицающе-утверждающего модуса: p или q В символической записи: не-p <p Ú q>, ——————— ————— q q где <…> - обозначает полную или закрытую дизъюнкцию
Пример. Облигации могут быть предъявительскими (p) или именными (q) Данная облигация не является предъявительской ( ————————————————————————————— Данная облигация – именная (p) 4. Условно-разделительное умозаключение Умозаключение, в котором одна посылка – условное, а другая – разделительное суждение, называется условно-разделительным или лемматическим (от латинского lemma – предположение). Разделительное суждение может содержать две, три и большее число альтернатив. Поэтому лемматические умозаключения делятся на дилеммы (две альтернативы), трилеммы (три альтернативы) и т.д. Различают два вида дилемм: конструктивную и деструктивную, каждая из которых делится на простую и сложную. 1) Схема простой конструктивной дилеммы: Если p, то r; если q, то r В символической записи: p или q (p®r)&(q®r), p Ú q ——————————— ——————————— r r В простой конструктивной дилемме условная посылка содержит два основания, из которых вытекает одно и то же следствие. Разделительная посылка утверждает оба возможных основания, а заключение утверждает следствие. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствия. Пример. Если обвиняемый виновен в заведомо незаконном аресте (p), то он подлежит уголовной ответственности (r); если он виновен в заведомо незаконном задержании (q), то он также подлежит уголовной ответственности (r). Обвиняемый виновен или в заведомо незаконном аресте (p), или в заведомо незаконном задержании (q). ——————————————————————————— Обвиняемый подлежит уголовной ответственности (r).
2) Схема сложной конструктивной дилеммы: Если p, то q; если r, то s В символической записи: p или r (p®q)&(r®s), p Ú r ——————————— ——————————— q или s q Ú s В сложной конструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка утверждает оба возможных основания. Рассуждение направлено от утверждения истинности двух оснований к утверждению истинности двух следствий. Пример. Если облигация является предъявительской (p), то она передается другому лицу путем вручения (q); если она является именной (r), то передается в порядке, установленном для уступки требований (s). Облигация может быть предъявительской (p) или именной (r). —————————————————————————————— Облигация передается другому лицу путем вручения (q) или в порядке, установленном для уступки требований (s).
3) Схема простой деструктивной дилеммы: Если p, то q; если p, то r В символической записи: не-q или не-r (p®q)&(p®r), ——————————— ——————————— не-p В простой деструктивной дилемме условная посылка содержит одно основание, из которого вытекает два возможных следствия. Разделительная посылка отрицает оба следствия, а заключение отрицает основание. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности основания. Пример. Если Н – подозреваемый (p), значит, он или задержан по подозрению в совершении преступления (q), или является лицом, к которому применена мера пресечения до предъявления обвинения (r). Н не был задержан по подозрению в совершении преступления ( или он не является лицом, к которому применена мера пресечения до предъявления обвинения ( —————————————————————————————————————— Н не является подозреваемым ( 4) Схема сложной деструктивной дилеммы: Если p, то q; если r, то s В символической записи: не-q или не-s (p®q)&(r®s), ——————————— ——————————— не-p или не-r В сложной деструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка отрицает оба следствия, заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований. Пример. Если административное правонарушение совершено военнослужащим (p), то он несет ответственность в соответствии с дисциплинарным уставом (q); если оно совершено дипломатом (r), то вопрос о его ответственности разрешается в соответствии с нормами международного права (s). Правонарушитель привлекался к ответственности не на основании дисциплинарного устава ( или не в соответствии с нормами международного права ( —————————————————————————————————————— Административное правонарушение совершено не военнослужащим ( или не дипломатом ( 5. Сокращенный силлогизм (энтимема) Силлогизм с пропущенной посылкой или заключением называется сокращенным силлогизмом или энтимемой (в переводе с греческого «энтимема» означает «в уме»). Наиболее распространенными видами энтимем являются: 1. Простой категорический силлогизм с пропущенной первой посылкой. Пример: «Николаев – студент, поэтому он обязан сдавать экзамены». Все студенты обязаны сдавать экзамены – пропущена! Николаев – студент —————————————————— Николаев обязан сдавать экзамены 2. Условно-категорический силлогизм с пропущенной первой посылкой. Пример: «Уголовное дело не может быть возбуждено, т.к. событие преступления не имело места». Если событие преступления не имело места, то уголовное дело не может быть возбуждено - пропущена! Событие преступления не имело места —————————————————————————————————— Уголовное дело не может быть возбуждено 3. Разделительно-категорический силлогизм с опущенной первой посылкой. Пример: «По данному делу не может быть вынесен оправдательный приговор, он должен быть обвинительным». По данному делу может быть вынесен либо оправдательный, либо обвинительный приговор - пропущена! По данному делу не может быть вынесен оправдательный приговор —————————————————————————————————— Приговор должен быть обвинительным 4. Разделительно-категорический силлогизм с опущенным заключением. Пример: «Сделки бывают односторонние, двусторонние и многосторонние. Эта сделка является двусторонней». Заключение, отрицающее все другие альтернативы, обычно не формулируется.
Индуктивные умозаключения Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или элементам некоторого класса делают вывод о его принадлежности классу в целом. Схема индуктивного умозаключения:
Посылки: 1)S1 имеет признак P S2 имеет признак P · · · · · · · · · Sn имеет признак P 2)S1, S2, …, Sn – элементы класса K ——————————————————— Заключение: Всем предметам класса K присущ признак P
Индукция делится на полную и неполную. Полная индукция – это умозаключение, в котором на основе принадлежности каждому элементу класса определенного признака делают вывод о его принадлежности классу в целом. Например, для доказательства причастности к совершению преступления организованной группы необходимо сначала доказать причастность каждого участника группы в отдельности. Однако на практике полная индукция применима лишь в тех случаях, когда имеют дело с закрытыми классами, число элементов в которых является конечным и легко обозримым. При этом выводы, получаемые в результате применения полной индукции, носят доказательный характер и являются достаточно обоснованными или достоверными. Поэтому полную индукцию по сути приравнивают к дедуктивным рассуждениям. Неполная индукция – это умозаключение, в котором на основе принадлежности признака некоторым элементам класса делают вывод о его принадлежности классу в целом. Схема неполной индукции:
Посылки: 1)S1 имеет признак P S2 имеет признак P · · · · · · · · · Sm имеет признак P 2)S1, S2, …, Sm, …, Sn – элементы класса K ——————————————————— Заключение: Вероятно, классу K присущ признак P
Так как в неполной индукции исследуют не все, а лишь некоторые элементы класса K, получаемые в результате в
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 646; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

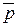 одновременно истинны, где p – любое высказывание; p &
одновременно истинны, где p – любое высказывание; p & 
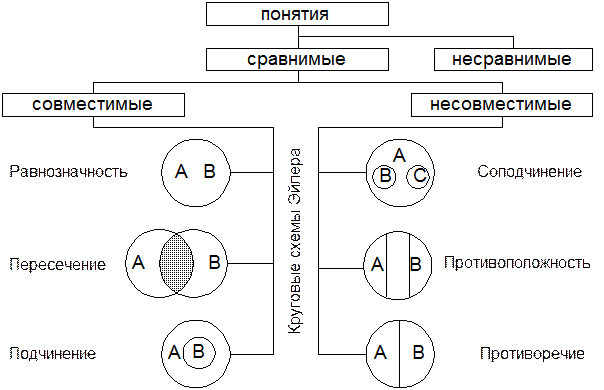
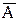 . При этом объединение исходного класса и его отрицания образует универсальный класс: AÈ
. При этом объединение исходного класса и его отрицания образует универсальный класс: AÈ 
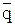
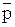
 ).
).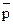 ).
).
 p p Ú q, p
p p Ú q, p
 ).
).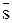
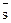 ).
).


