Развитие представлений о пространстве и времени

 

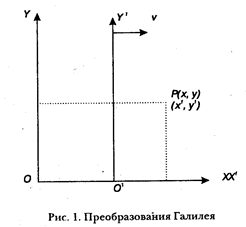
Во второй половине XIX в. физики все чаще анализируют фундаментальные основания классической механики. Прежде всего это касается понятий пространства и времени, их ньютоновской трактовки. Предпринимаются попытки придать понятию абсолютного пространства и абсолютной системы отсчета новое содержание взамен старого, которое им придал еще Ньютон. Так, в 70-е гг. XIX в. было введено понятие α -тела как такого тела во Вселенной, которое можно считать неподвижным и принять за начало абсолютной системы отсчета. Некоторые физики предлагали принять за α-тело центр тяжести всех тел во Вселенной, полагая, что этот центр тяжести можно считать находящимся в абсолютном покое.

Вместе с тем рядом физиков высказывалось и противоположное мнение, что само понятие абсолютного прямолинейного и равномерного движения как движения относительно некоего абсолютного пространства лишено всякого научного содержания, как и понятие абсолютной системы отсчета. Вместо понятия абсолютной системы отсчета они предлагали более общее понятие инерциальной системы отсчета (координат), не связанное с понятием абсолютного пространства. Из этого следовало, что понятие абсолютной системы координат также становится бессодержательным. Иначе говоря, все системы, связанные со свободными телами, не находящимися под влиянием каких-либо других тел, равноправны.

Инерциальные системы - это системы, которые движутся прямолинейно и равномерно относительно друг друга. Переход от одной инерциальной системы к другой осуществляется в соответствии с преобразованиями Галилея. Именно преобразования Галилея характеризуют в классической механике закономерности перехода от одной системы отсчета к другой.

Если система отсчета X'0'Y' (рис. 1) движется прямолинейно и равномерно со скоростью v относительно системы отсчета ХОУ в течение времени t, то 00' = vt, а координаты точки Р в этих системах отсчета связаны между собой следующими соотношениями:

X¹ = Х- vt, Y¹=Y, t¹ = t.

 

 

Преобразования Галилея в течение столетий считались само собой разумеющимися и не нуждающимися в обосновании. Но время показало, что это не так.

В конце XIX в. с резкой критикой ньютоновского представления об абсолютном пространстве выступил немецкий физик и философ Э. Мах. В основе представлений Маха лежало убеждение в том, что «движение может быть равномерным относительно другого движения. Вопрос, равномерно ли движение само по себе, не имеет никакого смысла» *. Это представление Мах переносит не только на скорость, но и на ускорение. В ньютоновской механике ускорение (в отличие от скорости) рассматривалось как абсолютная величина: для того чтобы судить об ускорении, достаточно самого тела, испытывающего ускорение. Иначе говоря, ускорение — величина абсолютная и может рассматриваться относительно абсолютного пространства, а не относительно других тел **. Этот вывод и оспаривал Мах.

* Мах Э. Механика. Историко-критический очерк ее развития. СПб.,1909. С. 187. В связи с этим Мах рассматривал системы Птолемея и Коперника как равноправные, считая последнюю более предпочтительной из-за простоты.

** Ньютон аргументировал это положение примером с вращающимся ведром, в которое налита вода. Этот опыт показывал, что движение воды относительно ведра не вызывает центробежных сил и можно говорить о его вращении самом по себе, безотносительно к другим телам, т.е. остается лишь отношение к абсолютному пространству.

 

С точки зрения Маха, всякое движение относительно пространства не имеет никакого смысла, о движении можно говорить только по отношению к телам, а значит, все величины, определяющие состояние движения, являются относительными. Следовательно, и ускорение тоже относительная величина. К тому же опыт не может дать сведений об абсолютном пространстве. Он обвинил Ньютона в отступлении от принципа, согласно которому в теорию должны вводиться только величины, непосредственно выводимые из опыта.

Правда, Мах слишком широко трактовал отношение естествознания и философии. И от критики недостатков классической механики, от непризнания абсолютного пространства Ньютона он вообще перешел к непризнанию объективного существования пространства, рассматривая его как «хорошо упорядоченные системы рядов ощущений».

Однако, несмотря на субъективно-идеалистический подход к проблеме относительности движения, в соображениях Маха были интересные идеи, которые способствовали появлению общей теории относительности. Речь идет о так называемом принципе Маха, согласно которому инерциальные силы следует рассматривать как действие общей массы Вселенной. Этот принцип впоследствии оказал значительное влияние на А. Эйнштейна. Рациональное зерно принципа Маха состояло в том, что свойства пространства-времени обусловлены гравитирующей материей. Но Мах не знал, в какой конкретной форме выражается эта обусловленность.

К новым идеям о природе пространства и времени подталкивали физиков и результаты математических исследований, открытие неевклидовых геометрий. Так, согласно идее английского математика В. Клиффорда, высказанной в 70-х гг., многие физические законы могут быть объяснены тем, что отдельные области пространства подчиняются неевклидовой геометрии. Более того, он считал, что кривизна пространства может изменяться со временем, а физику можно представить как некоторую геометрию. Клиффорд предложил нечто вроде полевой теории материи, в которой материальные частицы представляют собой сильно искривленные области пространства, а «изменение кривизны пространства и есть то, что реально происходит в явлении, которое мы называем движением материи, будь она весомая или эфирная» *. Вследствие искривления пространства действительная геометрия мира подобна «холмам» на ровной местности, а перемещение частиц материи есть не что иное, как перемещение «холма» от одной точки к другой. Клиффорд принадлежит к ряду немногочисленных в XIX в. провозвестников эйнштейновской теории гравитации.

* Клиффорд В. О пространственной теории материи // Альберт Эйнштейн и теория гравитации. М., 1979. С. 36.