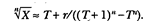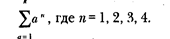Естественно-научные достижения средневековой арабской культуры

 

По-разному сложились исторические судьбы Западной и Восточной Римской империи. Социально-экономический и культурный уровень стран Восточного Средиземноморья, Ближнего Востока (большее их число входило в состав Византийской империи) в эпоху раннего средневековья (вплоть до второй половины XII в.) был выше, чем стран Европы. В VII в. на обширных территориях Ближнего и Среднего Востока возникает централизованное арабское государство — Арабский Халифат. Формирование из ранее разрозненных областей единой политической системы на новой феодальной основе и быстрый рост экономики создали благоприятные условия для развития на средневековом Востоке науки и культуры.

Объединенные политически и экономически, связанные единством религии и языка (арабский язык стал не только государственным, но и языком науки и культуры), народы Ближнего и Среднего Востока получили возможность более свободного обмена духовными ценностями. Благодаря интенсивной переводческой деятельности уже в IX в. в арабоязычном мире были изданы все главные произведения научной мысли античности. К античному наследию арабы относились с величайшим уважением. Так, в 823 г. халиф аль-Мамун потребовал от побежденного им византийского царя Михаила II передать ряд греческих рукописей или их копии. В их числе был получен и «Альмагест» К. Птолемея. Усвоение сложного комплекса местных культурных традиций и культурного наследия античности обеспечило расцвет мусульманской культуры.

Особенно большое распространение на Востоке получили произведения Аристотеля. Вершиной арабоязычного аристотелизма стало творчество Ибн-Рушда (в Европе его называли Аверроэсом), интерпретировавшего труды Аристотеля в духе материализма и пантеизма. Ибн-Рушд развивал и учение о вечности материального мира, являющегося, однако, как учил Аристотель, конечным в пространстве. Ибн-Рушд стремился утвердить полную независимость философии и науки от теологии, мусульманского богословия, минимизировать функции бога по отношению к миру, считая, что бог влияет только на общий ход мирового процесса, но не на его частности. В учении Ибн-Рушда природа максимально независима от бога и сама может творить свои частные, конечные формы. Подобное ограничение креационизма создавало мировоззренческую основу для утверждения идеалов естественно-научного познания.

Ибн-Рушд разработал также «теорию двух истин» — научно-философской и теологической. Как наука (философия), так и религия (теология) размышляют прежде всего о Боге — первой и высшей причине всего существующего и познаваемого. Но они совершенно различны по способу своих разъяснений. Более совершенный способ дает наука (и философия), опирающаяся на логику и доказательства. Религия (и теология) дает образное, чувственное познание, представление Бога, содержащее множество логических противоречий. В Коране можно найти два смысла — буквальный и «внутренний»: первый постигается богословием, второй — наукой, философией. Теория «двух истин» способствовала утверждению философских предпосылок естественно-научного познания.

 

Математические достижения

 

Арабы существенно расширили античную систему математических знаний. Они заимствовали из Индии и широко использовали десятичную позиционную систему счисления. Она проникла по караванным путям на Ближний Восток в эпоху Сасанидов (224—641), когда Персия, Египет и Индия переживали период культурного взаимодействия. И уже из арифметического трактата аль-Хорезми «Об индийских числах», переведенного в XII в. на латынь, десятичная система стала известна в Европе.

Получила также значительное развитие (свойственная еще Древнему Востоку) традиция создания новых вычислительных приемов и специальных алгоритмов. Так, например, аль-Каши с помощью вписанных и описанных правильных многоугольников вычислил число π до 17 верных знаков.

Развивались методы приближенного извлечения корней. Например, такой известный в древности прием:

где Т— целое, был распространен на случай любого натурального показателя корня:

Известен им был и метод вычисления корней, который ныне называется методом Руффини — Горнера*: если

тo последовательное вычисление знаков корня связано с отысканием разностей

* См.: Рыбников К.А. История математики. М., 1974. С. 99.

 

Арабские математики умели также суммировать арифметические и геометрические прогрессии, включая нахождение сумм вида:

Не ограничиваясь методами геометрической алгебры, арабские математики смело переходят к операциям над алгебраическими иррациональностями. Они создали единую концепцию действительных чисел путем объединения рациональных чисел и отношений и постепенно стерли грань между рациональными числами и иррациональными. В Европе эту идею восприняли лишь в XVI в.

Арабские математики совершенствовали методы решения уравнений 2-й и 3-й степеней; решали отдельные типы уравнений 4-й степени. В трактате аль-Хорезми «Книга об операциях джебр (восстановление) и кабала (приведение)», по которому европейские ученые в XII в. начали знакомиться с алгеброй, содержались систематические решения уравнений 1-й и 2-й степени следующих типов:

Наиболее значительным достижением арабов в алгебре был «Трактат о доказательствах задач» Омара Хайяма, посвященный в основном кубическим уравнениям. Хайям построил теорию кубических уравнений, основанную на геометрических методах древних. Он классифицировал все кубические уравнения с положительными корнями на 14 видов; каждый вид уравнений он решал соответствующим построением. Хайям пытался найти правило решения кубических уравнений в общем виде, но безуспешно.

Если отдельные зачаточные элементы сферической тригонометрии были известны еще древним грекам (например, Птолемей пользовался понятием «хорда угла»), то в систематическом виде тригонометрия создана арабскими математиками. Уже в работах аль-Баттани содержится значительная часть тригонометрии, включая таблицы значений котангенса для каждого градуса.

Историческая заслуга средневековых арабских математиков состояла и в том, что они начали глубокие исследования по основаниям геометрии. Так, в сочинениях О. Хайяма и Насирэддина ат-Туси предприняты попытки доказать постулат о параллельных, основанные на введении эквивалентных этому постулату допущений (сумма внутренние углов треугольника равна двум прямым и др.).

 

Физика и астрономия

 

Из разделов механики наибольшее развитие получила статика, чему способствовали условия экономической жизни средневекового Востока. Интенсивное денежное обращение и торговля, как внутренняя, так и международная, требовали постоянного совершенствования методов взвешивания, а также системы мер и весов. Это определило развитие учения о взвешивании и теоретической основы взвешивания — науки о равновесии, создание многочисленных конструкций различных видов весов. Необходимость совершенствования техники перемещения грузов и ирригационной техники в свою очередь способствовала развитию науки о «простых машинах», конструированию устройств для нужд ирригации.

Арабские ученые широко использовали понятие удельного веса, совершенствуя методы определения удельных весов различных металлов и минералов. Этим вопросом занимались аль-Бируни, О. Хайям, аль-Хазини (XII в.). Для определения удельного веса применялся закон Архимеда, грузы взвешивались не только в воздухе, но и воде. Полученные результаты были исключительно точны. Например, удельный вес ртути был определен аль-Хазини в 13,56 г/см3 (по современным данным —13,557); удельный вес серебра 10,30 г/см3 (по современным данным — 10,49), золота — 19,05 г/см3 (современные данные — 19,27), меди 8,86 г/см3 (современные данные — 8,94) и т.д. Столь точные данные позволяли решать ряд практических задач: отличать чистый металл и драгоценные камни от подделок, устанавливать истинную ценность монет, обнаружить различие удельного веса воды при разных температурах и др.

Динамика развивалась на основе комментирования и осмысления сочинений Аристотеля. Средневековыми арабскими учеными обсуждались проблема существования пустоты и возможности движения в пустоте, характер движения в сопротивляющейся среде, механизм передачи движения, свободное падение тел, движение тел, брошенных под углом к горизонту. В работах Ибн-Сины, известного в Европе под именем Авиценна, аль-Багдади и аль-Битруджи, по сути, была сформулирована «теория импетуса», которая в средневековой Европе сыграла большую роль в качестве предпосылки возникновения принципа инерции.

Развитие кинематики было связано с потребностями астрономии в строгих методах для описания движения небесных тел. В этом направлении и развивается аппарат кинематико-геометрического моделирования движения небесных тел на основе «Альмагеста» К. Птолемея. Кроме того, в ряде работ изучалась кинематика «земных» движений. В частности, понятие движения привлекается для непосредственного доказательства геометрических предложений (Ибн Корра Сабит, Насирэддин ат-Туси), механические движения используются для объяснения оптических явлений (Ибн аль-Хайсам), изучается параллелограмм движений и т.п. Одно из направлений средневековой арабской кинематики — разработки инфинитезимальных методов (т.е. рассмотрение бесконечных процессов, непрерывности, предельных переходов и др.).

Существенный вклад внесен арабскими учеными и в астрономию. Они усовершенствовали технику астрономических измерений, значительно дополнили и уточнили данные о движении небесных тел. Один из выдающихся астрономов-наблюдателей аз-Зеркали (Арзахель) из Кордовы, которого считали лучшим наблюдателем XI в., составил так называемые Толедские планетные таблицы (1080); они оказали значительное влияние на развитие тригонометрии в Западной Европе.

Вершиной в области наблюдательной астрономии стала деятельность Улугбека, который был любимым внуком создателя огромной империи Тимура. Движимый страстью к науке, Улугбек построил в Самарканде по тем временам самую большую в мире астрономическую обсерваторию, имевшую гигантский двойной квадрант и много других астрономических инструментов (азимутальный круг, астролябии, трикветры, армиллярные сферы и др.). В обсерватории был создан труд «Новые астрономические таблицы», который содержал изложение теоретических основ астрономии и каталог положений 1018 звезд, определенных впервые после Гиппарха с точностью, остававшейся непревзойденной вплоть до наблюдений Тихо Браге. Звездный каталог, планетные таблицы, уточнения наклона эклиптики к экватору, определения длины звездного года с ошибкой в одну минуту, годичной прецессии и продолжительности тропического года имели большое значение для развития астрономии. Результатами наблюдений в обсерватории Улугбека долгое время пользовались европейские ученые.

В теоретической астрономии основное внимание уделялось уточнению кинематико-геометрических моделей «Альмагеста», устранению противоречий в теории Птолемея (в том числе с помощью более совершенной тригонометрии) и поиску нептолемеевских методов моделирования движения небесных тел. Следует упомянуть попытки согласования «Альмагеста» с моделью гомоцентрических сфер (Ибн Баджжи, Ибн Рушд, аль-Битруджи) и моделью, предложенной марагинской школой (Насирэддин ат-Туси, аш-Ширази, аш-Шатир), согласно которой «земное» прямолинейное движение участвует в движении небесных тел равноправно с равномерным круговым, что наметило тенденцию к объединению «земной» и «небесной» механик.