
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Включение цепи R, L к источнику постоянного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Примером такой цепи может служить эквивалентная схема катушки индуктивности, обладающей активным сопротивлением R и индуктивностью L. Дифференциальное уравнение такой цепи Соответствующее однородное уравнение, определяющее свободный ток: Характеристическое уравнение Lp + R = 0 имеет единственный корень p = –R/L. Тогда свободный ток можно вычислить как Ток в переходном режиме Постоянная интегрирования A определяется по начальному значению тока i. 1. Пусть цепь в момент t = 0 отключается от источника и замыкается накоротко (рис. 9.1).
После замыкания накоротко u = 0. Установившийся ток в этом случае iу = 0. Тогда полный ток Начальное условие для определения A: i(0+) = i(0–). Пусть к моменту коммутации ток в цепи был равен i(0–) = I. Следовательно, i(0+) = I. Полагая в уравнении (9.6) i = I и t = 0, находим I = A. Решение уравнения имеет вид Величина τ = L/R имеет размерность времени и называется постоянной времени цепи. За промежуток времени t ток уменьшается в e раз. Чем больше τ, тем медленнее затухает ток. Теоретически ток станет равным нулю через бесконечно большой промежуток времени, практически он становится малым за промежуток времени в несколько значений τ (рис. 9.2). Постоянная времени τ равна длине подкасательной в любой точке кривой i(t) на рис. 9.2, так как Энергия, выделяемая в виде теплоты в активном сопротивлении R, равна энергии, запасенной в магнитном поле цепи в начальный момент времени
Рис. 9.2. Кривая изменения тока в катушке индуктивности Постоянная времени τ больших катушек с сердечником может быть весьма значительной. Так, постоянная времени обмотки возбуждения крупных гидрогенераторов может иметь значение 5 с. 2. Рассмотрим процесс отключения от источника постоянного напряжения цепи, состоящей из индуктивной катушки с параметрами R и L и соединенной с ней параллельно ветви с сопротивлением R0(рис. 9.3).
Рис. 9.3. Отключение катушки индуктивности Переходный процесс описывается уравнением где До размыкания рубильника в катушке протекает ток iL(0–) = U/R. A = iL(0+) = iL(0–) = U/R. Ток в катушке Напряжение на участке с сопротивлением R0 до размыкания было равно U, а в первый момент времени после размыкания оно окажется равным Если R0 > R, например, на зажимах катушки с сопротивлением R включен вольтметр с большим сопротивлением, то при отключении цепи напряжение на вольтметре в первый момент повысится R0/R раз. Если энергия магнитного поля, запасенная в катушке достаточно велика, то вольтметр может быть сожжен. Поэтому во избежание возникновения больших перенапряжений при отключении цепей постоянного тока, обладающих большой индуктивностью, например, обмоток возбуждения генераторов, эти цепи предварительно замыкают на малое сопротивление. 3. Рассмотрим процессы при включении RL цепи на постоянное напряжение u = U = const (рис. 9.4). Ток установившегося режима iу = U/R. Общий ток в переходном режиме
Рис. 9.4. Включение катушки индуктивности на постоянное напряжение Если до включения ток был равен нулю i(0–) = 0, то при t = 0 Решение уравнения Напряжение на зажимах катушки Кривые изменения тока и напряжения на катушке показаны на рис. 9.5. 4. Рассмотрим процесс при включении цепи под синусоидальное напряжение: Ток установившегося режима
Рис. 9.5. Кривые изменения тока и напряжения Общий ток где Постоянную интегрирования A определяем из начального условия i(0–) = 0. i(0+) = i(0–) = Imsin(Ψ – j) + A = 0 Общий ток: Кривые изменения тока и напряжения изображены на рис. 9.6.
Рис. 9.6. Кривые изменения тока и напряжения при включении катушки на синусоидальное напряжение Начальное значение свободного тока зависит от начальной фазы Ψ напряжения. Наибольшее значение свободного тока, равное амплитуде Im установившегося тока, имеет место, если Ψ – j = +π/2. Наибольшее значение результирующего тока не превышает двойной амплитуды установившегося тока. Свободный ток не возникает, и сразу наступает установившийся режим при условии Ψ = j.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 943; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.39 (0.008 с.) |

 ,(9.4)где u(t) – напряжение на зажимах цепи.
,(9.4)где u(t) – напряжение на зажимах цепи. .
. . (9.5)Выражение установившегося тока iу(t), являющегося частным решением дифференциального уравнения, определяемое видом заданной функции u(t).
. (9.5)Выражение установившегося тока iу(t), являющегося частным решением дифференциального уравнения, определяемое видом заданной функции u(t). .
. Рис. 9.1. Замыкание катушки индуктивности накоротко
Рис. 9.1. Замыкание катушки индуктивности накоротко . (9.6)
. (9.6)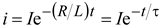 . (9.7)
. (9.7) .
.
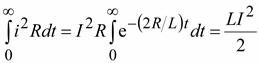 . (9.8)
. (9.8)
 ,
, .
. .(9.9)
.(9.9) .(9.10)
.(9.10) .
.
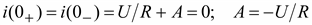 .
.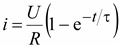 .(9.11)
.(9.11)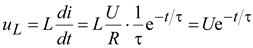 .(9.12)
.(9.12) .
. .
.
 ,
, .
. .(9.13)
.(9.13)



