
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа и мощность в цепи постоянного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника; Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:
По закону сохранения энергии: работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия В системе СИ:
ЗАКОН ДЖОУЛЯ -ЛЕНЦА При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам. Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время. В системе СИ: [Q] = 1 Дж МОЩНОСТЬ ПОСТОЯННОГО ТОКА - отношение работы тока за время t к этому интервалу времени.
В системе СИ:
Первый закон Кирхгофа.
Сколько тока втекает в узел, столько из него и вытекает. i 2 + i 3 = i 1 + i 4 Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
7. Расчет цепи методом эквивалентных структурных преобразований. Метод эквивалентных структурных преобразований. В основе различных методов преобразования электрических схем лежит понятие эквивалентности, согласно которому напряжения и токи в ветвях схемы, не затронутых преобразованием, остаются неизменными. Преобразования электрических схем применяются для упрощения расчетов. Рассмотрим наиболее типичные методы преобразования. Последовательное соединение элементов. При последовательном соединении элементов через них протекает один и тот же ток I (рис. 1.18). Согласно второму закону Кирхгофа, напряжение, приложенное ко всей цепи
Для последовательного соединения сопротивлений r1,r2...rn (рис. 1.18) с учетом (1.6) будем иметь
Ток в цепи с последовательным соединением элементов равен:
а напряжение на n-ом элементе равно
При последовательном соединении источников напряжения они заменяются одним эквивалентным источником с напряжением Uэкв, равным алгебраической сумме напряжений отдельных источников. Причем со знаком «+» берутся напряжения, совпадающие с напряжением эквивалентного источника, а со знаком «-» - несовпадающие (рис. 1.19).
Параллельное соединение элементов. Соединение групп элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным (рис. 1.20). Согласно первому Кирхгофа, ток всей цепи I равен алгебраической сумме токов в параллельных ветвях, т.е.
На основании этого уравнения с учетом (1.8) для параллельного соединения резистивных элементов получаем:
где
Токи и мощности параллельно соединенных ветвей при U=const (рис. 1.20) не зависят друг от друга и определяются по формулам:
Мощность всей цепи равна:
где rэ=1/gэ -эквивалентное сопротивление цепи. При увеличении числа параллельных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление соответственно уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность Р. Токи и мощности ранее включенных ветвей не изменяются. Рассмотрим частные случаи параллельного соединения резистивных элементов. а) параллельное соединение двух элементов
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 7606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.226 (0.007 с.) |




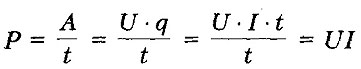


 Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда. (1.27)
(1.27) (1.28)
(1.28)
 (1.29)
(1.29) (1.30)
(1.30) (1.31)
(1.31)
 (1.32)
(1.32) -эквивалентная проводимость.
-эквивалентная проводимость.
 (1.33)
(1.33) ,
,  (1.34)
(1.34)



 (1.36)
(1.36)


