
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм имитационного моделирования цепи Маркова
Задано: a) матрица переходных вероятностей P; b) номер стартового состояния j 0; c) число временных шагов исследования процесса tk; d) число статистических экспериментов N. Требуется: вычислить оценки вероятностей нахождения процесса в различных состояниях X [ j ] в момент времени t = tk. Алгоритм 1. Создаем два массива X и Y длиной n. Заполняем массив X нулями. полагаем tk =1. 2. Полагаем t =0 и помещаем 1 в позицию j 0 массива Y, остальные элементы этого массива – нули. 3. Выполняем основной шаг алгоритма – определяем номер очередного состояния j. Прибавляем 1 к элементу Y [ j ]. Увеличиваем t на 1. 4. Повторяем шаг 3 до тех пор, пока 5. Пересчитываем X:= X + Y. 6. Повторяем шаги 2 – 5 N раз. 7. Вычисляем значения X [ j ] = X [ j ] / N, j =1,.. n, которые являются оценками среднего числа пребываний процесса в j -м состоянии. 8. Вычисляем сумму 9. Повторяем шаги 1-7 для всех
Основной шаг алгоритма Пусть в момент времени t система находится в состоянии Sk. Определим номер состояния, в которое система перейдет в момент t +1. Выделим k – ю строку матрицы P: pk = [ pk 1, pk 2 ,…, pkn ], С помощью датчика случайных чисел генерируем случайное число r (t), Иными словами, j – это номер элемента строки pk, для которого сумма Исходные данные к работе
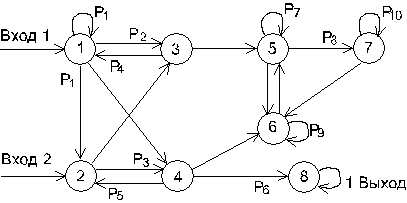
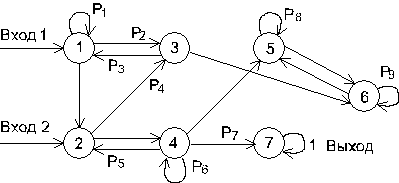
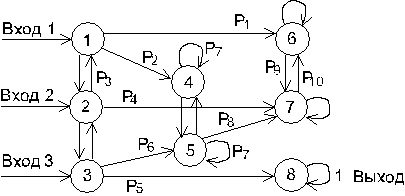
Исходные данные представлены в виде таблицы и набора схем. По указанному преподавателем номеру варианта в таблице выбирается соответствующая строка. Второй столбец таблицы указывает код схемы и стартовое состояние (например, Г1 – схема Г, старт происходит из состояния S 1). Далее указаны вероятности перехода между состояниями в десятых долях (т.е. указанное в таблице значение



Контрольные вопросы 1 Дайте определение дискретной цепи Маркова. 2 Какими свойствами обладают матрица переходных вероятностей? 3 Как рассчитываются вероятности нахождения однородной цепи Маркова в определенном состоянии через нужное число тактов? 4 Что такое начальное состояние цепи? 5 Дайте определение однородной цепи Маркова? Лабораторная работа № 2. Моделирование динамики систем на основе
Цели работы - освоить основные положения теории конечных цепей Маркова (ЦМ) с дискретным временем. - научиться составлять ЦМ для моделирования вычислительных систем и анализа динамики их функционирования.
- провести расчет характеристик производительности вычислительных систем с использованием пакета MathCad. Содержание работы 1. Изучить теоретический материал по ЦМ по учебному пособию 2. Для системы заданной в Лабораторной работе №1, провести следующие вычисления. 2.1. Структурировать матрицу 2.2. Вычислить среднее число тактов пребывания процесса в каждом из невозвратных состояний путем вычисления матрицы 2.3. На основе матрицы 2.4. Получить оценку строки матрицы 1. Выполнение шага 3 прекращается, если очередное состояние 2. Исключается шаг 8. на печать выводится результат шага 7. 3. Расчет ведется только для максимального значения 2.5. Оценить среднеквадратичное отклонение от среднего числа пребываний процесса в множестве невозвратных состояний 2.6. Оценить предельные вероятности пребывания процесса в множестве эргодических состояний. Оформление отчета по работе Отчет по лабораторной работе должен содержать: · титульный лист с указанием всех исполнителей и номера группы; · исходные данные по ЦМ – граф состояний и матрицы переходных вероятностей · матрицу средних значений · оценку строки матрицы · матрицу дисперсий · листинг модифицированной программы имитационного моделирования ЦМ с подсчетом среднего числа пребываний процесса в различных состояниях; · оценки предельных вероятностей пребывания процесса в состояниях эргодического множества: а) путем прямого возведения матрицы б) путем спектрального разложения матрицы.
Контрольные вопросы 1 Как определить какие состояния будут невозвратными? 2 Дайте определения невозвратных и эргодических состояний? 3 Как определить число среднее число пребываний цепи в каком-то невозвратном состоянии? 4 Как имитационно смоделировать фундаментальную матрицу? 5 Что такое трудоемкость процесса исполняемого цепью Маркова? 6 Что такое предельное состояние цепи Маркова? 7 Сформулируйте основные шаги алгоритма нахождения предельного состояния. Лабораторная работа № 3. Моделирование динамики систем на основе
Цели работы - освоить основные положения теории конечных цепей Маркова (ЦМ) с непрерывнымвременем. - научиться составлять и исследовать модели вычислительных систем на основе этой теории. Содержание работы · изучить теоретический материал по учебникам [1], [2], [3] или лекциям. · создать ЦМ с непрерывным временем на базе модели, рассмотренной в Лабораторных работах №1 и №2. Для этого:
· по заданному номеру варианта из таблицы в Лабораторной работе №1, взять величину · составить матрицу p (формула (3.42)). · составить уравнение Колмогорова в матричной и компонентной формах для определения динамики изменения вектора вероятностей · решить уравнение Колмогорова с заданными начальными условиями с помощью пакета MathCad. Решение вести до получения установившихся значений вектора · Вычислить установившиеся значения вектора Оформление отчета по работе Отчет по лабораторной работе должен содержать: · титульный лист с указанием всех исполнителей и номера группы; · исходные данные по ЦМ – граф состояний с указанием плотностей вероятностей переходов · матрицу p; · уравнение Колмогорова в матричном и компонентном виде и начальные условия; · график решения – все компоненты вектора · систему уравнений для вычисления установившегося значения
Контрольные вопросы 1 Дайте определение непрерывной стационарной цепи Маркова. 2 Как составляется уравнение Колмогорова по графу цепи? 3 Как в пакете MathCad получить решение уравнения Колмогорова? 4 Что такое интенсивность непрерывной цепи Маркова? 5 Как сравнивать результаты выполнения лабораторных работ №1 и №3? Сетевые модели Среди моделей этого класса выделился подход, основанный на использовании сетей специального вида, предложенный Карлом Петри в 1962 году для моделирования асинхронных информационных потоков в системах обработки данных. Эта методология, получившая название сетей Петри, была развита в последующие годы многочисленными исследователями и получила широкое распространение. Большой вклад в развитие теории сетей петри внесли отечественные ученые, в частности, математики из Новосибирского научного центра во главе с В.Е. Котовым [4]. В последние годы получила распространение теория так называемых сетей петри высокого уровня, которая изложена, например, в трехтомной работе Курта Йенсена [5]. Эта разновидность сетей Петри позволяет моделировать весьма сложные дискретные динамические системы, а их описание представлено с помощью специализированного алгоритмического языка
Математический аппарат сетей Петри обладает мощными моделирующими возможностями, и его изучение стало обязательным элементом образования инженера по информатике и вычислительной технике. Обыкновенные сети Петри
Формальное определение Сеть Петри - это математическая модель дискретных динамических систем (параллельных программ, операционных систем, ЭВМ и их устройств, сетей ЭВМ), ориентированная на качественный анализ и синтез таких систем (обнаружение блокировок, тупиковых ситуаций и узких мест, автоматический синтез параллельных программ и компонентов ЭВМ и др.). Формально в терминах теории систем [4] с еть Петри (Petri Net – PN) - это набор элементов (кортеж)
В этом определении
Множества позиций и переходов не пересекаются:
где M0 - начальная маркировка позиций: Функция инцидентности может быть представлена в виде 1) 2) Эти функции, в общем случае зависящие от времени, могут быть представлены матрицами инцидентности
Из вершины - позиции Множество всех позиций Аналогично из каждой вершины перехода Множество всех переходов Каждая позиция
Начальная маркировка Динамика поведения моделируемой системы описывается в терминах функционирования сетей Петри. Как было сказано, сеть функционирует в дискретном времени
Смена маркировок (начиная с
т.е. если каждая входная позиция для данного перехода В результате срабатывания перехода
i =1,..., n, j =1,..., m, Иными словами, переход t изымает из каждой своей входной позиции число фишек, равное кратности входных дуг и посылает в каждую свою выходную позицию число фишек, равное кратности выходных дуг. Если может сработать несколько переходов, то срабатывает один, любой из них. Функционирование сети останавливается, если при некоторой маркировке (тупиковая маркировка) ни один из ее переходов не может сработать. При одной и той же начальной маркировке сеть Петри может порождать, в силу недетерминированности ее функционирования, различные последовательности срабатывания ее переходов. Эти последовательности образуют слова в алфавите T. множество всевозможных слов, порождаемых сетью Петри, называют языком сети Петри. Две сети Петри эквивалентны, если порождают один и тот же язык. В отличие от конечных автоматов, в терминах которых описываются глобальные состояния систем, сети Петри концентрируют внимание на локальных событиях (переходах), локальных условиях (позициях) и локальных связях между событиями и условиями. Поэтому в терминах сетей Петри более адекватно, чем с помощью автоматов, моделируется поведение распределенных асинхронных систем.
Графы сетей Петри Формальное определение сети Петри, изложенное выше, полностью определяет ее функционирование. Однако при решении конкретных инженерных задач удобнее и нагляднее графическое представление этих сетей. Поэтому ниже функционирование сетей Петри изложено с позиции теории графов. Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф сети Петри. Этот граф содержит: - позиции (места), обозначаемые кружками; - переходы, обозначаемые планками; - ориентированные дуги (стрелки), соединяющие позиции с переходами и переходы с позициями. Кратные дуги обозначаются несколькими параллельными дугами. Благодаря наличию кратных дуг сеть Петри есть мультиграф. Благодаря двум типам вершин граф называется двудольным. Поскольку дуги имеют направление, граф является ориентированным. Пример такого мультиграфа показан на рисунке 2.1.
р исунок 2.1 Пример сети Петри
Для сети, изображенной на этом рисунке, матрицы инцидентности имеют вид:
Начальная маркировка, как видно из рисунка 2.1, Нетрудно видеть, что матричное и графовое представления взаимно однозначно соответствуют друг другу. В случае большой кратности дуг эту кратность можно указывать цифрами на соответствующей дуге.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.234.62 (0.104 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
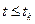 .
.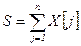 и величины
и величины 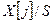 , которые представляют собой оценки вероятностей пребывания процесса в каждом состоянии. Выводим время
, которые представляют собой оценки вероятностей пребывания процесса в каждом состоянии. Выводим время 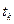 и вектор X на печать и на график.
и вектор X на печать и на график.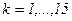 .
.
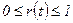 с равномерным законом распределения.Тогда номер состояния j определится условием:
с равномерным законом распределения.Тогда номер состояния j определится условием: 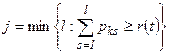
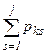 при возрастании j от 1 до n впервые не меньше r (t).
при возрастании j от 1 до n впервые не меньше r (t).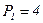 означает, что
означает, что  ). Этими вероятностями помечены дуги на схеме. Некоторые дуги не помечены – соответствующие вероятности определяются из условия, что сумма вероятностей на дугах, отходящих от каждого узла, равна единице. Следующая группа столбцов задает трудоемкости отдельных процессов
). Этими вероятностями помечены дуги на схеме. Некоторые дуги не помечены – соответствующие вероятности определяются из условия, что сумма вероятностей на дугах, отходящих от каждого узла, равна единице. Следующая группа столбцов задает трудоемкости отдельных процессов 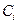 в секундах. В последнем столбце указаны величины
в секундах. В последнем столбце указаны величины 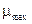 (1/с), которая используется в лабораторной работе №3
(1/с), которая используется в лабораторной работе №3

 , выделить множества невозвратных и эргодических состояний
, выделить множества невозвратных и эргодических состояний 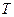 и
и  . Выписать матрицы
. Выписать матрицы 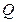 ,
,  ,
, 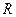 .
.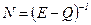 .
.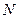 вычислить среднюю трудоемкость вычислительного процесса
вычислить среднюю трудоемкость вычислительного процесса 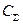 .
.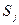 относится к эргодическому множеству:
относится к эргодическому множеству: 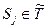 .
. .
.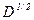 , где
, где  и соответствующее среднеквадратичное отклонение трудоемкости вычислений от среднего
и соответствующее среднеквадратичное отклонение трудоемкости вычислений от среднего 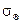 .
.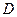 и оценку среднеквадратичного отклонения трудоемкости sQ;
и оценку среднеквадратичного отклонения трудоемкости sQ;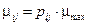 .
.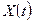 . Задать начальные условия исходя из заданного стартового состояния системы.
. Задать начальные условия исходя из заданного стартового состояния системы.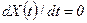 с учетом условия
с учетом условия 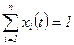 . Сравнить решение с результатом п. 3.
. Сравнить решение с результатом п. 3.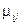 ;
;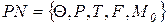 . (2.1)
. (2.1)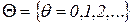 - множество дискретных моментов времени;
- множество дискретных моментов времени; - непустое множество элементов сети, называемых позициями (местами);
- непустое множество элементов сети, называемых позициями (местами); - непустое множество элементов сети, называемых переходами.
- непустое множество элементов сети, называемых переходами.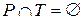 .
.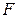 - функцияинцидентности,
- функцияинцидентности,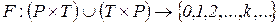 , (2.2)
, (2.2) - кратность дуги.
- кратность дуги.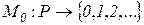 .
.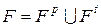 и фактически задает два отображения:
и фактически задает два отображения: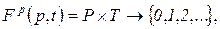 т.е. для каждой позиции указываются связанные с ней переходы (с учетом их кратности);
т.е. для каждой позиции указываются связанные с ней переходы (с учетом их кратности); т.е. для каждого перехода указываются связанные с ним позиции (также с учетом кратности).
т.е. для каждого перехода указываются связанные с ним позиции (также с учетом кратности).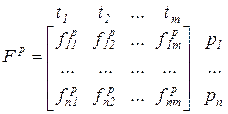 , (2.3)
, (2.3)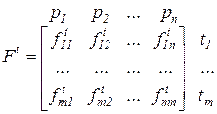 . (2.4)
. (2.4)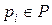 ведет дуга в вершину - переход
ведет дуга в вершину - переход  тогда и только тогда, когда
тогда и только тогда, когда 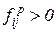 . В этом случае говорят, что
. В этом случае говорят, что  - выходной переход позиции
- выходной переход позиции 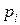 .
.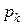 для которых
для которых 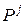 . Иными словами,
. Иными словами, 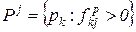 .
.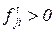 . При этом говорят, что
. При этом говорят, что 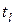 , для которых
, для которых 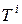 . Таким образом,
. Таким образом, 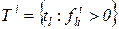 . При
. При  , часто отображаемый соответствующим числом точек (фишек) внутри позиции (см. рис. 2.1). Вектор
, часто отображаемый соответствующим числом точек (фишек) внутри позиции (см. рис. 2.1). Вектор 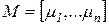 называют маркировкой (разметкой) сети Петри. Каждая маркировка это отображение
называют маркировкой (разметкой) сети Петри. Каждая маркировка это отображение . (2.5)
. (2.5)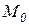 определяет стартовое состояние сети Петри.
определяет стартовое состояние сети Петри.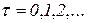 в асинхронном режиме, переходя от одной маркировки к другой.
в асинхронном режиме, переходя от одной маркировки к другой. выполняется условие
выполняется условие 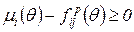 , (2.6)
, (2.6) 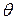 маркировка
маркировка  сменяется маркировкой
сменяется маркировкой 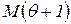 по правилу:
по правилу: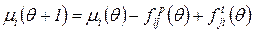 , (2.7)
, (2.7)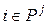 ,
, 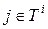 .
.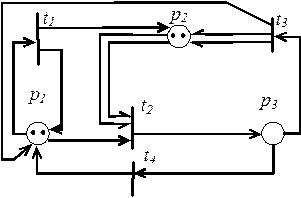
 ,
, 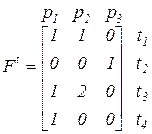 .
.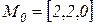 .
.


