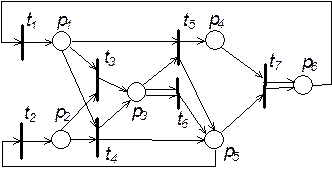Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые обобщения сетей Петри
Рассмотренное в разделах 2.1.1 – 2.1.3 базовое определение сети Петри позволяет моделировать широкий класс дискретных систем. Однако в ряде случаев этих возможностей оказывается недостаточно, поэтому вводят обобщения этих сетей, которые обладают расширенными возможностями моделирования. Упомянем некоторые из них. Ингибиторные сети (ИСП, IPN) – это сети Петри, для которых функция инцидентности имеет вид
р исунок 2.3 Фрагмент СП с ингибиторной дугой
Правила срабатывания переходов в ингибиторной сети модифицируются следующим образом. Переход
т.е. по сравнению с условием (2.6) введено дополнительное условие: позиция Сети с приоритетами. при определении сети Петри отмечалась недетерминированность ее работы: если имеется возможность срабатывания нескольких переходов, то срабатывает любой из них. При моделировании реальных систем могут сложиться ситуации, когда последовательность срабатываний необходимо регламентировать. Это можно сделать, введя множество приоритетов
а) б) Рисунок 2.4 Сеть Петри с заданными приоритетами (а), эквивалентная цепь Маркова при вероятностном срабатывании переходов (б)
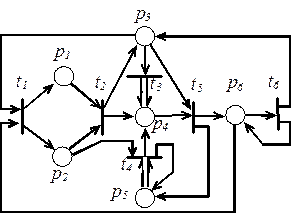
Сети со случайными срабатываниями переходов. В описанной выше ситуации, когда имеется возможность срабатывания нескольких переходов Пусть на рисунке 2.4 а) вероятность срабатывания перехода Иерархические сети Петри представляют собой многоуровневые структуры, в которых выделяются сети различного уровня. Они позволяют моделировать различные многоуровневые (иерархические) системы. В отличие от обыкновенных сетей Петри, в иерархических сетях имеются два типа переходов: простые и составные. Простые переходы ничем не отличаются от рассмотренных ранее, а составные переходы содержат внутри себя сеть Петри более низкого уровня. Формально они состоят из входного («головного») и выходного («хвостового») переходов, между ними находится некоторая сеть Петри, которая, в свою очередь, также может быть иерархической. Пример иерархической сети
Рисунок 2.5 Иерархическая сеть Петри
Иерархическая сеть функционирует, как и обыкновенная СП, переходя от одной маркировки к другой и обмениваясь фишками (в том числе между сетями различного уровня). Исключение составляют правила работы составных переходов. Срабатывание составных переходов является не единовременным событием, как в обыкновенных СП, а составным действием. Поэтому говорят не о срабатывании составного перехода, а о его работе. На каждом шаге дискретного времени
Ниже приведено дерево маркировок сетей Мы видим, что на шаге Отметим также, что описанный процесс напоминает выполнение подпрограммы при программировании на алгоритмических языках. Срабатывание перехода
Рисунок 2.6 Схема работы иерархической сети Петри 2.1.6 Инварианты сетей Петри Структура сетей Петри может обеспечивать при работе сети постоянство некоторых функций от маркировок сети. Такие функции называют инвариантами сетей Петри. Вычисление инвариантов может оказаться полезным при исследовании свойств моделируемых систем (например, при верификации и тестировании программ, анализе бизнес-процессов и др.). Различают инварианты позиций и инварианты переходов. Для того, чтобы пояснить смысл этих терминов, введем в рассмотрение
каждый элемент которой 1. Инварианты позиций. Припишем каждой позиции
Рассмотрим
где Представим матрицу
где
Отсюда следует, что условие (4.10) при
Пусть для простоты имеются две такие строки с номерами
Таким образом, вектор
и в силу (2.11) обеспечивается выполнение условия (2.10). Подсчитаем теперь приращение числа фишек в позициях Таким образом, сумма Построенный описанным образом вектор 2. Инварианты переходов. По аналогии с предыдущим разделом припишем каждому переходу
Рассмотрим
где Аналогично сказанному выше, можно убедиться в том, что условие (2.12) выполняется только в том случае, когда среди столбцов матрицы Проанализируем теперь, как будет изменяться маркировка сети при последовательном срабатывании переходов Вектор
Приведенные рассуждения легко обобщаются и на случай, когда число линейно зависимых строк (и столбцов) в матрице Из сказанного вытекает также, что задача нахождения инвариантов сети Петри решается неоднозначно. Так, например, умножив веса Отметим один частный случай. Если для некоторой сети Петри существует вектор-инвариант позиций
Такая сеть Петри, как было сказано выше, называется консервативной. Пример. Рассмотрим сеть Петри, изображенную на рисунке 2.1 и составим для нее матрицу
Легко видеть, что в этой матрице первая и третья строки линейно зависимы, причем достаточно взять веса Рассмотрим теперь столбцы матрицы
Это означает, что при последовательном срабатывании переходов Лабораторная работа № 4 Моделирование систем с помощью
Цель работы: - освоить основные формализмы обыкновенных сетей Петри (PN). - научиться составлять формальное описание PN. - разработать программу моделирования динамики маркировок и составления слов свободного языка обыкновенных сетей Петри. - провести исследования заданной сети с помощью разработанной программы. Содержание работы 1) Изучить теоретический материал по учебнику [1], [2] или лекциям. Получить свой вариант задания 2) Составить программу, моделирующую изменение маркировок и построение свободного языка обыкновенной сети Петри. 3) Для заданного варианта задания: 1. Составить список позиций и переходов, матрицы инцидентности F (p,t) и F (t,p) и начальную маркировку для указанного варианта схемы СП. 2. Для начальной маркировки PN, указанной в таблице, составить дерево разметок на глубину до 5 шагов или до общего числа маркировок, равного 100. При обнаружении повторяющихся маркировок они помечаются значками Mpi, где i - номер обнаруженной повторяющейся маркировки, а построение дерева продолжается только из одной из них. Циклические маркировки, т.е. повторяющиеся на одном пути в дереве, обозначаются Mci. Тупиковые маркировки обозначаются Mti.
3. Выписать все полученные слова свободного языка PN, начиная с пустого слова. Аналогично п.2 указать повторения, циклы и тупики. 4. Оценить свойства PN: ограниченность, консервативность, безопасность, живость.
Оформление работы Оформленный отчет по лабораторной работе должен содержать: - титульный лист с указанием фамилий исполнителей, группы и номера варианта; - исходную схему с начальной маркировкой; - матрицы инцидентности; - дерево маркировок; - словарь свободного языка PN; - анализ свойств рассматриваемой PN; - листинг программы. Таблица исходных данных
Исходные схемы PN
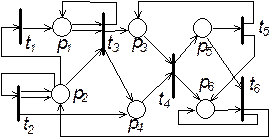

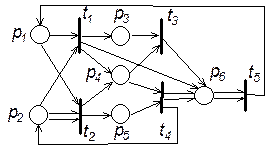
Контрольные вопросы 1. Какие элементы содержит сеть Петри? 2. Сформулируйте правило срабатывания сети Петри. 3. По какому правилу меняются маркировки сети при срабатывании одного перехода? 4. Как построить дерево маркировок сети до определенной глубины? 5. Дайте определение ограниченности позиции в сети. 6. Какие основные свойства переходов вы знаете? 7. Что такое множество достижимости сети Петри? Лабораторная работа № 5 Моделирование систем с помощью
Цель работы: - освоить основные формализмы ингибиторных сетей Петри (IPN). - научиться составлять формальное описание IPN. - разработать программу моделирования динамики маркировок и составления слов свободного языка ингибиторных сетей Петри. - провести исследования основных свойств заданной сети с помощью разработанной программы. Содержание работы 1) Изучить описание ингибиторных связей и особенности функционирования IPN по учебникам [1], [2] или по лекциям. 2) Модернизировать разработанную в лабораторной работе №4 программу, введя в нее описание и механизм работы IPN. 3) Провести исследование заданного варианта IPN аналогично исследованию в лабораторной работе №4 (пункты 1-4). Сравнить дерево маркировок и свободный язык IPN с аналогичными характеристиками обыкновенной PN. Исходные данные В соответствии с указанным номером варианта, в схему, использованную в лабораторной работе №4, внести следующие изменения: - изменить начальную маркировку в соответствии с приведенной ниже таблицей; - заменить указанные в последнем столбце таблицы дуги на ингибиторные. Оформление работы Оформленный отчет по лабораторной работе должен содержать: - титульный лист с указанием фамилий исполнителей, группы и номера варианта; - исходную схему с начальной маркировкой; - матрицы инцидентности; - дерево маркировок; - словарь свободного языка PN; - анализ свойств рассматриваемой PN; - листинг программы. Таблица исходных данных
Контрольные вопросы 8. Какие элементы содержит сеть Петри? 9. Сформулируйте правило срабатывания сети Петри. 10. По какому правилу меняются маркировки сети при срабатывании одного перехода? 11. Как построить дерево маркировок сети до определенной глубины? 12. Дайте определение ограниченности позиции в сети. 13. Какие основные свойства переходов вы знаете? 14. Что такое множество достижимости сети Петри?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 79; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.161.222 (0.143 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , т.е. она дополнена специальной функцией инцидентности
, т.е. она дополнена специальной функцией инцидентности 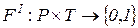 , которая вводит ингибиторные дуги для тех пар
, которая вводит ингибиторные дуги для тех пар 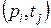 , для которых
, для которых 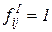 . Ингибиторные дуги связывают только позиции с переходами, эти дуги на рисунках заканчиваются не стрелками, а кружочками (рисунок 2.3). Кратность этих дуг всегда равна 1.
. Ингибиторные дуги связывают только позиции с переходами, эти дуги на рисунках заканчиваются не стрелками, а кружочками (рисунок 2.3). Кратность этих дуг всегда равна 1.
 может сработать при маркировке M, если для всех связанных с ним позиций
может сработать при маркировке M, если для всех связанных с ним позиций 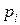 и
и 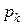
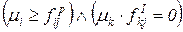 , (2.9)
, (2.9) и
и 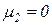 .
.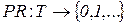 и приписав каждому из переходов
и приписав каждому из переходов 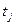 соответствующее целочисленное значение приоритета
соответствующее целочисленное значение приоритета 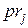 . Тогда правило срабатывания переходов модифицируется: если на некотором такте работы сети
. Тогда правило срабатывания переходов модифицируется: если на некотором такте работы сети  имеется возможность для срабатывания нескольких переходов, то срабатывает тот из них, который имеет наивысший приоритет. Так, из двух готовых к срабатыванию переходов
имеется возможность для срабатывания нескольких переходов, то срабатывает тот из них, который имеет наивысший приоритет. Так, из двух готовых к срабатыванию переходов 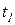 и
и 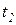 . на рисунке 2.4 а первым должен сработать переход
. на рисунке 2.4 а первым должен сработать переход 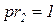 , поскольку приоритет перехода
, поскольку приоритет перехода  , т.е. ниже.
, т.е. ниже.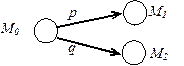
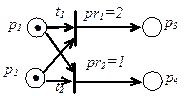
 , их приоритет можно задавать вероятностями срабатывания каждого их переходов
, их приоритет можно задавать вероятностями срабатывания каждого их переходов 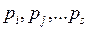 , причем
, причем  . Тогда исходная маркировка
. Тогда исходная маркировка 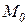 приведет на следующих шагах работы сети к набору маркировок
приведет на следующих шагах работы сети к набору маркировок 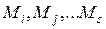 , каждая из которых будет помечена соответствующей вероятностью. Отождествив маркировки с состоянием сети и положив, что вероятности не зависят от работы сети в предыдущие такты, мы получим цепь Маркова, описывающую вероятностное поведение системы.
, каждая из которых будет помечена соответствующей вероятностью. Отождествив маркировки с состоянием сети и положив, что вероятности не зависят от работы сети в предыдущие такты, мы получим цепь Маркова, описывающую вероятностное поведение системы.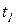 равна p, а вероятность срабатывания
равна p, а вероятность срабатывания 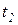 равна
равна 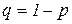 . Тогда обозначив маркировки
. Тогда обозначив маркировки 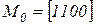 ,
,  ,
, 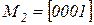 , получим цепь Маркова (рисунок 2.4 б).
, получим цепь Маркова (рисунок 2.4 б). , в которой имеется составной переход
, в которой имеется составной переход 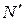 , показан на рисунке 4.5. Составной переход
, показан на рисунке 4.5. Составной переход 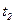 имеет «голову»
имеет «голову»  и «хвост»
и «хвост» 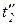 , между которыми заключена сеть
, между которыми заключена сеть 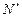 , состоящая из позиций
, состоящая из позиций 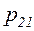 -
-  и переходов
и переходов  -
- 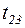 .
.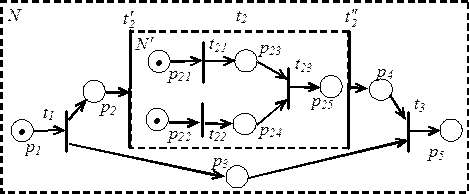
 составной переход может находиться в одном из двух состояний – пассивном и активном. Начальное состояние всех переходов – пассивное. Составной переход может быть активирован, в момент времени
составной переход может находиться в одном из двух состояний – пассивном и активном. Начальное состояние всех переходов – пассивное. Составной переход может быть активирован, в момент времени  и
и  происходит работа составного перехода
происходит работа составного перехода 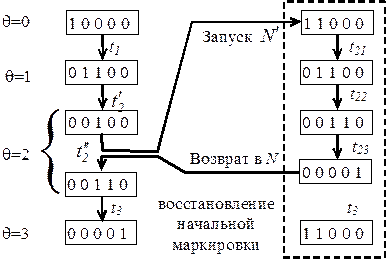
 -матрицу
-матрицу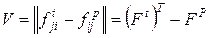 ,
, показывает разность между числом поступивших фишек -
показывает разность между числом поступивших фишек - 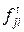 и числом изъятых
и числом изъятых 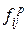 , т.е. изменение маркировки позиции
, т.е. изменение маркировки позиции 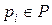 при срабатывании перехода
при срабатывании перехода 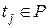 . В силу того, что
. В силу того, что 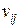 также целые. В зависимости от знака
также целые. В зависимости от знака  ), либо уменьшается (
), либо уменьшается (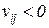 ), либо остается неизменным (
), либо остается неизменным ( ).
).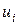 , который может принимать целочисленные значения – положительные, отрицательные или нулевые. Эти веса образуют
, который может принимать целочисленные значения – положительные, отрицательные или нулевые. Эти веса образуют 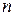 -вектор-строку
-вектор-строку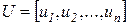 .
.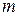 -вектор-строку
-вектор-строку 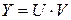 и определим условия, при которых этот вектор является нулевым, т.е.
и определим условия, при которых этот вектор является нулевым, т.е.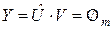 (2.10)
(2.10)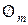 -
- 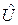 - ненулевой
- ненулевой 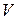 в виде
в виде 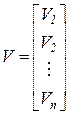 ,
,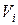 -вектор-строка. Тогда условие (4.10) может быть представлено в виде
-вектор-строка. Тогда условие (4.10) может быть представлено в виде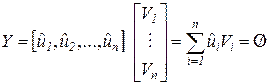 .
. может выполняться только в том случае, если среди строк
может выполняться только в том случае, если среди строк 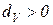 .
. и
и 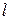 -
- 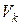 и
и  , которые соответствуют в матрице
, которые соответствуют в матрице  , и пусть соответствующие веса не равны нулю:
, и пусть соответствующие веса не равны нулю: 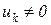 ,
, 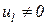 . Веса остальных позиций положим равными нулю:
. Веса остальных позиций положим равными нулю: 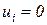 при
при 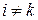 ,
, 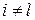 . В силу линейной зависимости строк
. В силу линейной зависимости строк  и
и 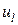 можно подобрать таким образом, что
можно подобрать таким образом, что ;
; 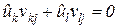 ,
, 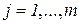 . (2.11)
. (2.11)
 . Пусть до срабатывания перехода
. Пусть до срабатывания перехода 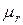 и
и 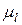 . После срабатывания
. После срабатывания 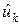 и
и 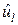 стали равными,
стали равными, 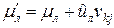 ,
, 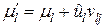 , а их сумма
, а их сумма 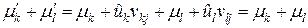 осталась прежней в силу (2.11).
осталась прежней в силу (2.11).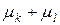 при учете введенных весов позиций
при учете введенных весов позиций 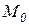 .
.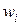 , который может принимать целочисленные значения любого знака. Эти веса сведем в
, который может принимать целочисленные значения любого знака. Эти веса сведем в 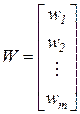 .
.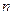 -вектор-столбец
-вектор-столбец 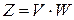 и определим условия, при которых этот вектор является нулевым, т.е.
и определим условия, при которых этот вектор является нулевым, т.е.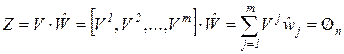 , (2.12)
, (2.12)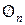 -
- 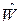 - ненулевой
- ненулевой 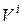 -
-  -й
-й 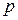 и
и 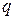 , которые соответствуют переходам
, которые соответствуют переходам 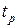 и
и  , и пусть соответствующие веса не равны нулю,
, и пусть соответствующие веса не равны нулю, 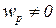 ,
, 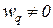 . Остальные веса положим нулевыми:
. Остальные веса положим нулевыми: 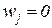 при
при 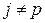 ,
, 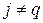 . В силу линейной зависимости векторов
. В силу линейной зависимости векторов 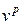 и
и  можно подобрать веса
можно подобрать веса 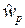 и
и 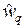 таким образом, чтобы выполнялось условие (2.12).
таким образом, чтобы выполнялось условие (2.12). . После срабатывания
. После срабатывания 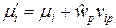 а после срабатывания
а после срабатывания  . Таким образом, после последнего срабатывания переходов
. Таким образом, после последнего срабатывания переходов  .
.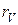 . Величина
. Величина 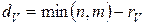 называется дефектом матрицы
называется дефектом матрицы 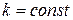 , мы получим другой вектор-инвариант
, мы получим другой вектор-инвариант 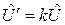 , который обладает теми же свойствами, что и
, который обладает теми же свойствами, что и 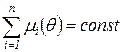 ,
, 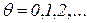 .
.
 ,
, 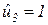 ,
,  . При этом получим вектор-инвариант по позициям
. При этом получим вектор-инвариант по позициям  , следовательно, сумма фишек в позициях
, следовательно, сумма фишек в позициях 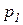 и
и 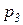 постоянна при срабатывании любого перехода:
постоянна при срабатывании любого перехода: 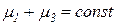 , в чем легко убедиться, проанализировав дерево маркировок на рисунке 2.2.
, в чем легко убедиться, проанализировав дерево маркировок на рисунке 2.2.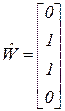 .
. (в любом порядке) маркировка сети повторяется. Это также видно на рисунке 2.2. Но это не единственный инвариант по переходам. Цепочка срабатываний переходов
(в любом порядке) маркировка сети повторяется. Это также видно на рисунке 2.2. Но это не единственный инвариант по переходам. Цепочка срабатываний переходов  (t 1, t 1, t 2 , t 4) в любом порядке приводит к той же маркировке.
(t 1, t 1, t 2 , t 4) в любом порядке приводит к той же маркировке.